
- •15.Найімовірніше число появи випадкової події (мода)
- •16. Локальна теорема
- •17. Інтегральна теорема
- •Властивості функції Лапласа
- •18. Використання інтегральної теореми
- •19. Формула Пуассона
- •20.Дискретні та неперервні випадкові величини. Закони розподілу їх імовірностей
- •21. Функція розподілу ймовірностей (інтегральна функція) та її властивості
- •22. Щільність імовірностей (диференціальна функція) f (X) і її властивості
- •23. Математичне сподівання
- •24. Властивості математичного сподівання
- •26. Дисперсія та середнє квадратичне відхилення
- •27. Властивості дисперсії
- •28. Початкові та центральні моменти
- •30Система двох дискретних випадкових величин (X, y) та їх числові характеристики
- •37.Функції одного випадкового аргументу
- •38. Математичне сподівання Функції одного випадкового аргументу
- •4.2. Знаходження f (z), f (z), якщо
- •40. Числові характеристики функції n випадкових аргументів
- •41. Біноміальний закон розподілу ймовірностей
- •45. Геометричний закон розподілу ймовірностей
- •42. Рівномірний закон розподілу ймовірностей. Рівномірний закон розподілу
- •11.1. Числові характеристики
- •43. Нормальний закон розподілу
- •46.. Розподіл 2 (хі-квадрат)
- •47.Математичне сподівання і дисперсія при нормальному розподілу.
- •Різниця
4.2. Знаходження f (z), f (z), якщо
Оскільки пряма Y = ZХ ділить площину хОу на дві непересічені області, зображені на рис. 82.

Рис. 82
В
області D1
виконується випадкова подія
![]() і
в області
і
в області
![]() .
Отже, імовірність події
.
Отже, імовірність події
![]() дорівнюватиме сумі ймовірностей двох
несумісних випадкових подій, що зможуть
відбутися або в області
дорівнюватиме сумі ймовірностей двох
несумісних випадкових подій, що зможуть
відбутися або в області
![]() ,
або в області
,
або в області
![]() :
:
![]() .
.
Отже,
![]() (211)
(211)
або
![]() (212)
(212)
Щільність імовірностей

Остаточно маємо:
![]() (213)
(213)
Якщо Х і Y є незалежними, то
![]() . (214)
. (214)
40. Числові характеристики функції n випадкових аргументів
1. Математичне сподівання.
А. М (Х + Y) = М (Х) + М (Y). (218)
Доведення. Нехай Х і Y є неперервними випадковими величинами. Тоді

Оскільки
![]() ,
то
,
то
![]()
Висновок 1.
М (АХ + ВY + С) = АМ (Х) + ВМ (Y) + С. (219)
тут А, В, С — деякі сталі.
!
Доведення.

оскільки
![]()
Висновок 2. . (220)
. (220)
Б. Якщо випадкові величини є між собою незалежними, то
М (ХY) = М (Х) М (Y). (221)
Доведення.
![]()
(оскільки для незалежних випадкових величин f (x, y) = f (x) f (y)).
41. Біноміальний закон розподілу ймовірностей
Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
![]() k
= 0, 1, 2, 3, ...,
n. (234
а)
k
= 0, 1, 2, 3, ...,
n. (234
а)
У табличній формі цей закон набирає такого вигляду:
|
0 |
1 |
2 |
3 |
... |
n |
|
|
|
|
|
|
|
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:
![]() .
.
Побудуємо ймовірнісну твірну функцію для цього закону
![]() .
.
Отже, імовірнісна твірна функція для біноміального закону
![]() . (234
b)
. (234
b)
Знайдемо основні числові характеристики для цього закону:
![]()
![]() . (235)
. (235)


 ;
;
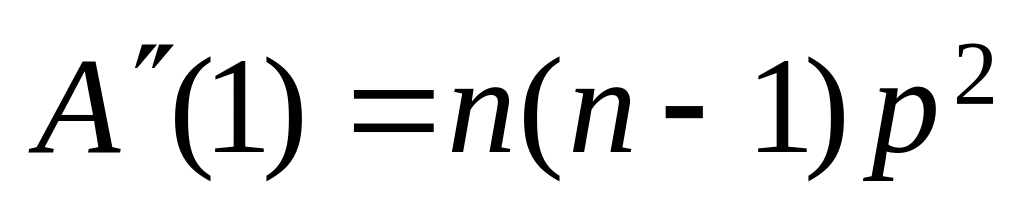 ;
;
![]()
![]() ; (236)
; (236)
![]() . (237)
. (237)
Приклад
1. У партії
однотипних деталей стандартні становлять
95%. Навмання з партії беруть 400 деталей.
Визначити
М
(Х),
D (X),
(Х)
для дискретної випадкової величини Х
— появи числа стандартних деталей серед
400 навмання взятих.Розв’язання.
Цілочислова
випадкова величина Х
має біноміальний закон розподілу
ймовірностей, яка може набувати значення
Х
= k
= 0, 1, 2, ..., 400.Імовірності можливих значень
обчислюються за формулою Бернуллі:
![]() ,
де р
= 0,95 — імовірність появи стандартної
деталі, q
= 1 – p
=1 – 0,95 = 0,05 — імовірність появи
нестандартної деталі.Згідно з (235), (236),
(237), маємо:
,
де р
= 0,95 — імовірність появи стандартної
деталі, q
= 1 – p
=1 – 0,95 = 0,05 — імовірність появи
нестандартної деталі.Згідно з (235), (236),
(237), маємо:
![]() =
400
0,95 = 380;
=
400
0,95 = 380;
![]() =
400
0,95
0,05 = 19;
=
400
0,95
0,05 = 19;
![]() =
=![]()
4,36.
4,36.
45. Геометричний закон розподілу ймовірностей
Інколи спроби здійснюють до першої появи випадкової події. Число проведених спроб буде цілочисловою випадковою величиною. Цілочислова випадкова величина Х має геометричний закон розподілу, якщо ймовірності її можливих значень
![]() ,
k
= 1, 2, 3, …, n. (243)
,
k
= 1, 2, 3, …, n. (243)
Тут p — імовірність появи випадкової події в кожній спробі — є величиною сталою, q = 1 – p.
У табличній формі геометричний закон розподілу такий:
|
1 |
2 |
3 |
4 |
... |
|
|
|
|
|
... |
При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії, тому й закон розподілу називають геометричним:
![]()
Побудуємо ймовірнісну твірну функцію
![]() .
.
Ураховуючи,
що
![]() ,
дістаємо
,
дістаємо
![]()
Оскільки
![]() ,
то
,
то
![]() ;
;
![]() . (244)
. (244)
Числові характеристики для цього закону:
1.
![]()
![]() ;
;
![]() . (245)
. (245)
2.
![]()
![]() ;
;
![]() .
.
![]() ; (246)
; (246)
![]() . (247)
. (247)
Серед дискретних випадкових величин лише геометричному закону притаманна властивість відсутності післядії. Це означає, що ймовірність появи випадкової події в k-му експерименті не залежить від того, скільки їх з’явилося до k-го, і завжди дорівнює p.
Приклад 5. Гральний кубик підкидається до першої появи цифри 6. Визначити М (Х), D (X), (Х) для випадкової величини Х числа здійснюваних підкидань.
Розв’язання.
Випадкова величина Х
є цілочисловою, що має геометричний
закон розподілу ймовірностей. За умовою
задачі: p = ![]() ;
q =
;
q = ![]() .
.
Скориставшись (245), (246), (247), дістанемо:
 ;
;
 ;
;
![]() .
.
