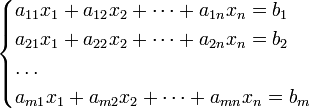N10 Метрические соотношения в Rn

Определение. Если каждой паре векторов из пространства Rⁿ поставлено в соответствие действительное число , так, что для любых из Rⁿ и любого действительного числа справедливы следующие равенства:

1. 

1. 

2. 

3. при , , — нулевой вектор,

то говорят, что в пространстве Rⁿ определено скалярное произведение .

Пространство арифметических векторов Rⁿ с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают Eⁿ.

Свойства скалярного произведения. Неравенство Коши-Буняковского

Теорема (неравенство Коши-Буняковского). Для любых векторов из пространства Rⁿ справедливо следующее неравенство .

Метрические соотношения в Rⁿ

Определение. Число называется длиной вектора ; число — расстоянием между векторами и ; угол , косинус которого — углом между векторами и .

Если в Rⁿ скалярное произведение определено формулой , то для любых , из Rⁿ справедливо:

Ортогональность, ортогональные системы, ортонормированные базисы

Определение. Векторы и из пространства Rⁿ называются ортогональными, если

Определение. Система векторов из пространства Rⁿ называется ортогональной, если векторы системы попарно ортогональны.

Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.

Определение. Система векторов из пространства Rⁿ называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.

Определение. Базис пространства Rⁿ называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.

В пространстве Rⁿ в естественном скалярном произведении естественный базис — ортонормированный базис.

N11

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].

С истема (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Р ешение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

 Рассмотрим матричное уравнение

A · X = B ,

где A — квадратная невырожденная ( det A ≠ 0 ) матрица порядка n , B — матрица размера n × m и X — неизвестная матрица.

Так как матрица A — невырожденная, то существует обратная матрица A⁻¹ . Умножим обе части уравнения слева (операция умножения матриц некоммутативна!) на матрицу A⁻¹ . По определению обратной матрицы, получим

( A−1 · A ) · X = A−1 · B       E · X = A−1 · B      X = A−1 · B .

Таким образом, искомое решение матричного уравнения определяется формулой

X = A−1 · B

Обратите внимание на то, что количество строк матрицы B должно быть равно порядку матрицы A .

N12

Правило Крамера:

Правило крамера Теорема Крамера: Система из n уравнений с n неизвестными: (1)

в случае, когда детерминант матрицы системы отличен от нуля, имеет решение, и притом только одно. Это реше­ние находится по формулам

xⁱ=ⁱ/ (для всех i=1,...,n) (2), где через ⁱ обозначен детерминант матрицы системы, а через  детерминант матрицы, получаемой из матрицы системы заменой i-го столбца столбцом свободных чле­нов, т.е.:

Для доказательства возьмем расширенную матрицу системы А* и припишем к ней сверху произвольную ее строку. Пусть номер этой строки j. В результате получа­ется квадратная матрица А порядка n+1. В этой мат­рице две одинаковые строки, и потому:

С другой стороны, мы можем вычислить detA по определению.

Итак,

(n||i=1)(–1)ⁱ⁺¹a_i^jM_i+(1)ⁿ⁺¹⁺¹det Ab_j =0. Здесь через M_i обозначен детерминант матрицы, получае­мой из расширенной матрицы A* вычеркиванием i-го столбца. =>, учитывая, что =det A0, мы можем написать

Если внести множитель под знак суммы, это равенство примет вид

где:

Так определенный набор чисел х¹,...,xⁿ, как мы видим, удовлетворяет j-му уравнению системы. Существенно, что числа x¹,..., xⁿ не зависят от j и потому удовлетворяют всем уравнениям системы, т.е. являются её решением. Существование решения доказано. Мы приведём xⁱ к нужному виду, если переставим в А последний столбец b на 1-е место, т.е. поменяем его местами последовательно со столбцами с номерами n, n–1,...,i+1. Всего нужно n–i перестановок. Поэтому x¹=((–1)ⁿ⁺ⁱ(–1)^n–iⁱ)/= ⁱ/. Это и есть требуемый вид для хⁱ. Нам осталось доказать единственность полученного решения. Сделаем это от противного. Пусть нашлось два решения системы: a¹,...,aⁿ и ¹,..., ⁿ. Пользуясь операциями со столбцами, мы можем записать систему в виде x¹a₁+...+xⁿa_n=b,где a₁,...,a_n – столб­цы матрицы системы, b – столбец свободных членов. Результат подстановки решений (4) в систему имеет вид ¹a₁+...+ⁿa_n=b

¹a₁+...+ⁿa_n=b. Вычитая почленно второе равенство из первого, мы по­лучаем (¹–¹)a₁+...+(ⁿ–ⁿ)a_n=0 Если решения не совпадают, то хоть одна из разностей ⁱ–ⁱ отлична от нуля. Это означает, что столбцы a₁,...,a_n линейно зависимы. В силу того, что если в матрице А столбцы (или строки) линейно зависимы, то det A=0, это противоречит тому, что det A0. Теорема до­казана.

N13  Свойства решений однородного линейного уравнения

   Ниже увидим, что знание частных решений однородного линейного уравнения значительно облегчает (а иногда позволяет до конца решить задачу полного интегрирования этого уравнения) построение общего решения. Это оказывается возможным благодаря тому, что частные решения однородного уравнения обладают следующими замечательными свойствами:

1. Если y₁ = y₁ (x) — частное решение однородного линейного уравнения L(y) = 0, то

            y = Cy₁,где C — произвольная постоянная, тоже является решением этого уравнения.

Таким образом, зная одно частное решение, можем (без квадратур!) получить целое (однопараметрическое) семейство решений.Это свойство иногда выражают так: решение однородного линейного уравнения определяется с точностью до постоянного множителя.

2. Если y₁ = y₁ (x) и y₂ = y₂ (x) — частные решения однородного уравнения L(y) = 0, то их сумма y = y₁ + y₂ тоже является решением этого уравнения.Наличие свойств 1 и 2 говорит о том, что множество решений однородного линейного уравнения является линейным пространством.

3. Если y₁, y₂, …, y_m — частные решения уравнения L(y) = 0, то

            y =  C_ky_k, где C₁, C₂, …, C_m — произвольные постоянные, тоже является решением этого уравнения.

N14

Однородные системы уравнений:

Однородная система АХ=0 всегда сов­местна, так как имеет тривиальное решение Х=0. Для существо­вания нетривиального решения однородной системы необходимо и достаточно, чтобы r=rang A<n (при т=п это условие означает, что det A=0). Пусть Q  Rⁿ множество всех решений однородной системы. Всякий базис в множестве Q состоит из n – r векторов e₁,...,e_n-r. Соответствующая ему в каноническом базисе система вектор-столбцов Е₁,..., Е_n–r наз. фундаментальной системой решений. Общее решение однородной системы имеет вид X= c₁E₁+...+c_n–rE_n–r,

где C₁,..., C_n–r – произвольные постоянные. Базисные решения Е₁,..., Е_n–r могут быть получены по правилу Крамера, если свободным неизвестным придавать пооче­редно значение 1, полагая остальные равными 0.

N15   Определение 15.7   Пусть    -- некоторое решение неоднородной системы линейных уравнений   ,    -- общее решение однородной системы   . Тогда выражение   называется общим решением неоднородной системы.         

Учитывая запись общего решения однородной системы через фундаментальную систему ее решений   , получаем для общего решения неоднородной системы формулу

И з двух последних предложений следует, что любое решение неоднородной системы может быть получено из общего решения при некоторых числовых значениях коэффициентов   .

        Предложение 15.5   Пусть    -- решение неоднородной системы   ,    -- любое решение однородной системы   . Тогда    -- решение неоднородной системы.           

Теорема 15.4   Система линейных уравнений   может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.

N16 Линейные операторы:

Линейным оператором в линейном пространстве L наз. всякое отображение A: LL пространства L в себя, обладающее свойствами A(x)=Ax и A(x+y)=Ax+Ay. Пусть A –линейный оператор в конечномерном пространстве L_n и В = (e₁,...,e_n) – некоторый фиксированный базис. Разложим векторы по базису В: Ae_k=a_1ke₁+...+a_nke, k=1,...,n. Тогда матрица

называется матрицей оператора A в базисе В. Матрицу оператора A будем иногда обозначать символом [A] или [A]_B, если существенно, о каком базисе идёт речь. Заданием матрицы оператор определяется однозначно, а именно: если y=Ax, то Y=AX, где X,Y – столбцы координат векторов x, y и A – матрица оператора A в базисе В. Пусть A и A' – матрицы оператора A в базисах B и B', а T=T_BВ' – матрица перехода от базиса B к базису B'. Тогда формула преобразования матрицы оператора при преобразовании базиса имеет вид A'=T^–1AT. Над линейными операторами, действующими в фиксированном пространстве L, вводятся следующие операции: (а) сложение операторов: (A+B)х=Ax+Bx; при этом [A+B]=А+В; (б) умножение операторов на числа: (A)x=(Ax); при этом [B]= B; (в) умножение операторов: (АВ)х=А(Вх); при этом [AВ]=АВ. Обратным к оператору А наз. оператор A^–1 такой, что AA^–1=A^–1A=E, где Е—единичный оператора реализующий тож­дественное отображение. Оператор A имеет обратный (и в этом слу­чае наз. невырожденным) в том и только в том случае, когда его матрица А невырождена (в любом базисе); при этом [A^–1]=A^–1.

N17

N18 Пусть 

^

A

:X_n → X_n — линейный оператор. Зададим в X_n два базиса: "старый" базис e = (e₁, e₂,  … , e_n) и "новый" базис f = (f₁, f₂,  … , f_n) .Матрицей перехода от базиса e к базису f называется матрица C = (c_ik)    (i,k = 1, … ,n) , столбцами которой являются координатные столбцы векторов f₁, f₂,  … ,f_n в базисе e , т.е.

f₁ = c₁₁ e₁ + c₂₁ e₂ + … + c_n1 e_n, f₂ = c₁₂ e₁ + c₂₂ e₂ + … + c_n2 e_n, … … … … … …  , f_n = c_1n e₁ + c_2n e₂ + … + c_nne_n,

или в матричной форме:

f = eC

(1)

где C — матрица перехода

C =	     	c11 c12 … c1n c21 c22 … c2n … … … … cn1 cn2 … cnn	     

Замечание. В силу линейной независимости базисных векторов матрица C — невырожденная ( det C ≠ 0 ). Следовательно, Cимеет обратную матрицу C ^{− 1} .Теорема 1. Преобразование координат вектора при переходе от "старого" базиса e к "новому" базису f определяется формулой:

X\f = C − 1X\e.