6. Алгоритм вычисления обратной матрицы:

1. Найти определитель исходной матрицы. Если = 0, то матрица А – вырожденная и обратная ей матрица не существует. Если , то матрица А – невырожденная и обратная матрица существует.

2. Найти матрицу , транспонированную к матрице А.

3. Найти алгебраические дополнения элементов транспонированной матрицы , , и составить из них присоединенную матрицу : , , .

4. Вычислить обратную матрицу по формуле: .

5. Проверить правильность вычисления обратной матрицы , исходя из ее определения: .

Вычисление обратной матрицы методом Гаусса:

1) к матрице А приписать справа единичную матрицу Е той же размерности;

2) путем преобразований методом Гаусса над строками расширенной матрицы (А | E) матрица А приводится к единичной матрице;

3) в результате вычислительного процесса на месте приписанной справа матрицы Е получится обратная матрица .

Схематично процесс нахождения обратной матрицы выглядит следующим образом: (А | E) (E | ).

Пример 3. Найти обратную матрицу методом Гаусса для .

Решение.

1.Составим расширенную матрицу .

2. Элементы первой строки умножим на (- 3) прибавим соответственно к элементам второй строки, получим . Затем элементы второй строки прибавим соответственно к элементам первой строки, получим . При выполнении следующего преобразования элементы второй строки умножим на (-1/2). В результате получим матрицу .

3. Итак, обратная матрица имеет вид .

Лекция 2

Системы линейных алгебраических уравнений. Методы их решения

Контрольные вопросы:

1. Определение системы линейных алгебраических уравнений.

2. Метод Крамера.

3. Метод Гаусса.

4. Метод обратной матрицы.

1. Система трех линейных уравнений с тремя неизвестными имеет вид

(4)

где - коэффициенты системы, - свободные члены . Определитель третьего порядка Δ, составленный из коэффициентов при неизвестных, называется определителем системы.

2. Если Δ ≠ 0, то единственное решение системы (4) выражается формулами Крамера:

, (5)

где - определители третьего порядка, получаемые из определителя системы Δ заменой первого, второго или третьего столбца соответственно столбцом свободных членов .

Систему (4) можно записать в матричной форме: , где

.

Тогда ее решение имеет вид

, (6)

если определитель матрицы А отличен от нуля.

3. Одним из наиболее универсальных методов решения систем линейных алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.

Процесс решения методом Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду (в частности, к треугольному) виду.

Для исходной системы т алгебраических уравнений п неизвестными

система в ступенчатом виде может быть представлена следующим образом:

где , , . Коэффициенты называются главными элементами системы.

На втором этапе (обратный ход) происходит последовательное нахождение неизвестных из этой ступенчатой системы.

Рассмотрим данный метод на примере решения системы (4). Будем считать, что элемент (иначе первым в системе запишем уравнение, в котором коэффициент при ). Используя элементарные преобразования системы (4), исключим неизвестное во всех уравнениях, кроме первого. Для этого умножим обе части первого уравнения на и прибавим соответственно ко второму уравнению системы. Затем умножим обе части первого уравнения на и прибавим соответственно к третьему уравнению системы. Получим эквивалентную систему

Здесь , ( ) – новые значения коэффициентов и правых частей, которые получаются после выполнения первого шага.

Аналогичным образом, считая главным элементом , исключим неизвестное из третьего уравнения системы. На этом шаге выполнение прямого хода заканчивается.

Второй этап (обратный ход) заключается в решении ступенчатой системы. В последнем уравнении выражаем и подставляем во второе уравнение найденное значение. Из второго уравнения находим и подставляем значения и в первое уравнение, из которого находим значение .

Замечание. На практике удобно работать не с системой (4), а с расширенной матрицей этой системы, выполняя элементарные преобразования над ее строками.

4. Метод обратной матрицы решения систем алгебраических уравнений заключается в нахождении обратной матрицы по одному из алгоритмов, представленных в п.4, и использовании формулы

для нахождения решения системы.

Замечание. Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т.е.

r < n, (7)

то система имеет бесконечное множество решений. Свободные n-r неизвестных выбираются произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.

Пример 4. С помощью формул Крамера найти решение системы линейных уравнений

(8)

Решение.

Вычислим определитель системы

.

Так как Δ ≠ 0, то решение системы может быть найдено по формулам Крамера (5). Для этого найдем :

.

Подставляя найденные значения определителей в формулы (5), получим искомое решение системы: .

Пример 5. Найти решение системы примера 4 с помощью обратной матрицы.

Решение.

Здесь

.

Так как определитель матрицы системы отличен от нуля: |A|=-26, то матрица А имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы . Транспонированная матрица имеет вид:

.

Согласно формуле (3), матрица , обратная к матрице _{А имеет вид}

.

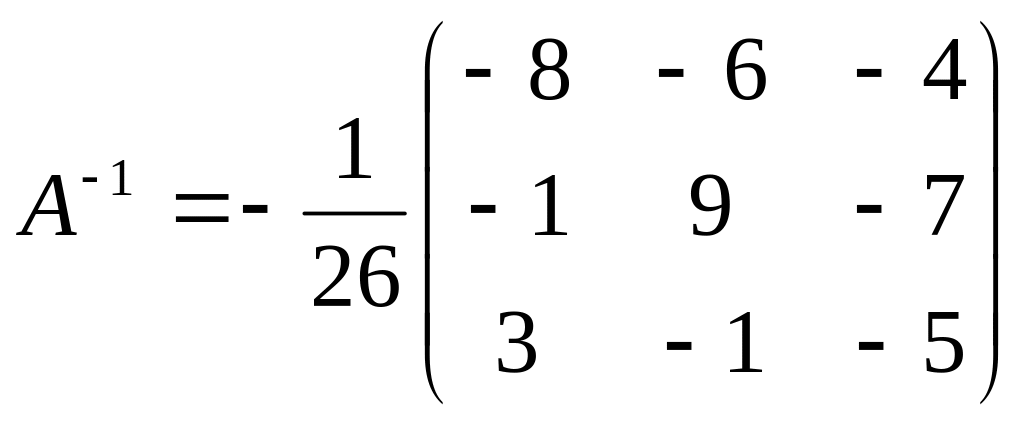Проверим правильность вычисления _{, исходя из определения обратной матрицы (2) и используя формулу (1):}

Матричное решение системы (8) в силу формулы (6) имеет вид

,

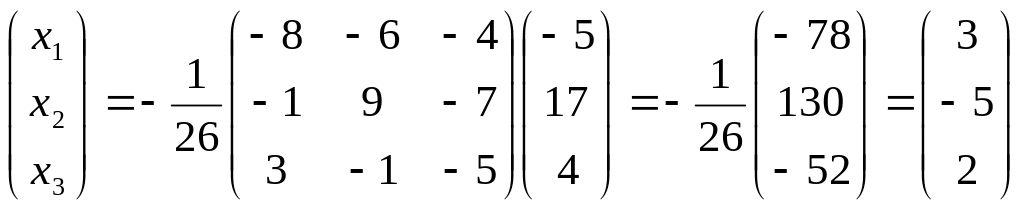откуда следует (из условия равенства двух матриц), что .

Пример 6. Решить систему линейных уравнений методом Гаусса:

Решение.

Здесь

.

Расширенная матрица системы имеет вид

.

Выполним прямой ход метода Гаусса.

Шаг 1. Для удобства вычислений поменяем местами первую и вторую строки:

.

Так как , то умножая первую строку на (-2) и на (-1) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную из всех строк, начиная со второй:

.

Шаг 2. Так как , то умножим вторую строку на (-3/5) и прибавим к третьей, таки образом исключим переменную из третьей строки:

.

Получили систему уравнений, соответствующую последней матрице:

откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения ; из второго уравнения найдем ; из первого уравнения .

Ответ: (3; -5; 2).

Пример 7. Решить систему линейных уравнений методом Гаусса:

Решение.

Здесь

.

Расширенная матрица системы имеет вид

.

Выполним прямой ход метода Гаусса. Для этого произведем элементарные преобразования над строчками расширенной матрицы системы:

̴ ̴ ̴

Полученная матрица соответствует системе

Выполним обратный ход метода Гаусса, найдем значения неизвестных: , , .

Ответ: (1; 1; 1).

Лекция 3