16.Прямая линия на плоскости.
Уравнение вида F(x,y)=0 есть уравнение линии на плоскости, если координаты всех точек, лежащих на этой линии удовлетворяют этому уравнению, а координаты точек, не лежащих на этой линии – не удовлетворяют.
Уравнение прямой, заданное уравнением первой степени общего вида Ax+By+C=0, называется уравнением прямой общего вида
Рассмотрим случаи:
В=0 → Ах+С=0 → прямая параллельная оси ОУ. В≠0 → Ву= -Ах-С → y=kx+b уравнение прямой с угловым коэффициентом, где k=-A/B, b=- C/B.
Угловым коэффициентом прямой называется тангенс угла, на который нужно повернуть против часовой стрелки ось Ох вокруг начала координат О, чтобы прямая стала параллельна этой оси.
Уравнение прямой с угловым коэффициентом
если в=0, →у=кх - уравнение пучка прямых, проходящих через начало координат.
если к=0, →у=в прямая параллельная оси Ох.
если к=0, в=0, →у=0 - уравнение оси Ох.
Уравнение прямой, проходящей через заданную точку (уравнение пучка прямых)
Любую прямую не параллельную оси Оу можно записать в виде у=кх+в.
Пусть прямая проходит через точку М(х0,у0). тогда справедливо у0=кх0+в. Вычтем у-у0=к(х-х0)
Ураснение прямой,проходящей через 2 заданные точки:
М1(х1,у1) →у-у1=к(х-х1) М2(х2,у2) →у-у2=к(х-х2) Поделим почленно
Уравнение прямой в отрезках на осях Ах+Ву+С=0 (2)
Если N(а,0) принадлежит прямой → Аа+С=0 (*) Если M(0,в) принадлежит прямой → Вв+С=0 (**)
Найдем из (*) и (**) А и В Подставив в (2) получим
Расстояние d от точки М0(х0,у0) до прямой, заданной уравнением общего вида Ax+By+C=0 определяется по формуле:
Пусть ( a, b, с ) и ( p, q, r ) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых:
aq – bp = br – cq = ar – cp = 0 ,
условие перпендикулярности прямых:
ap + bq + cr = 0 ,
угол 
между
прямыми:
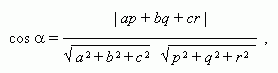
угол между прямой и плоскостью:
17.Эллипс:определение и вывод канонического уравнения.
Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина равная 2а.
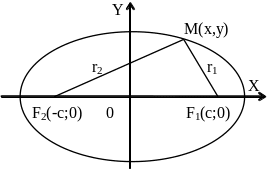
Эллипс
Обозначим F1F2=2c. Тогда координаты фокуса F1 будут (с;0), а координаты фокуса F2 будут (-с;0).
Определим r1 и r2 по формулам расстояния между двумя точками
На основании определения эллипса как геометрического места точек должно выполняться равенство:
r
1+r2=2a
вывод канонического уравнения эллипса
Преобразовав получим: каноническое уравнение эллипса
В уравнении эллипса содержатся только члены с четными степенями текущих координат. Отсюда следует важная геометрическая особенность: эллипс, определяемый уравнением (2) симметричен как относительно оси Ox, так и относительно оси Oy .
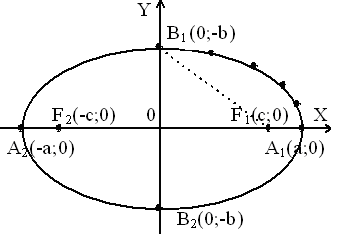эллипс
Э́ллипс (др.-греч. ἔλλειψις — недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух выделенных точек F1 и F2 (называемых фокусами) постоянна, то есть
|
F1M | + | F2M | = 2a.
Окружность является частным случаем эллипса. Эллипс можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Точка пересечения эллипса с осями называются его вершинами.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Расстояние
называется фокальным расстоянием.
Эксцентриситетом эллипса
называется отношение
фокусного расстояния
к длине большой оси эллипса;
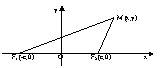Эллипсом
называется
геометрическое место всех
точек плоскости, сумма
расстояний от которых до
до фокусов есть величина
постоянная, большая, чем расстояние между фокусами.
Пусть М (х;у) – произвольная точка эллипса.
Т.к. MF1 + MF2 = 2a
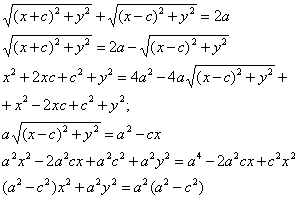
Т.к.
То
получаем
Или
