6. Производная и дифференциал

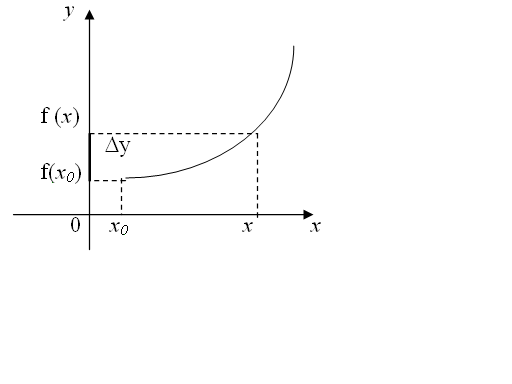
Пусть дана функция у = (х). Рассмотрим два значения ее аргумента: исходное х₀ и новое х.

Разность х = х - х₀ называется приращением аргумента х в точке х₀.

Разность у = у – у₀ =(х)- (х₀) называется приращением функции у = (х) в точке х₀ .

Определение производной.

Пусть функция у = (х) определена на промежутке Х. Возьмем точку хХ. Дадим значению х приращение х0, тогда функция получит приращение у = ( х+х ) - ( х ).

Производной функции у = (х) называется предел отношения приращения функции у к приращению аргумента х при стремлении х к нулю.

Производная функции у = (х) обозначается символом ( х).

Если функция в точке х₀ имеет конечную производную, то функция называется дифференцируемой в этой точке.

Производная функции у = (х) в точке х₀ является значением функции ( х) в точке х₀.

Функция дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.

Геометрический смысл производной.

Производная есть угловой коэффициент касательной (тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке х₀.

У равнение касательной к кривой y=f(x) имеет вид:

Правила дифференцирования

Производная постоянной равна нулю, т.е. С=0.

Производная аргумента равна 1, т.е. х=1

Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е. (u + v) = u + v.

Производная произведения двух дифференцируемых функций вычисляется по формуле: (u v) = u v + u v.

Следствие. Постоянный множитель можно выносить за знак производной: (Сu) = Cu.

Производная частного двух дифференцируемых функций может быть найдена по формуле:

7.Основные теоремы дифференциального исчисления.

Теорема Ферма. Если дифференцируемая на промежутке функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке x₀ этого промежутка, то производная функции в этой точке равна нулю, т.е. f′(x₀)=0.

Теорема Роля. Пусть функция y=f(x) удовлетворяет следующим условиям:

непрерывна на [a,b];

дифференцируема на [a,b];

на концах отрезка принимает равные значения, т.е. f(a)= f(b).

Тогда внутри отрезка существует по крайней мере одна такая точка

ε ( a,b), в которой производная равна нулю (f′(ε)=0).

Теорема Лагранжа. Пусть функция y=f(x) удовлетворяет следующим условиям:

непрерывна на [a,b];

дифференцируема на [a,b].

Тогда внутри отрезка существует по крайней мере одна такая точка

С( a,b), в которой производная равна частному от деления приращения функции к приращению аргумента на этом отрезке, т.е.

.

8.Функции нескольких переменных и их непрерывность.

Определение. Величина u называется функцией нескольких независимых переменных (x, y, z, …,t), если каждой совокупности значений этих переменных ставится в соответствие определенное значение величины u.

Если переменная является функцией от двух переменных х и у, то функциональную зависимость обозначают

z = f (x, y).

Символ f определяет здесь совокупность действий или правило для вычисления значения z по данной паре значений х и у.

Так, для функции z = x2 + 3xy

при х = 1 и у = 1 имеем z = 4,

при х = 2 и у = 3 имеем z = 22,

при х = 4 и у = 0 имеем z = 16 и т.д.

Аналогично называется величина u функцией от трех переменных x, y, z, если дано правило, как по данной тройке значений x, y и z вычислить соответствующее значение u:

u = F (x, y, z).

Здесь символ F определяет совокупность действий или правило для вычисления значения u, соответствующего данным значениям x, y и z.

Так, для функции u = xy + 2xz - 3yz

при х = 1, у = 1 и z = 1 имеем u = 0,

при х = 1, у = -2 и z = 3 имеем u = 22,

при х = 2, у = -1 и z = -2 имеем u = -16 и т.д.

Таким образом, если в силу некоторого закона каждой совокупности п чисел (x, y, z, …,t) из некоторого множества Е ставится в соответствие определенное значение переменной u, то и u называется функцией от п переменных x, y, z, …,t, определенной на множестве Е, и обозначается u = f (x, y, z, …,t).

Переменные x, y, z, …,t называются аргументами функции, множество Е - областью определения функции.

Частным значением функции называется значение функции в некоторой точке М0 (x0, y0, z0, …,t0) и обозначается f (М0) = f (x0, y0, z0, …,t0). Областью определения функции называется множество всех значений аргументов, которым соответствуют какие-либо действительные значения функции.

Функция двух переменных z = f (x, y) в пространстве представляется некоторой поверхностью. То есть, когда точка с координатами х, у пробегает всю область определения функции, расположенную в плоскости хОу, соответствующая пространственная точка, вообще говоря, описывает поверхность.

Функцию трех переменных u = F (x, y, z) рассматривают как функцию точки некоторого множества точек трехмерного пространства. Аналогично, функцию п переменных u = f (x, y, z, …,t) рассматривают как функцию точки некоторого п-мерного пространства.

Пусть имеется n переменных величин, и каждому набору их значений (x¹, х²... хⁿ) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z.

Тогда говорят, что задана функция нескольких переменных z = f (x¹, х² , ... хⁿ).

Например, формула z = π x₁² х₂ задает объем цилиндра z как функцию двух переменных: радиуса основания x₁ и высоты х₂ .

Линией уровня функции двух переменных z = f (x, у) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и тоже и равно С.