48.Числовые характеристикисистемы двух случайных величин.Зависимость между случайными величинами

Условным математическим ожиданием дискретной случайной величины Y при X=x (x- определенное возможное значение X) называют сумму произведений возможных значений Y на их условные вероятности:

• Д 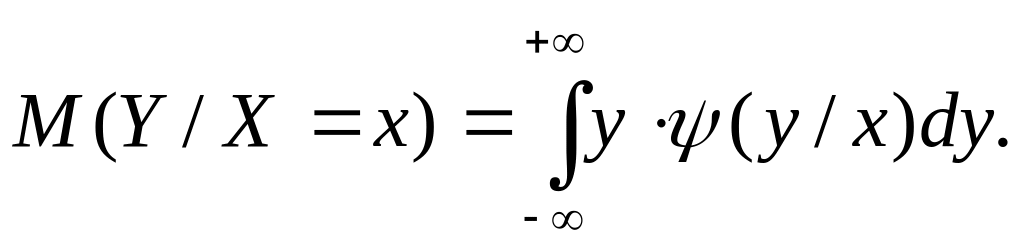ля непрерывных величин: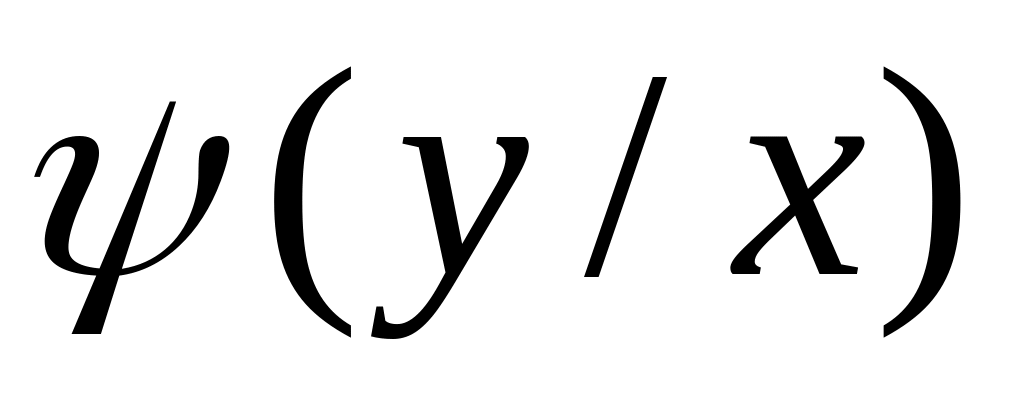

• 

• где - условная плотность случайной величины Y при X=x.

Зависимые и независимые случайные величины

• Теорема. Для того, чтобы случайные величины X и Y были независимыми необходимо и достаточно, чтобы функция распределения системы (Х, У) была равна произведению функций распределения составляющих: F(x,y)= F₁(x)F₂(y)

• Ковариацией (или корреляционным моментом) называется математическое ожидание произведения отклонения этих величин от своих математических ожиданий:

49. Неравенство Чебышева.

Теорема. Если Х₁, Х₂, …, Х_n- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства

будет сколь угодно близка к единице, если число случайных величин достаточно велико.

 

            Т.е. можно записать:

 

            Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:

            Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.

            Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.

            Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.

            Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.

50. Закон больших чисел и его следствие.

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Слабый закон больших чисел

Пусть есть бесконечная последовательность одинаково распределённых и некоррелированных случайных величин , определённых на одном вероятностном пространстве . То есть их ковариация . Пусть . Обозначим S_n выборочное среднее первых n членов:

.

Тогда .