2.3. Расчет объемов аспирации конвейерных перегрузок

Наиболее распространенный случай, когда аспирационное укрытие связано с окружающей атмосферой тремя путями:

1. Посредством отверстий (неплотности, рабочие проемы), через которые под действием разряжения воздух поступает в укрытие;

2. Посредством желоба, по которому в укрытие поступает воздух (эжектируемый материалом, или нагнетаемый ротором дробилки);

3. Посредством аспирационной воронки, через которую воздух отсасывается через укрытия. Воздушный баланс для этого случая имеет вид:

Q_a

Q_ж

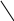
Qн

Основное уравнение аспирации:

Qа = Qж + Qн. (2.4)

Расход воздуха, поступающего через неплотности

Количество воздуха, поступающего в укрытие через неплотности определяется разностью давлений и гидравлическим сопротивлением каналов, по которым перетекает воздух.

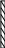
Р₂ Uн Р_атм

(2.5)

где

Ратм – абсолютное давление вне укрытия (Па);

Р₂ – абсолютное давление в укрытии (Па);

Uн – скорость воздуха в неплотности (м/с);

ρ – плотность воздуха (кг/м³).

Разряжение в укрытии:

Ратм –Р₂ = Ру . (2.6)

С учетом (2.6) получим:

, (2.7)

Qн= Uн*Sн= Sн (2.8)

где

Sн- площадь неплотностей (м²).

Чаще всего ζн = 2,4.

. (2.9)

Таким образом, количество воздуха поступающего в укрытие через неплотности определяется величиной разряжения Ру, поддерживаемого в укрытии за счет отсоса воздуха в укрытии вентилятором, и общей площадью неплотности Sн.

Величина оптимального разряжения Ру устанавливается из условий полного исключения выбивания пыли наружу (санитарно- гигиенические требования).

Активируемый уголь	Ру, Па	Sн, м2 не более
1. Природный барабан ленточного укрытия	5	1,2 Вк
2. Узел загрузочного конвейера а) одинарное укрытие б) укрытие с двойными стенками	10 6	0,02П 0,02П
3. Дисковый (тарельчатый) питатель	6	0,1Дп
4. Барабанный смеситель	12	0,03Дб
5. Конусная дробилка	4	0,05Дк
6.Грохоты (укрытия кабинного типа)	5	0,04Fгр

где:

Вк – ширина ленты конвейера, м;

П – периметр укрытия в плане, м;

Дп – диаметр диска питателя, м;

Дб – диаметр барабана смесителя, м;

Дк – диаметр конуса дробилки, м;

Fгр – площадь решотки грохота, м² .

Общий принцип определения расхода воздуха в желобе:

Найдем количество воздуха, поступающее в укрытие по желобу Qж. Запишем уравнение динамики воздуха в желобе для случая, когда перегружается нагретый материал, т.е. когда в желобе действует помимо эжекционного давления (Рэ, Па) и тепловое давление ( Рт, Па).

Q_a1

Q_н1 Р₁ Р_атм

Р_Т Q_а2

Р_э

Uж

Р₂ Q_н2

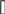
Уравнение динамики:

Р₁ –Р₂+Рэ-Рт= (2.10)

Или, заменяя абсолютное давление в укрытии на величину разряжения получим:

(2.11)

Уравнение гидравлики:

,

(2.12)

Расход воздуха через желоб составляет:

. (2.13)

Эжекционное давление – это сумма аэродинамических сил всех частиц, падающих в желобе, деленная на площадь поперечного сечения желоба.

Р₁ О Y

V_н

ℓ dх

S

Р₂ V_k

где х

R –аэродинамическая сила одной частицы;

n- концентрация частиц в единице объема;

Sdx –объем;

nSdx –количество частиц в элементарном объеме.

(2.14)

Т.к. концентрация частиц ( шт/м³ ),

где

β- объемная концентрация падающих частиц (м³/м³ ),т.е это доля объема занятого частицами.

(2.15)

(2.16)

где

R- аэродинамическая сила одной падающей частицы ( в желобе);

ψ – коэффициент лобного сопротивления частиц;

Sм – площадь миделевого сечения, чаще всего принимается равной:

, (2.17)

где

dэ – эквивалентный диаметр частиц (диаметр шара, равный по массе нашей частице);

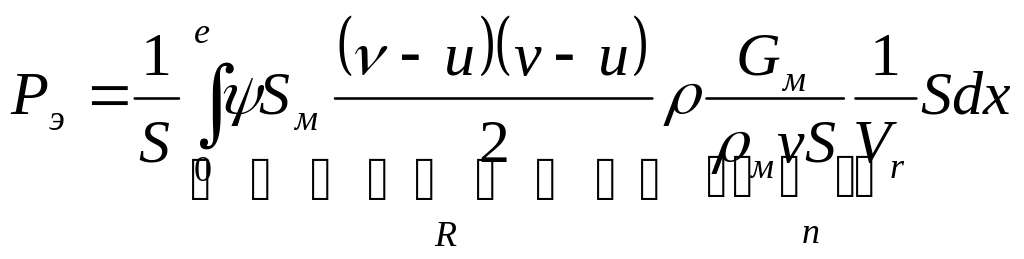, (2.18)

где

u – скорость воздуха в желобе, м/с;

ρ- плотность воздуха в желобе.

Рассмотрим случай равноускоренного падения частиц (падения тяжелых частиц):

,

,

,

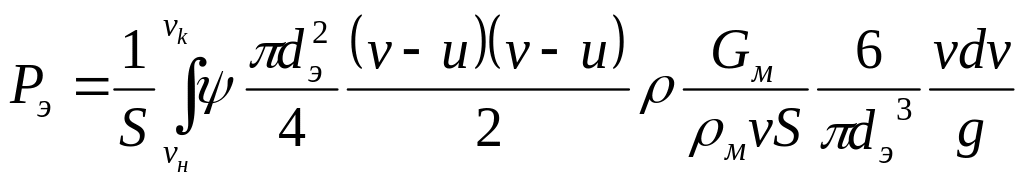. (2.19)

Интегрируя это при u=const, получим:

, (2.20)

где

Ψ – коэффициент лобового сопротивления частиц.

Закон Стокса :

, (2.21)

Для частиц шарообразной формы :Ψ₀ =0,5;

Для округлых частиц ( в 3): Ψ₀ = 1,0;

Для острозернистых частиц: Ψ₀ = 1,8.

Для частиц в потоке коэффициента лобового сопротивления Ψ зависит от объемной концентрации падающих частиц – чем больше концентрация, тем больше проявляется взаимное влияние частиц на аэродинамическое обтекание. Поэтому для определения Ψ используется следующая формула:

, (2.22)

где

Ψ₀ – коэффициент любого сопротивления одиночной частицы в области автомодельности;

β – объемная концентрация;

d_э – диаметр шара, эквивалентного частице по объему [мм]. , (2.23)

, (2.24)

где

, (2.25)

Тепловой напор:

, (2.26)

где

Н- высота падения материала, мм;

ρ ₀ – плотность воздуха в помещении [кг/м³] (при t=20⁰ C ρ₀=1,213кг/м³);

ρ – плотность воздуха в желобе, которая будет ниже плотности ρ ₀ при перегрузках нагретого материала за счет теплообмена между частицами и воздухом.

, (2.27)

где

t- температура воздуха в желобе.

При расчетах эжекции воздуха в желобах при перегрузках нагретого материала t определяется по формуле:

, (2.28)

где

t_м – температура перегрузочного материала, ⁰С;

t₀- температура воздуха внутри помещения, ⁰С;

К_t- поправочный коэффициент;

К_t = 0,2……1 – зависит от (t_м –t₀) чем меньше эта разность, тем К_t ближе к 1.

Критериальное уравнение для определения расхода воздуха в желобе:

Итак, скорость воздуха, поступающего по желобу определяется уравнением гидравлики.

, (2.29)

где

Р₁- разряжение в верхнем укрытии (оптимальное), Па;

Р₂- оптимальное разряжение в нижнем укрытии, Па;

Р_э – эжекционное давление, Па;

Р_Т – тепловое давление, Па;

∑ζ – сумма к.м.с. желоба;

U –скорость воздуха в желобе;

ρ- плотность воздуха в желобе.

Или с учетом полученного выражения для Р_э ( для случая вертикального желоба при равноускоренном падении частиц):

.(2.30)

Разделим обе части этого уравнения на и введем понятие коэффициент эжекции φ:

, (2.31)

- критериальное уравнение

где Е_u – критерий Эйлера:

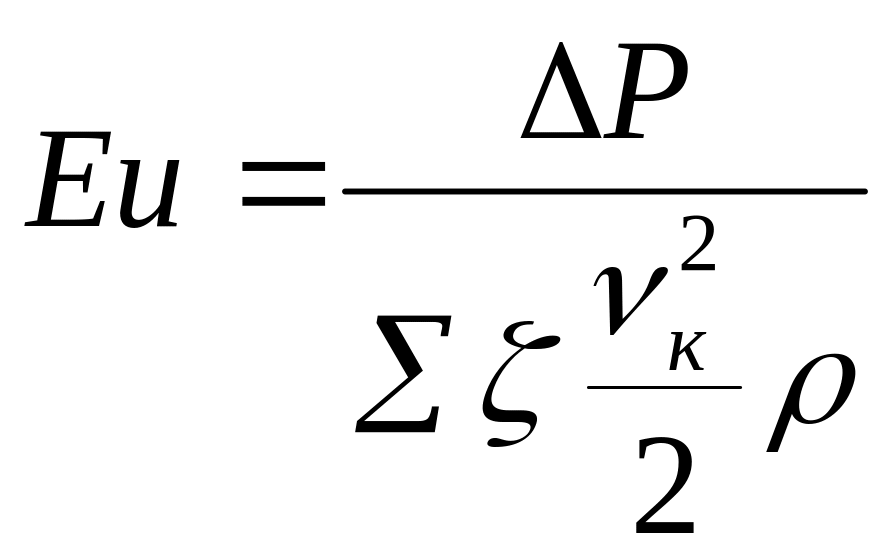, . (2.32)

Е_u характеризует зависимость коэффициентов эжекции (φ) от разряжений в укрытии и теплового напора. , (2.33)

где

В_u - число Бутакова – Нейкова, который характеризует зависимость коэффициента эжекции от количества частиц и их аэродинамического сопротивления.

Таким образом, зная коэффициент φ, найдем расход воздуха в желобе:

, (2.34)

φ может быть с "-" – это противоток (воздух вверх по желобу).