20.Модель международной торговли (модель обмена). Условие бездефицитности.

Модель международной торговли (коротко: модель обмена)служит для ответа на следующий вопрос: какими должны быть соотношения между государственными бюджетами стран, торгующие между собой, чтобы торговля была взаимовыгодной, т.е. не было значительного дефицита торгового баланса для каждой из стран участниц. Проблема достаточно важна, так как дефицит в торговле между странами порождает такие явления, как лицензии, квоты, таможенные пошлины и даже торговые войны.

Д ля простоты изложения рассмотрим три страны- участницы торговли с государственными бюджетами x₁, x₂, x₃. Будем считать, что весь госбюджет каждой страны тратится на закупку товаров либо внутри страны, либо на импорт из других стран. Введём структурную матрицу торговли, каждый элемент которой a_ij определяет долю бюджета j-й страны, которую она тратит на закупку товаров у i-й страны:

Заметим, что по определению структурной матрицы, торговли суммы элементов матрицы A по столбцам равны 1, поскольку предполагается, что все бюджеты полностью расходуются (сумма всех долей должна быть равна 1).

П осле проведения итогов торгов за год страна под номером i получит выручку:

(2.1)

Для того чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны:

для всех i. (2.2)

Перепишем в матричном виде условие бездефицитности торговли:

,

где X- бюджетный вектор, P – вектор выручки:

, P=

Теорема. Условием бездефицитности торговли является равенство:

, i = 1, 2, 3.

Доказательство. Предположим, что для некоторого i, например, для i=1. Запишем условие (2.2) для всех i:

Сложив все эти неравенства, получим:

Поскольку все суммы в скобках в левой части неравенства равны1, то получим противоречивое неравенство

Следовательно, наше предположение о том, что , i =1 неверно.

Доказательство завершено.

В матричной форме утверждение, содержащееся в теореме, выглядит следующим образом:

( 2.3)

Таким образом, моделирование бездефицитного обмена свелось к так называемой проблеме собственных значений и собственных векторов структурной матрицы торговли, причём, бюджеты бездефицитно торгующих страны являются компонентами собственного вектора матрицы A, принадлежащие её собственному значению, равному 1.

21. Модель международной торговли. Теорема о цепочке

Данная модель служит для ответа на вопрос: какими должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была выгодной, т.е. не было дефицита торгового баланса для любой из стран. Данная проблема является важной, т.к. дефицит в торговле порождает такие явления как лицензии, квоты, таможенные пошлины и торговые войны.

Определение: Говорят, что страны i и j связаны цепочкой импорта от i к j, если существует цепочка стран с началом в стране i и концом в стране j, в которой каждая

последующая страна импортирует товары из предыдущей страны.

Теорема: (О цепочке). Если в модели международной торговли структурная матрица A такова, что любые две страны i и j можно связать цепочкой импорта i → j, то уравнение AX’= X’ имеет положительное решение единственное X̅ > 0, с точность до множителя на число.

Доказательство: Пусть n - число рассматриваемых стран. Тогда любые две страны можно связать цепочкой импорта произвольной длины. Причем можно связать и цепочкой в которой не более n стран (путем удаления замкнутых петель). Если страны i и j можно соединить цепочкой импорта (от i к j) содержащей k стран, то элемент i-ой строки и j-го столбца матрицы 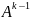больше нуля, т.е. >0. Данное заключение следует из того, что этот

элемент является суммой неотрицательных произведений вида · ·…· по всем цепочкам → →…→ от i к j ( = i, = j). Для рассмотренной выше цепочки импорта (1 → 4 → 3 → 2 → 1) элемент = + + + + + + + + + + + + + + +

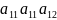Все эти слагаемые больше нуля, т.к. являются произведениями элементов неотрицательной

матрицы A. Кроме того, по крайней мере одно слагаемое, благодаря существованию цепочки, не равно нулю.

Значит >0. В общем случае, если i ≠ j и существует цепочка импорта, то для матрицы A хотя бы одно из чисел , , … , больше нуля, а значит и сумма ( + …+ ) > 0.

Добавим к матрице единичную матрицу, получим B = E + A + +…+ > 0.

Пусть x̅ - собственный вектор матрицы A, соответствующий собственному значению λ. Тогда Bx̅ = (E + A + +…+ ) x̅ = x̅+λx̅+ x̅+…+ x̅ = =(1+λ+ +…+ ) x̅

т.е. вектор x̅ является собственным вектором матрицы B, соответствующий собственному значению (1+λ+ +…+ ). И дальнейшее доказательство теоремы следует из теоремы Фрабениуса-Перрона....