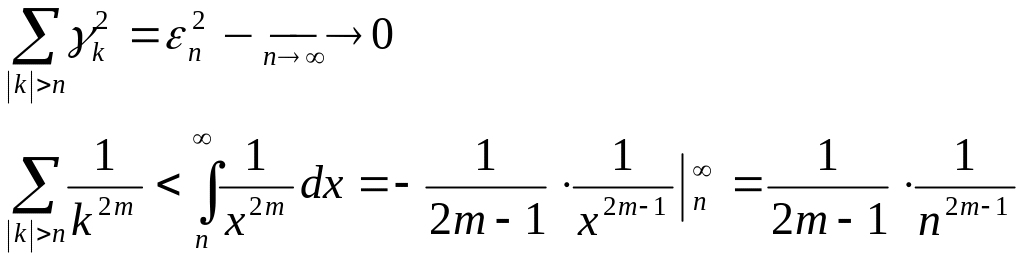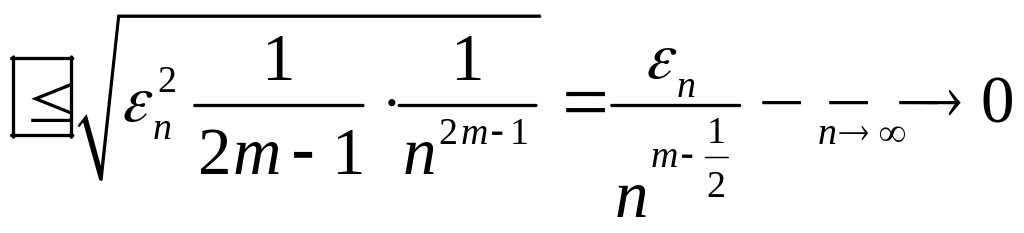- •11. Ряд Лорана аналіт.Функції, його єдинственність для анал.Функц.
- •12. Теорема Лорана про розвинення анал.Функції в ряд Лорана
- •13. Ізольовані особливі точки. Класифікація.
- •14. Теорема про правильну точку аналітичної функції.
- •15. Полюси. Необхідна і достатня умова полюса к-го порядку.
- •16. Зв’язок характеру особливої ізольованої точки з виглядом розкладу в ряд Лорана в околі цієї точки
- •17. Характер нескінченно віддаленої особливої точки
- •18. Лишки. Їх зв’язок з інтегралом по замкненій кривій
- •19. Обчислення лишків
- •20. Лишки в нескінченно віддаленій точці
- •21. Застосування лишків для обчислення визначених інтегралів
- •22. Застосування лишків до невласних інтегралів
- •23. Застосування лишків до невласних інтегралів
- •24. Тригонометричні ряди Фур’є
- •25. Абстрактні ряди Фур’є
- •26. Нерівність Коші-Буняковського та теорема Піфагора.
- •27. Основні властивості коефіцієнтів Фур’є. Нерівність Бесселя
- •Нерівність Бесселя
- •28. Поточкова збіжність тригонометричних рядів Фур'є
- •29. Лема Рімана та наслідок з неї.
- •30. Достатня умова збіжності ряду Фур’є в точці.
- •31. Теорема Фейєра та наслідки з неї.
- •32. Зв’язок швидкості спадання коефіцієнтів ряду Фур’є з гладкістю функції
- •33. Теорема про повноту тригонометричної системи
- •34. Перетворення Фур’є, існування, властивості.
- •35. Достатні умови представлення функції в інтеграл Фур’є
- •36. Перетворення Лапласа. Аналітичність перетворення Лапласа.
- •37. Властивоcті перетворень Лапласа
- •38. Диференціювання та інтегрування оригінала та зображення
- •39. Згортка функції. Зображення згортки.
- •40. Обернене перетворення Лапласа. Формула Рімана-Меліна
- •41. Лема Жордана. Формула обернення.
31. Теорема Фейєра та наслідки з неї.
Розглянемо послідовність
функцій![]() ,
що є середнім арифметичним часткових
сум ряду Фур’є:
,
що є середнім арифметичним часткових
сум ряду Фур’є:
![]() .
Тоді
.
Тоді
![]()

ядро Фейєра:
 - середнє арифметичне ядер Діріхле.
- середнє арифметичне ядер Діріхле.
Властивості
1)

2)![]()
3)![]()
Якщо позначити через
![]()
Тоді справедливо
1)![]()
2)![]() .
.
Доведення
1) Очевидно
2) Використаємо лему Рімана. Для ядра Фейєра

Теорема Фейєра
Нехай
![]() -
-
періодична абсолютно інтегрована на
інтервалі
-
-
періодична абсолютно інтегрована на
інтервалі
![]() функція.
функція.
Тоді:
1) Якщо на деякій
множині Е
- рівномірно- неперервна, то
![]() на Е
на Е
2) Якщо - неперервна то на R при
![]()
3)Якщо
в точці х
то
![]() при
.
при
.
Доведення
Твердження 2) і 3) - наслідки 1), тому що функція, неперервна на будь-якому вілрізку, рівномірно неперервна на ньому. Тому досить довести твердження 1)
1) - абсолютно інтегрована , рівномірно неперервна на Е вона обмежена
![]()
- рівноміоно неперервна
![]()
Позначимо
![]() - окіл точки.
- окіл точки.
Тоді можна записати послідовність

Доведено.
Наслідок 1
(теорема Вейєрштраса про апроксимацію тригонометричними поліномами)
Якщо
![]() неперервна на цьому відрізку і
неперервна на цьому відрізку і
![]() ,
то ця функція може бути як завгодно
точно рівномірно на
,
то ця функція може бути як завгодно
точно рівномірно на
![]() апроксимована тригонометричними
поліномами.
апроксимована тригонометричними
поліномами.
Наслідок 2
Якщо функція неперервна в точці х , то її ряд Фур’є або розходиться або збігається в цій точці до .
Доведення
Якщо розбігається – доводити нічого.
Якщо збігається, існує
![]() ,
то послідовність середніх значень цих
величин
,
то послідовність середніх значень цих
величин
![]() теж збігається до тієї ж самої величини.
Але з т.неперервності відомо, що
послідовність сум Фейєра збігається
до значення функції.
теж збігається до тієї ж самої величини.
Але з т.неперервності відомо, що
послідовність сум Фейєра збігається
до значення функції.
З теореми Фейєра
![]() в точці неперервності
в точці неперервності
![]() ,
що і треба було довести.
,
що і треба було довести.
32. Зв’язок швидкості спадання коефіцієнтів ряду Фур’є з гладкістю функції
Степінь гладкості функції в точці – кількість похідних, які функція має в цій точці.
Лема( Диференціювання ряду Фур’є)
Якщо неперервна
функція
![]() ,
можливо комплекснозначна. Має однакові
значення на кінцях інтервалу, отже, її
можна зробити періодичною.
Кусково-неперервно-диференційована
для неї виконано умови теореми Діні .
Ряд Фур’є її похідної
,
можливо комплекснозначна. Має однакові
значення на кінцях інтервалу, отже, її
можна зробити періодичною.
Кусково-неперервно-диференційована
для неї виконано умови теореми Діні .
Ряд Фур’є її похідної
![]()
![]()
![]() можна отримати
формальним диференціюванням ряду Фур’є
самої функції
,
якій відповідає ряд Фур’є
можна отримати
формальним диференціюванням ряду Фур’є
самої функції
,
якій відповідає ряд Фур’є
![]() .
.
![]() .
(*)
.
(*)
Доведення
З теореми , що для всіх функцій ряд Фур’є існує.
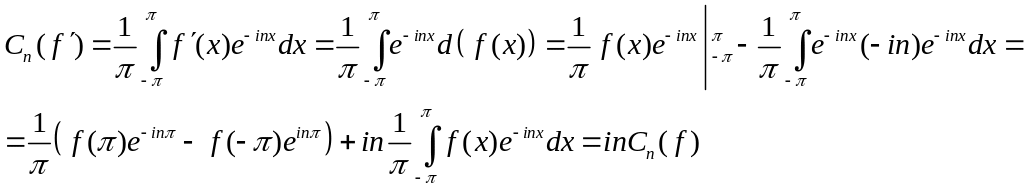
Твердження
Нехай
![]()
![]()
Якщо
![]() має кусково-неперервну
має кусково-неперервну
![]() - ту похідну (похідні до порядку
просто неперервні).
- ту похідну (похідні до порядку
просто неперервні).
То
![]()
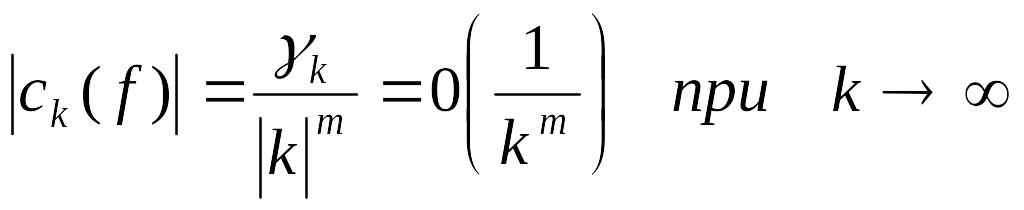 ,
,
причому
![]() .
.
Доведення
Застосовуючи (*) m
разів, отримуємо
![]()
Позначивши
![]() ,
отримуємо
,
отримуємо
![]() .
.
З нерівності Бесселя
отримуємо
 .
.
Зауваження
Враховуючи, що в
дійсному вигляді зв”язок між
![]() відомий,
відомий,
![]() ,
,
![]()
![]() такі, що при
такі, що при
![]()
![]() .
.
Теорема
Якщо f
– неперервна , 2
-
періодична функція , і вона має на
інтервалі
![]() кусково- неперервну похідну
кусково- неперервну похідну
![]() порядку
порядку
![]() ,
то її ряд Фур’є збігається до f
абсолютно і рівномірно на всьому періоді,
причому відхилення часткових сум
від f
можна оцінити нерівністю
,
то її ряд Фур’є збігається до f
абсолютно і рівномірно на всьому періоді,
причому відхилення часткових сум
від f
можна оцінити нерівністю
 .
.
Доведення
![]() .
f
.
f![]() задовольняє умовам твердження
задовольняє умовам твердження![]() .
.
Тоді
 - збігається, оскільки за нерівністю
Коші-Буняковського
- збігається, оскільки за нерівністю
Коші-Буняковського
![]()
![]() - збігається абсолютно і рівномірно на
за критерієм Вейєрштраса.
- збігається абсолютно і рівномірно на
за критерієм Вейєрштраса.
![]() - мажоранта для
- мажоранта для
![]() .
Причому ряд
.
Причому ряд
![]() збігається до функції
, оскільки в усіх точках інтервалу
виконані умови Діні (кусково-неперервна
похідна ).
збігається до функції
, оскільки в усіх точках інтервалу
виконані умови Діні (кусково-неперервна
похідна ).
Оцінка похибки