21. Застосування лишків для обчислення визначених інтегралів
1) Для обчислення
інтегралів
, де
- раціональна ція двох дійсних змінних,
неперервна при
.
За формулою Ейлера
Позначимо
.
Коли
пробігає від
до
,
описує коло проти годинникової стрілки.
Таким чином,
(
- раціональний вираз відносно
,
має скінченне число особливих точок
всередині кола
).
22. Застосування лишків до невласних інтегралів
Лема Жордана
:
Нехай
- аналітична в верхній півплощині (
)
за винятком скінченного числа особливих
точок
:
Доведення
Нехай
.
Тоді при
аналітична на
і
Наслідок 1
Якщо
така, що задовольняє умовам леми, то
Нехай
При
отримуємо
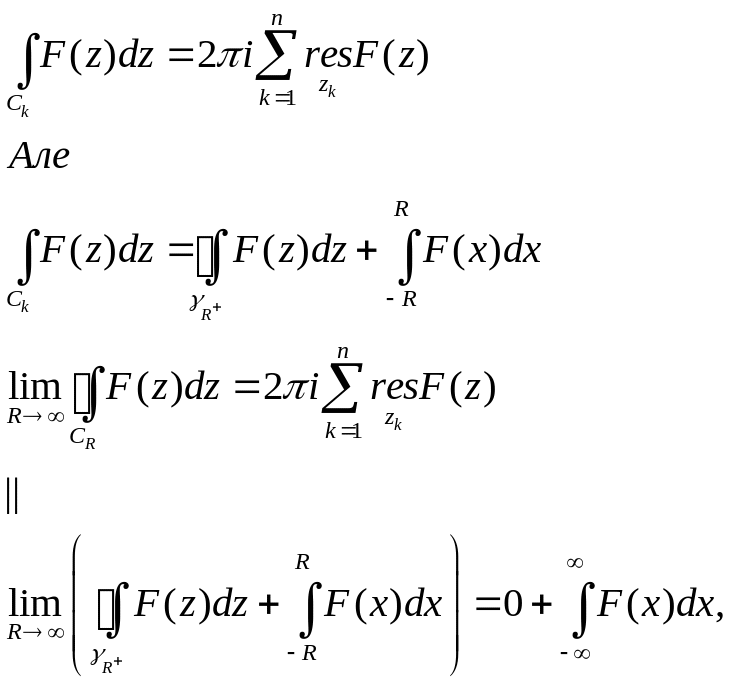
що й треба було довести.
Наслідок 2
Розглянемо
і
не має дійсних коренів. Тоді
аналітична у верхній півплощині за
винятком, можливо, скінченного числа
полюсів
(в правильних точках
,
тому вони нас не цікавлять).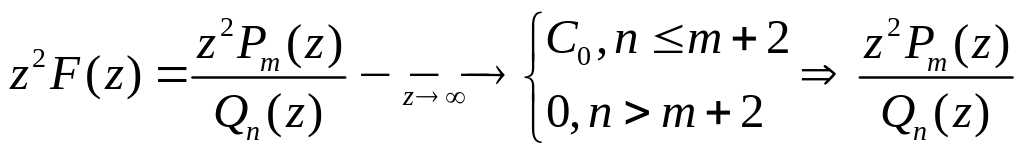
- обмежена при
-
виконуються умови леми Жордана і
наслідка.
Наслідок 3
- всі полюси верхньої півплощини.
3) Послаблення вимог до підінтегральної функції
Нехай
аналітична в півплощині
за винятком, можливо, скінченного числа
особливих точок
.
Нехай
(
).
Тоді для
функція
буде неперервною на
.
Тоді якщо
Доведення
Спочатку покажемо,
що в цому випадку за цих умов
(лема Жордана 2 – буде розглянута в
наступній лекції).
Значить, існує
Теорема
Якщо
,
то
23. Застосування лишків до невласних інтегралів
Нехай аналітична в півплощині за винятком, можливо, скінченного числа особливих точок . Нехай ( ). Тоді для функція буде неперервною на .
Тоді якщо
Доведення Спочатку покажемо, що в цому випадку за цих умов (лема Жордана 2 – буде розглянута в наступній лекції).
Значить, існує
Теорема Якщо , то
Доведення
Розглянемо замкнену
криву
.
Тоді
.
(*)
Лема Жордана 2
В умовах теореми
.
Доведення
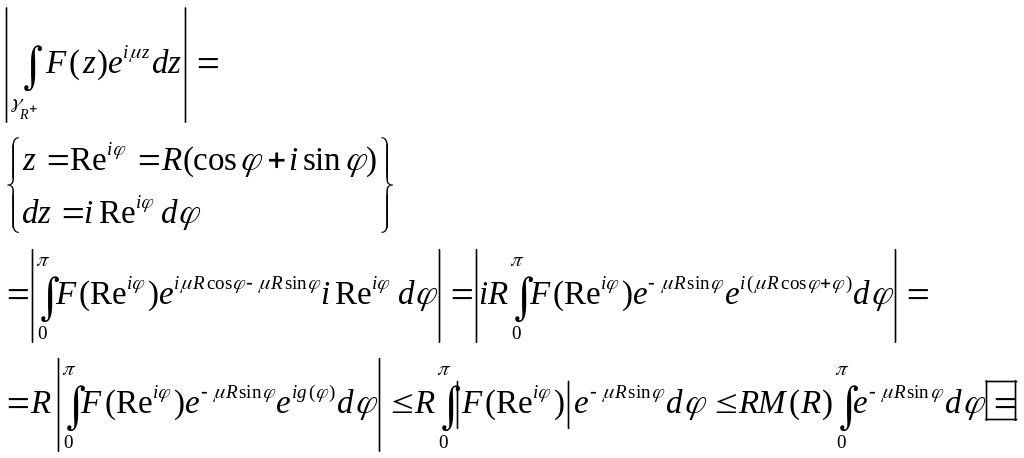
Зауваження
оскільки
, а
Використаємо оцінку
.
Оскільки
;
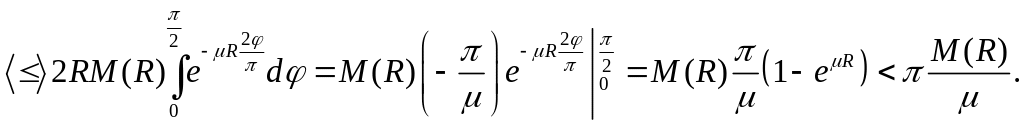
Отримали
Але
,
Лему Жордана доведено.
Продовження доведення теореми(*) Таким чином, отримали
,
і т.д.
,
що й треба було довести.
1) Якщо
парна
Висновок: для парної
2) Якщо
непарна
Висновок: для непарної
24. Тригонометричні ряди Фур’є
Тригонометричний
ряд
(1)
Його часткові суми:
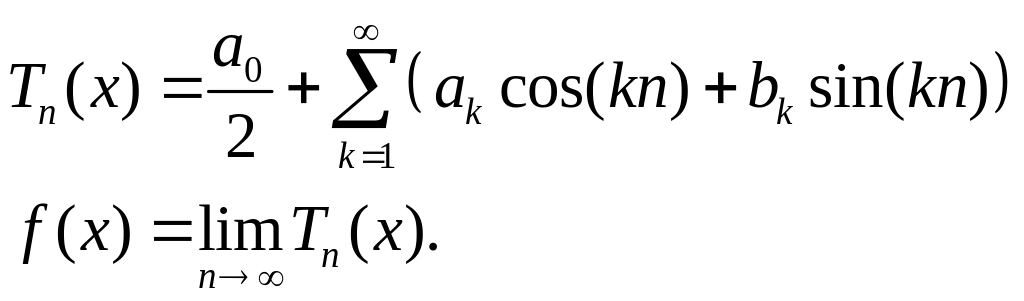
Якщо ряд (1) збігається
до
,
то
- періодична функція з періодом
.
Зв’язок між коефіцієнтами та
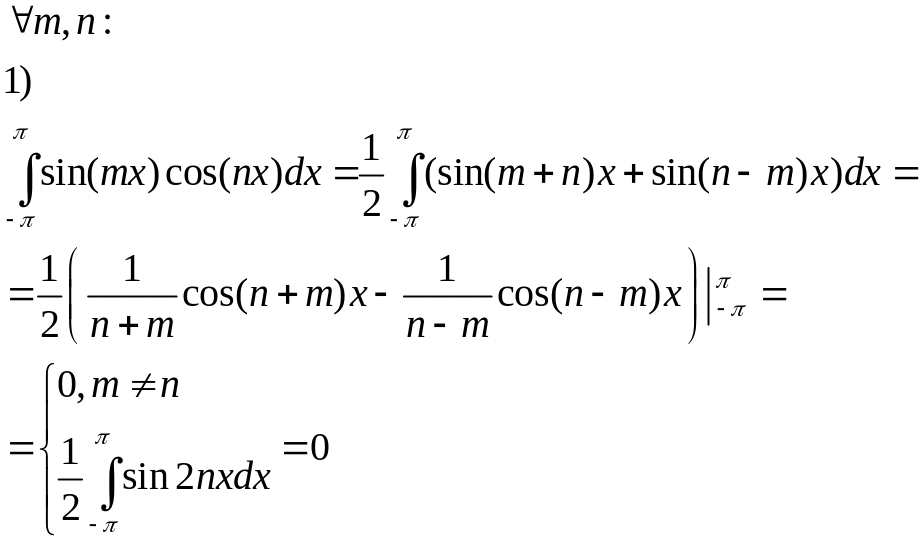
оскільки
При
.
Теорема
Якщо
(1) збігаєтья рівномірно на періоді
,
рівномірно збігається
-
неперервна функція. Інтегруємо почленно:
Якщо інтеграли
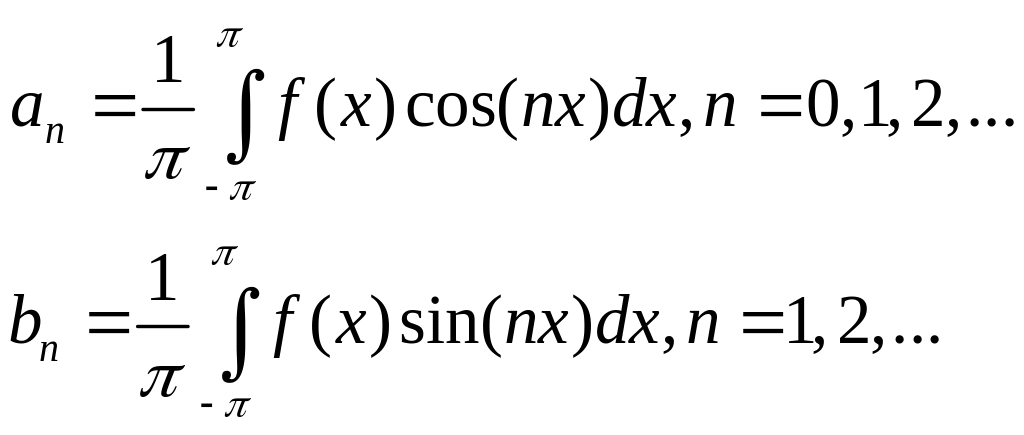мають
сенс, то відповідний тригонометричний
ряд
називається тригонометричним
рядом Фур’є
.
1) Якщо
- парна функція, то
- парна,
- непарна.
Тоді
Ряд Фур’є має вигляд
(розклад лише за косинусами).
2) Якщо - непарна функція, то - непарна, - парна.
Тоді
Ряд
Фур’є має вигляд
(розклад лише за синусами).