16. Зв’язок характеру особливої ізольованої точки з виглядом розкладу в ряд Лорана в околі цієї точки

1) Якщо головної частини немає, - правильна точка

2) В головній частині – скінченне число доданків

- полюс -го порядку.

Навпаки, якщо - полюс -го порядку,

- аналітична в деякому околі

Якщо в головній частині – нескінченнне число доданків, то це суттєво особлива точка.

- суттєво особлива точка.

17. Характер нескінченно віддаленої особливої точки

Нехай - аналітична в області (окіл нескінченності). Тоді Заміна . Відповідна послідовність .

За визначенням покладемо для функції: якщо точка - проста, полюс -го порядку (або суттєво особлива точка), тоді для точка буде простою, полюсом -го порядку або суттєво особливою точкою.

Стосовно ряду Лорана

1) Проста точка для (в околі 0).

Відповідно

2) Полюс - го порядку .

3) Суттєво особлива точка

- нескінченне число від’ємних елементів. - нескінченне число додатніх елементів. Висновок: в околі нескінченності роль головної частини грають члени з додатніми степенями.

18. Лишки. Їх зв’язок з інтегралом по замкненій кривій

Означення

Нехай - замкнена спрямляєма крива, і - функція, аналітична на ній і всередині її, крім, можливо, деякої точки всередині кривої. Тоді називається лишком в точці і позначається .

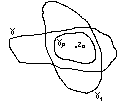
Означення несуперечливе, оскільки - ен на границі, всередині обох кривих , яка повністю всередині обох кривих ( ).

.

Основна теорема про лишки

Теорема

Нехай - аналітична на - границі області , і в самій області, крім, можливо, скінченного числа точок Тоді

Доведення

Оточимо кожну з цих точок ( ) замкненими кривими так, щоб вони не мали спільних точок.

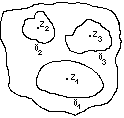
Розглядаємо . За теоремою Коші для багатозв’язних областей

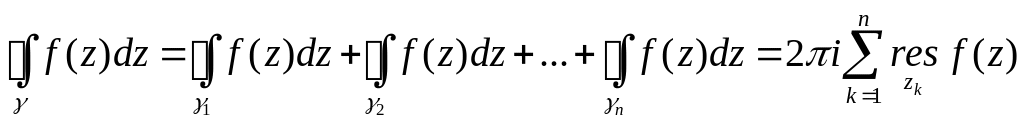
19. Обчислення лишків

Твердження 1

Якщо - ізольована особлива точка - аналітична. За теоремою Лорана

При отримуємо що й треба було довести.

Отже, якщо - проста точка функції , то

Лишки в полюсі

Нехай в точці має полюс - го порядку.

- ряд збігається рівномірно в , - степеневий ряд - аналітична.

- неперервна в (ця функція і всі її похідні аналітичні в даній точці, неперервні). . Таким чином, ми отримали

Наслідок

Якщо точка - простий полюс для , то

Окремий випадок

Нехай

Тоді при точка - правильна для , і Якщо , тоді - простий полюс для , і

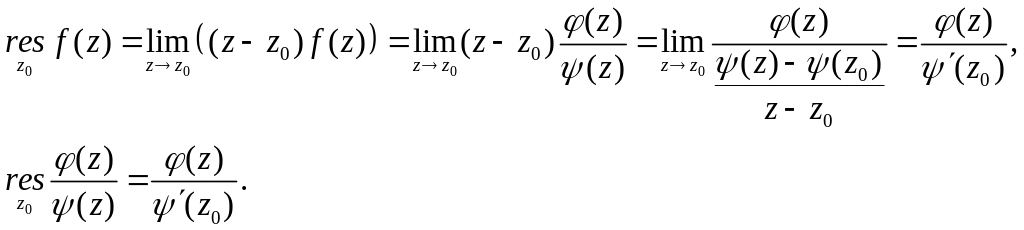
Приклади

1) - полюс 3-го порядку.

.

2) ;

- особливі точки.

Точки - прості полюси

Для суттєво особливої точки тільки лишок .

20. Лишки в нескінченно віддаленій точці

Нехай - аналітична в деякому околі точки і - простий замкнений контур в цій області, всередині якого знаходиться , наприклад, В цьому випадку додатній обхід області, якій належить , є обхід за годинниковою стрілкою і . Нехай є розклад в області і

Приклади

1)

2)

Теорема

Сума всіх лишків однозначної аналітичної функції, що має в розширеній комплексній площині тільки ізольовані особливі точки, дорівнює нулю.

Доведення

має тільки ізольовані особливі точки, отже, їх скінченне число. Інакше множина цих точок мала б граничну точку, та існувала б неізольована гранична точка. Нехай - всі особливі точки , і . Тоді при маємо (1)

Але

(2)

Доведено.

Якщо - правильна точка, то

може не дорівнювати нулю.

Приклад

. Але якщо для - нуль порядку , то