
- •11. Ряд Лорана аналіт.Функції, його єдинственність для анал.Функц.
- •12. Теорема Лорана про розвинення анал.Функції в ряд Лорана
- •13. Ізольовані особливі точки. Класифікація.
- •14. Теорема про правильну точку аналітичної функції.
- •15. Полюси. Необхідна і достатня умова полюса к-го порядку.
- •16. Зв’язок характеру особливої ізольованої точки з виглядом розкладу в ряд Лорана в околі цієї точки
- •17. Характер нескінченно віддаленої особливої точки
- •18. Лишки. Їх зв’язок з інтегралом по замкненій кривій
- •19. Обчислення лишків
- •20. Лишки в нескінченно віддаленій точці
- •21. Застосування лишків для обчислення визначених інтегралів
- •22. Застосування лишків до невласних інтегралів
- •23. Застосування лишків до невласних інтегралів
- •24. Тригонометричні ряди Фур’є
- •25. Абстрактні ряди Фур’є
- •26. Нерівність Коші-Буняковського та теорема Піфагора.
- •27. Основні властивості коефіцієнтів Фур’є. Нерівність Бесселя
- •Нерівність Бесселя
- •28. Поточкова збіжність тригонометричних рядів Фур'є
- •29. Лема Рімана та наслідок з неї.
- •30. Достатня умова збіжності ряду Фур’є в точці.
- •31. Теорема Фейєра та наслідки з неї.
- •32. Зв’язок швидкості спадання коефіцієнтів ряду Фур’є з гладкістю функції
- •33. Теорема про повноту тригонометричної системи
- •34. Перетворення Фур’є, існування, властивості.
- •35. Достатні умови представлення функції в інтеграл Фур’є
- •36. Перетворення Лапласа. Аналітичність перетворення Лапласа.
- •37. Властивоcті перетворень Лапласа
- •38. Диференціювання та інтегрування оригінала та зображення
- •39. Згортка функції. Зображення згортки.
- •40. Обернене перетворення Лапласа. Формула Рімана-Меліна
- •41. Лема Жордана. Формула обернення.
11. Ряд Лорана аналіт.Функції, його єдинственність для анал.Функц.
Розглянемо ряд
![]() (1) Заміна
(1) Заміна
![]() - степеневий ряд, збігається абсолютно
і рівномірно всередині кола
- степеневий ряд, збігається абсолютно
і рівномірно всередині кола
 . Ряд (1) збігається абсолютно і рівномірно
при
. Ряд (1) збігається абсолютно і рівномірно
при

Область збіжності
ряду (1) – це область зовні кола
![]() .
.
Можливі випадки :
1) Якщо
![]() ,
то ряд (1) розбігається в усіх скінченних
точках.
,
то ряд (1) розбігається в усіх скінченних
точках.
2) Якщо
![]() ,
то ряд збігається абсолютно і рівномірно
зовні кола
,
то ряд збігається абсолютно і рівномірно
зовні кола
![]() та розбігається всередині цього кола.
та розбігається всередині цього кола.
3) Якщо
![]() ,
то ряд збігається скрізь, крім самої
точки
,
то ряд збігається скрізь, крім самої
точки
![]() .
.
Отже, в області
збіжності ряд (1) визначає аналітичну
функцію
![]()
При
![]()
![]() можемо вважати, що
можемо вважати, що
![]() аналітична в точці
аналітична в точці
![]() .
.
Означення
Рядом Лорана в точці
називається ряд виду
![]()
Цей ряд розуміють як
суму двох рядів :
![]() і
і
![]() .
Він називається збіжним тоді і тільки
тоді, коли збігаються обидва ці ряди.
.
Він називається збіжним тоді і тільки
тоді, коли збігаються обидва ці ряди.
Перший ряд збігається
при
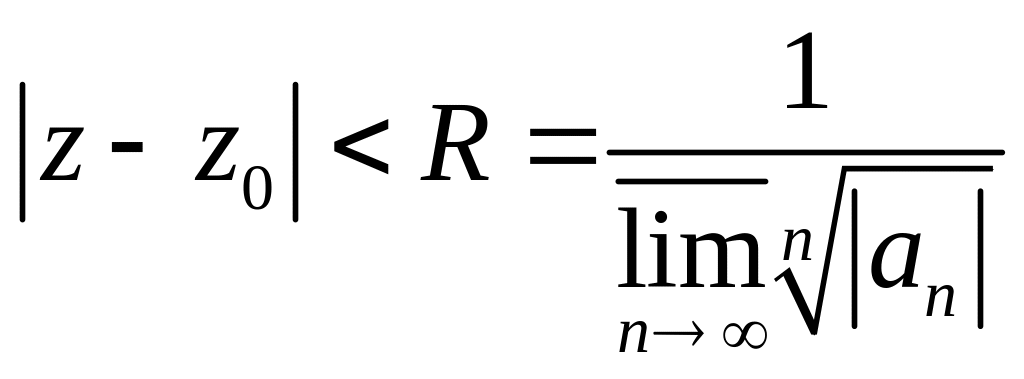 ,
другий – при
,
другий – при
![]() .
Таким чином, ряд Лорана збігається тоді
і тільки тоді, коли
.
Таким чином, ряд Лорана збігається тоді
і тільки тоді, коли
![]() і область збіжності його – це кільце
і область збіжності його – це кільце
![]() .
В цьому випадку обидва ряди збігаються
рівномірно і абсолютно, тоді їх сума –
аналітична функція
.
В цьому випадку обидва ряди збігаються
рівномірно і абсолютно, тоді їх сума –
аналітична функція
![]() ,
(2)
,
(2)
( ).
Визначимо зв’язок коефіцієнтів ряду (2) з його сумою.
Нехай
![]() .
На колі
.
На колі
![]() ряд (2) збігається рівномірно, і він також
буде збігатись рівномірно, якщо його
помножити на обмежену функцію
ряд (2) збігається рівномірно, і він також
буде збігатись рівномірно, якщо його
помножити на обмежену функцію
![]()
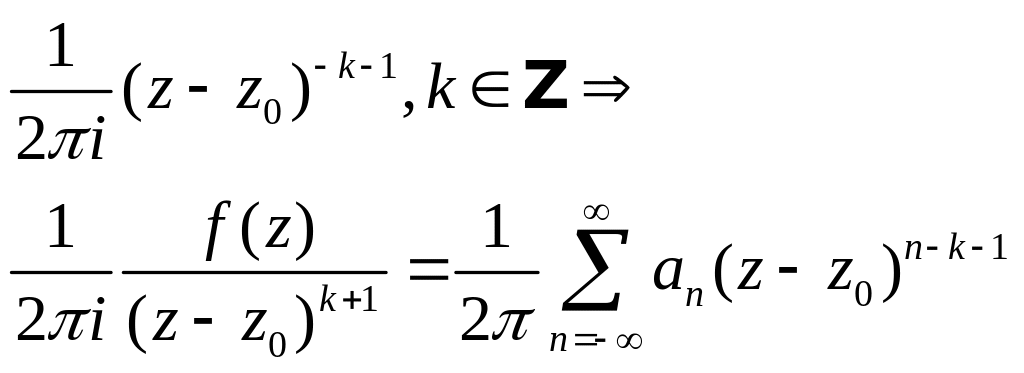
- рівномірно збігається
в точках кола
![]() можна інтегрувати почленно на
можна інтегрувати почленно на
![]() :
:
 (з попередніх лекцій відомо, що
(з попередніх лекцій відомо, що
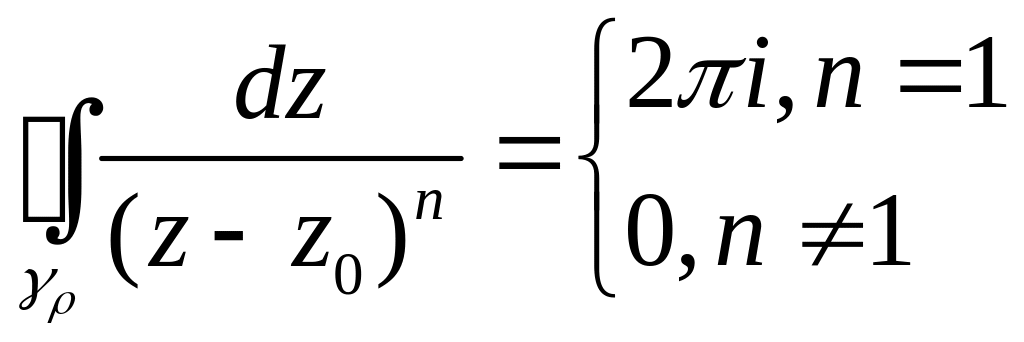 ).
).
В правій частині всі
інтеграли рівні 0, крім інтеграла для
![]() (в цьому випадку
(в цьому випадку
![]() ).
).
Отже,
![]() .
.
Наслідок
Якщо суми двох рядів
Лорана
![]() і
і
![]() ,
що збігаються в кільцях
,
що збігаються в кільцях
![]() відповідно, співпадають на колі
(спільне для
),
то
відповідно, співпадають на колі
(спільне для
),
то
![]() ,
тобто ряди тотожні.
,
тобто ряди тотожні.
Висновок
Розклад в рад Лорана має властивість єдиності.
12. Теорема Лорана про розвинення анал.Функції в ряд Лорана
Будь-яка функція
![]() ,
однозначна і аналітична в області D
(
)
може бути представлена в цьому кільці
збіжним рядом Лорана
.
,
однозначна і аналітична в області D
(
)
може бути представлена в цьому кільці
збіжним рядом Лорана
.
Зауваження
Охоплюються випадки:
1) круг без центра – точки
![]()
2) зовні кола
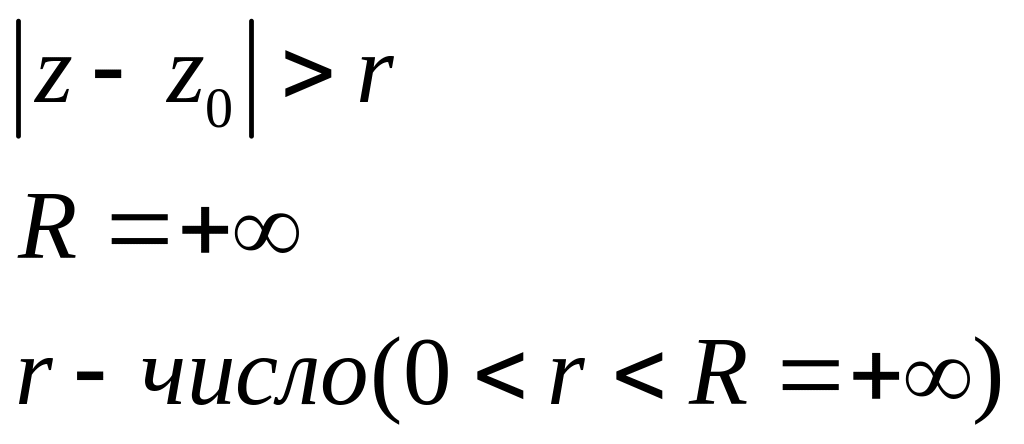
3) вся площина без точки
![]()
Доведення
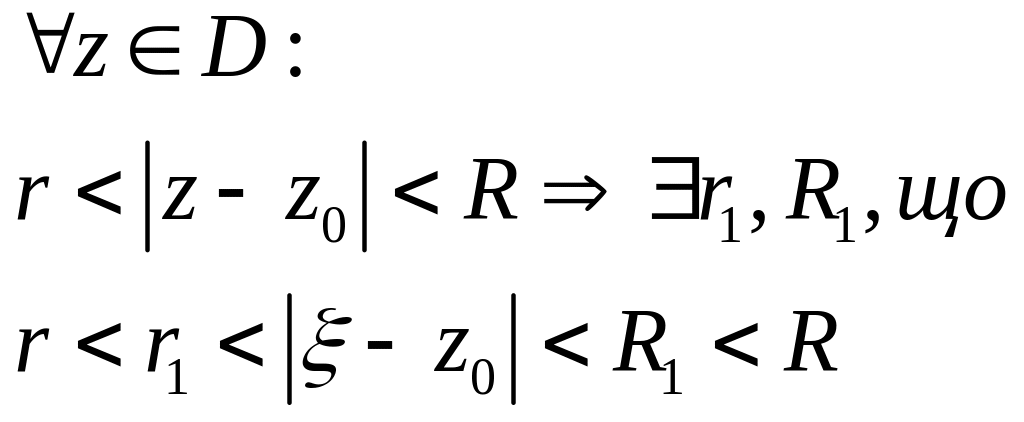
Тоді в області
![]() функція
функція
![]() аналітична. Має місце інтегральна
формула Коші :
аналітична. Має місце інтегральна
формула Коші :
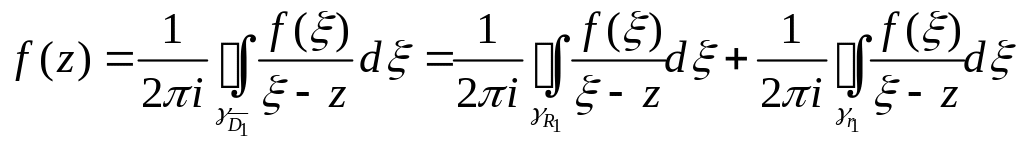 .
.
1) На
![]() маємо
маємо
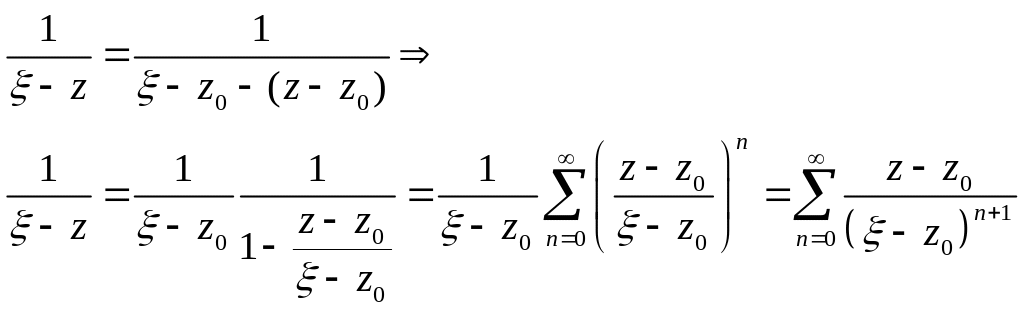
(як сума геометричної
прогресії із знаменником
![]() ).
).
- аналітична на
![]() неперервна, обмежена, тоді на
рівномірно збігається і ряд
неперервна, обмежена, тоді на
рівномірно збігається і ряд
![]() його можна почленно інтегрувати:
його можна почленно інтегрувати:
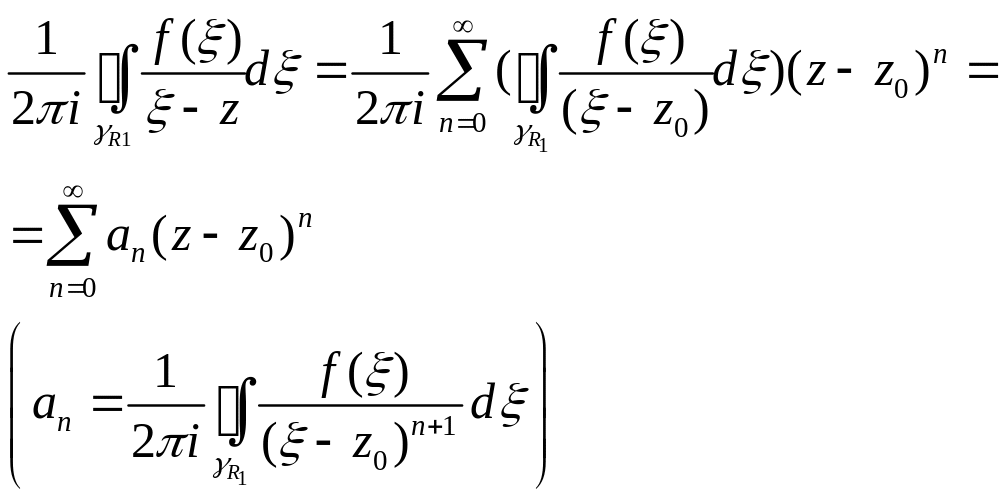
2) На
![]() маємо :
маємо :
![]()
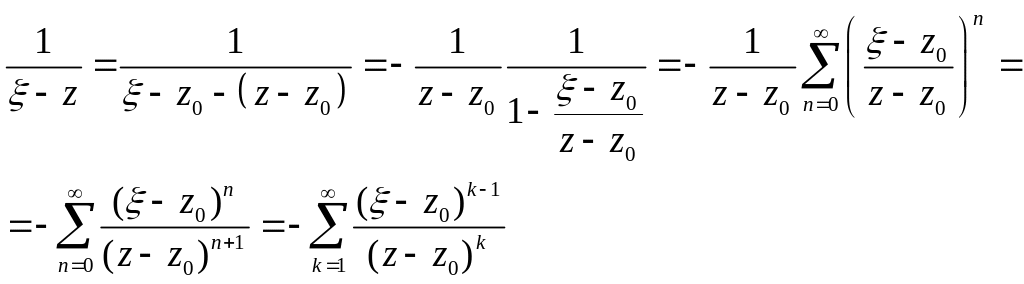
![]() - неперервна, обмежена
в точках
- неперервна, обмежена
в точках
![]() ряд буде збігатися рівномірно і після
множення на
:
ряд буде збігатися рівномірно і після
множення на
:
![]() .
.
Можна інтегрувати на почленно :
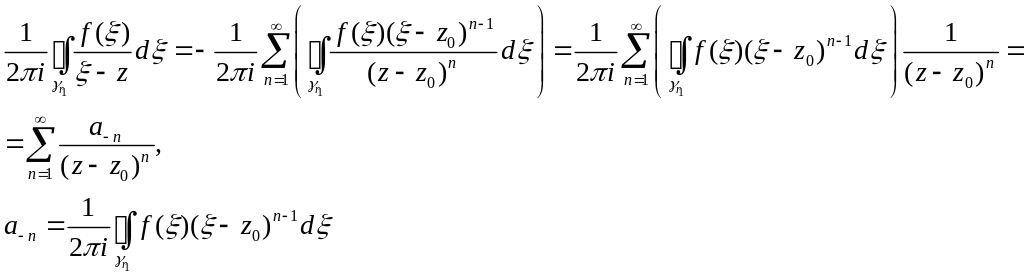
Таким чином, отримали
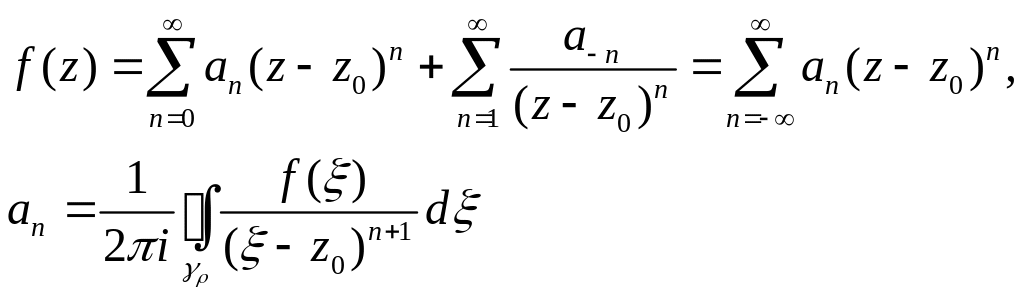
(з теореми Коші для багатозв’язних областей випливає, що
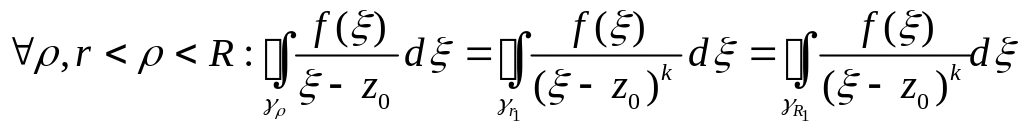 ).
Доведено.
).
Доведено.
13. Ізольовані особливі точки. Класифікація.
Нехай f(z)
– однозначна,
аналітична в деякому околі (можливо,
проколотому) точки
,
![]() .
.
Можливі випадки:
1) Існує скінченна
границя
![]() Тоді, поклавши
Тоді, поклавши
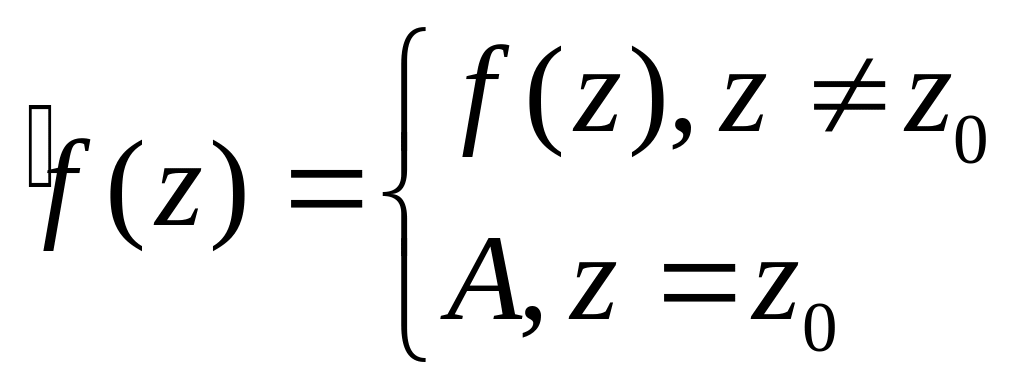 ,
отримуємо аналітичну функцію (в точці
також). Тоді точка
називається правильною
для f(z)
.
,
отримуємо аналітичну функцію (в точці
також). Тоді точка
називається правильною
для f(z)
.
2)
![]()
або
3)
![]() не існує
не існує
В цих випадках називається ізольованою особливою точкою функції f(z) .
Розглянемо ряд Лорана в околі точки :
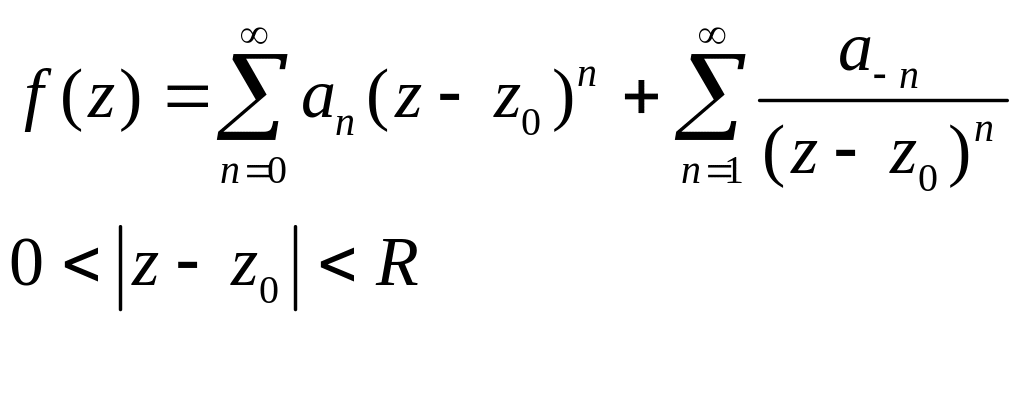 (1)
(1)
(Частина ряду Лорана
з від’ємними степенями
![]() називається
головною частиною, а чистина з невід’ємними
степенями
називається
головною частиною, а чистина з невід’ємними
степенями
![]() називається правильною частиною).
називається правильною частиною).
![]() (2)
(2)
Якщо f(z)
аналятична
і однозначна при
![]() ,
то
буде правильною для
тоді і тільки тоді, коли
обмежена в деякому околі точки
.
,
то
буде правильною для
тоді і тільки тоді, коли
обмежена в деякому околі точки
.
Якщо
- ізольована особлива точка функції
,
то
необмежена в будь-якому околі
![]() ,
і навпаки.
,
і навпаки.
необмежена – має місце два випадки:
1)
![]() точка
називається полюсом
функції
.
точка
називається полюсом
функції
.
2)
не існує
![]() (
(![]() ,
існує) -
називається суттєво
особливою точкою.
,
існує) -
називається суттєво
особливою точкою.
