3. Вычислить .

4. Вычислить .

БИЛЕТ № 11.

1. Преобразование координат вектора при переходе к новому базису.

Пусть в -мерном линейном пространстве выбран базис , и другой, новый, базис . Возьмем произвольный вектор 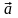из пространства . Его координатный столбец в старом базисе обозначим 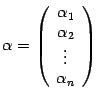, а в новом -- .

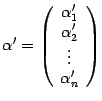Запишем разложения новых базисных векторов по старому базису:

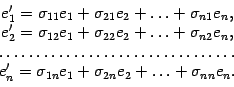
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

Координатные столбцы в старом базисе и в новом базисе связаны формулой где справа стоит произведение матрицы перехода на матрицу-столбец.

Доказательство. Так как  - координатный столбец вектора в новом базисе, то . Заменив векторы их разложениями по старому базису, получим: .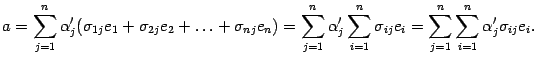

Изменим порядок суммирования 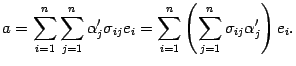Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца будет иметь такой же вид. Следовательно, формула доказана.

2. Теоремы о пределе частного, суммы и произведения.

Если существуют пределы :

Теорема. 1. Предел суммы есть сумма пределов:

Теорема. 2. Предел произведения есть произведение пределов:

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0):

3. Выполнить действия .

1.

2.

4. Вычислить .

БИЛЕТ № 12.

1. Неравенство Коши-Буняковского.

Теорема (неравенство Коши-Буняковского): для любых чисел :

Доказательство: при неравенство верно. Допустим, . Докажем, что

Перепишем это неравенство, частично раскрыв скобки:

.

Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать

Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:

, что и доказывает неравенство Коши-Буняковского.

2. Теорема о сравнении пределом двух функций.

Теорема. Пусть даны две функции и , заданные на , причём при всех выполняется неравенство Тогда из сходимости интеграла от большей функции, , следует сходимость интеграла от меньшей функции, , причём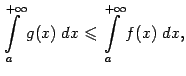 а из расходимости интеграла от меньшей функции, , следует расходимость интеграла от большей функции, :

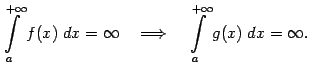
        Доказательство. Поскольку , то функция не убывает (геометрически значение функции равно площади криволинейной трапеции, лежащей над отрезком , а эта площадь, очевидно, не убывает, если увеличивать ). Точно так же не убывает и функция , причём по теореме об интегрировании неравенства получаем: из следует, что

Так как не убывает, то сходимость интеграла означает, что предел при существует и при всех . Поэтому при всех , то есть функция ограничена сверху постоянной . Но мы знаем, что неубывающая ограниченная сверху функция непременно имеет предел при , не больший ограничивающей постоянной: существует предел

По определению, этот предел равен значению несобственного интеграла:

так что сходимость интеграла от меньшей функции доказана, а полученное неравенство означает, что первое утверждение доказано.

Доказательство второго утверждения теоремы сразу следует из первого утверждения по принципу "от противного": предположим, что интеграл от меньшей функции расходится. Если бы утверждение было неверно и интеграл от большей функции оказался бы сходящимся, то вместе с ним сходился бы и интеграл от меньшей функции, вопреки предположению. Значит, второе утверждение теоремы верно.