2. Теорема Коши.
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка , a < < b, такая, что
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке .
Доказательство. Рассмотрим вспомогательную функцию
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка ,
a < < b, такая, что F() = 0.
Т.к.
,
то
А
т.к.
,
то
.
Теорема доказана.
3.
Построить геометрическое место точек
плоскости хОу, задаваемое уравнением
.
Приведём уравнение кривой к каноническому виду:
Уравнение сопряжённой гиперболы.
y
2
-2 0 x
4.
Провести исследование и построить
график функции
.
Функция чётная, симметрична относительно Ох.
y
’
- + - +
y
0
x
y ’’ + - +
y -1 1 x
y
-1
0 1
x
-5
-9
БИЛЕТ № 20.
1. Каноническое уравнение эллипса.
2. Теорема Лагранжа.
Если
функция f(x)
непрерывна на отрезке [a,
b]
и дифференцируема на интервале (а, b),
то на этом интервале найдется по крайней
мере одна точка ,
a
<
< b,
такая, что
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Отношение
равно угловому коэффициенту секущей
АВ.
у
В
А
0 а b x
Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.
Доказательство. Рассмотрим некоторую вспомогательную функцию
F(x) = f(x) – yсек АВ
Уравнение секущей АВ можно записать в виде:
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка , a < < b, такая что F() = 0.
Т.к.
,
то
,
следовательно
Теорема доказана.
3.
Вычислить интеграл
.
4.
Вычислить
.
БИЛЕТ № 21.
1. Каноническое уравнение гиперболы.
2. Производные параметрически и неявно заданных функций.
1. Производная функции, заданной параметрически.
Пусть
Предположим, что эти функции имеют производные и функция x = (t) имеет обратную функцию t = Ф(х). Тогда функция у = (t) может быть рассмотрена как сложная функция y = [Ф(х)].
Т.к.
Ф(х) – обратная функция, то
.
Окончательно получаем:
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
2. Производная неявно заданной функции.
Пусть
дана дифференцируемая функция
,
для которой в некоторой точке
выполнено
неравенство
Тогда
в некоторой окрестности точки
уравнение
определяет,
как мы знаем из теоремы о неявной функции,
некоторую функцию
,
заданную вблизи точки
в
.
Пусть
требуется найти её частные производные
,
.
Это можно сделать, применив формулу
производной сложной функции к функции
которая
тождественно равна 0 в окрестности точки
;
следовательно, и все её частные производные
в точке
обращаются
в 0. Итак, считая параметром, от которого
зависят все аргументы функции
,
переменную
,
где
,
получаем по формуле
:
(производные
равны
0 при
,
),
то есть
откуда
или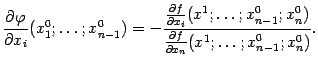
Эта
важная формула позволяет вычислять
производные неявно заданной функции
,
не имея задающего её явного выражения.