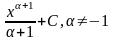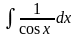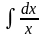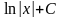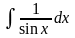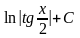- •1. Линейные операции над матрицами. Умножение матриц.
- •2. Неопределённый интеграл. Определение, таблица.
- •3. Найти косинус угла при вершине с в треугольнике авс, если известны координаты вершин треугольника: а (-1;0;4), в (0;-1;3) и с (1;0;4).
- •4. Вычислить интеграл .
- •1. Обратная матрица. Формула для нахождения обратной матрицы.
- •2. Интегрирование рациональных функций.
- •3. Найти угол между векторами и , если а (1;5;8), в (-3;7;2), с (6;4;-1), точка д является серединой отрезка ав.
- •4. Вычислить .
- •1. Интегрирование тригонометрических функций.
- •2. Вектор-функция. Выражение для кривизны в произвольных координатах.
- •3. Найти обратную матрицу к матрице и сделать проверку.
- •4. Вычислить .
- •1. Необходимое условие существования точек локального экстремума функций.
- •2. Интегрирование иррациональных функций.
- •3. Решить систему методом Крамера.
- •4. Исследовать функцию на непрерывность и сделать чертёж её графика.
- •1. Линейно зависимые и линейно независимые системы векторов в пространстве r2 и r3.
- •2. Взаимное расположение прямой и плоскости в пространстве.
- •3. Найти , если , и известны координаты векторов и : , .
- •4. Найти асимптоты функции .
- •1. Базис. Координаты вектора.
- •2. Выпуклость, вогнутость и точки перегиба. Их связь со второй производной.
- •3. Вычислить .
- •4. Вычислить .
- •1. Преобразование координат вектора при переходе к новому базису.
- •2. Теорема о сравнении пределом двух функций.
- •3. Решить систему методом Гаусса.
- •4. Вычислить интеграл .
- •1. Векторное произведение векторов и его свойства.
- •2. Бесконечно малые и бесконечно большие функции и связь между ними.
- •3. Выполнить действия: .
- •4. Вычислить .
- •1. Скалярное произведение и его свойства.
- •2. Первый замечательный предел.
- •3. . Найти обратную матрицу.
- •1. Евклидово пространство. Длина вектора, угол между векторами.
- •2. Второй замечательный предел.
- •3. Решить систему методом Гаусса.
- •4. Вычислить .
- •1. Смешанное произведение векторов и его свойства.
- •2. Определение производной. Таблица производных.
- •3. Привести уравнение к каноническому виду, определить вид кривой и построить её.
- •4. Зависимость у от х задана параметрически . Найти .
- •1. Виды уравнений прямой на плоскости.
- •2. Теорема Ролля.
- •3. Вычислить координаты вектора , перпендикулярного вектору , если .
- •4. Вычислить .
- •1. Виды уравнений прямой в пространстве. Скрещивающиеся прямые.
- •2. Теорема Коши.
- •3. Выполнить действия .
- •4. Найти точки разрыва, исследовать их характер и построить график функции
- •1. Приведение уравнения кривой второго порядка к каноническому виду (без поворотов).
- •2. Свойства определителей n-го порядка.
- •3. Вычислить интеграл .
- •4. Найти точку пересечения прямой и плоскости .
- •1. Правило Лопиталя.
- •3. Вычислить интеграл .
- •4. Найти наибольшее и наименьшее значение функции на отрезке
БИЛЕТ № 1.
1. Линейные операции над матрицами. Умножение матриц.
Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А
=
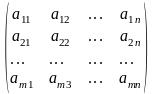
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
С = А + В = В + А.
Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.
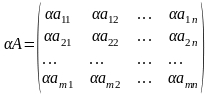
(А+В) =А В
А() = А А
Произведением
матриц называется матрица, элементы
которой могут быть вычислены по следующим
формулам: AB
= C;
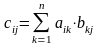 .
.
Из определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц:
1)Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
Очевидно, что для любых матриц выполняются следующее свойство:
AO = O; OA = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Для любых квадратных матриц det (AB) = detAdetB.
2. Неопределённый интеграл. Определение, таблица.
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C.
Записывают:
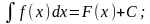
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Интеграл |
Значение |
Интеграл |
Значение |
|||
1 |
|
-lncosx+C |
9 |
|
ex + C |
|
2 |
|
lnsinx+ C |
10 |
|
sinx + C |
|
3 |
|
|
11 |
|
-cosx + C |
|
4 |
|
|
12 |
|
tgx + C |
|
5 |
|
|
13 |
|
-ctgx + C |
|
6 |
|
ln |
14 |
|
arcsin |
|
7 |
|
|
15 |
|
|
|
8 |
|
|
16 |
|
|
|
3. Записать каноническое уравнение прямой, проходящей через точки А (2;-5) и В (4;7). Лежит ли точка С (0;17) на прямой АВ? Ответ обосновать.
Уравнение прямой, проходящей через 2 заданные точки – А и В:

Проверка точка С:
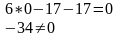
Точка С не лежит на прямой АВ.
4.
Вычислить интеграл
 .
.

БИЛЕТ № 2.
1. Вычисление определителей второго, третьего и n-го порядка.
Определитель второго порядка:
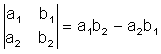
Определитель третьего порядка:
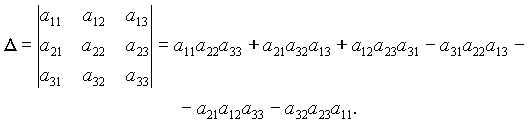
Определитель n-го порядка:

где M1j — определитель квадратной матрицы, полученной из матрицы A вычеркиванием
первой строки и j-го столбца.
2. Вектор-функция. Интегрирование. Натуральный параметр.
Пусть
каждому значению
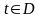 поставлен
в соответствие вектор
поставлен
в соответствие вектор
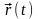 трехмерного
пространства. В этом случае говорят,
что на множестве D
задана векторная
функция.
трехмерного
пространства. В этом случае говорят,
что на множестве D
задана векторная
функция.
Если
в пространстве задана декартова система
координат, то задание вектор-функции
означает
задание скалярных функций x (t),
y (t),
z (t).
Если
 – единичные векторы координатных осей,
то
– единичные векторы координатных осей,
то
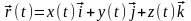 .
.
Для
вектор-функции
,
заданной на отрезке можно составить
интегральные суммы и рассмотреть их
предел при стремлении к нулю максимальной
длины отрезков, на которые разбит отрезок
[a;b].
Этот предел будет называться интегралом
от
по
отрезку [a;b]
и обозначаться
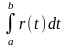 .
Этот предел существует только если
непрерывна
на отрезке [a;b].
На интегралы от вектор-функций
распространяются обычные свойства
интегралов от скалярных функций.
.
Этот предел существует только если
непрерывна
на отрезке [a;b].
На интегралы от вектор-функций
распространяются обычные свойства
интегралов от скалярных функций.
Вектор-функции
широко используются в физике. Так,
скорость
 ,
ускорение
,
ускорение
 ,
сила
,
сила
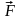 напряженности электрического и магнитного
полей
напряженности электрического и магнитного
полей
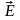 и
и
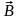 плотность
тока
плотность
тока являются векторными функциями координат.
являются векторными функциями координат.
|

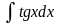
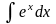

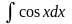
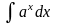
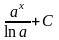
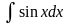
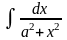
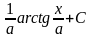
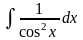
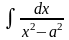

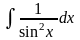
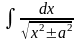


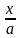 + C
+ C