17) Определение кривизны на участках с трещинами в растянутой зоне.

В этом случае кривизна определяется исходя из второй стадии напряженно деформированного состояния (НДС), т.е. с учетом трещин и упруго пластических свойств бетона. После появления трещин растянутая зона разделяется на участки по трещинам. Длина участков - 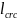(расстояние между трещин,). Над трещинами будут участки сжатой зоны и между трещинами будут тоже участки сжатой зоны(Х₄, Х₅, Х₆).

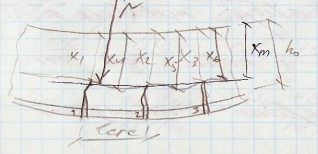
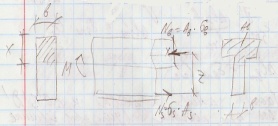
Нейтральная ось при этом будет проходить по волнообразной линии. Напряжения в арматуре и бетоне будут зависеть от места их расположения, т.е. мы их определяем в зоне трещин или между ними. Кривизна при этом будет определяться очень сложно. Для упрощения определения кривизны принимается след допущение:

1Напряжения в бетоне и арматуре, а также их деформации и высота сжатой зоны принимаются равными средним значениям:

2Кривизну определяем по среднему радиусу кривизны.

3Средние деформации арматуры и бетона определяются по их действительным значениям с учетом эмпирических коэффициентов.

4Для средних сечений, рассмотренных между трещинами справедливо гипотеза плоских сечений(сечения до деформации и после остаются плоскими) и закон Гука (а деформации пропорциональны напряжениям и наоборот)

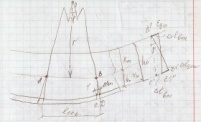
Расстояние между C и D – среднее удлинение арматуры на участке между трещинами

Рассмотрим треугольники AOB, CBD и C`B`D`. Все эти треугольники будут подобны, т.к. стороны параллельны и имеют одинаковые равные φ углы в вершине. У подобных треугольников стороны подобны.

Из подобия треугольников получаем:

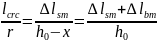
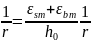- кривизна.

- действительная относительная деформация бетона.

- коэффициент учитывает не только упругие, но и пластические свойства бетона.

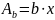– для прямоугольного сечения.

Если сечение не прямоугольное, то

– коэффициент, который учитывает сжатие полки в непрямоугольном сечении.

– момент, при котором определяется кривизна

– плечо пары сил, при котором определяется кривизна

– относительная высота сжатой зоны, при которой определяется кривизна

– коэффициент, учитывающий упруго пластичные свойства бетона; определяется в соответствии со СНиП, как и другие коэффициенты в зависимости от длительности действия нагрузки. При длительной нагрузке кривизна и деформации будут больше, чем при такой же кратковременной. Поэтому:

для длительной нагрузки =0,15 (для тяжелого бетона)

для кратковременной =0,45

- общая площадь растянутой арматуры

- модуль упругости арматуры

- начальный модуль упругости бетона.

- определяются в соответствии со СНиП.

Е сли в элементе кроме момента действуют продольные силы, то они оказывают влияние на кривизну. Это учитывается применением к данной формуле слагаемого соответствующего продольным силам.

Кривизна с учетом продольных сил.

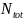– равнодействующая продольных сил.

Чаще всего кривизну определяют для изгибаемых элементов, в которых продольными силами является обжатие бетона напрягаемой арматурой (Р), тогда .

Кривизна уменьшается и прогиб уменьшается при тех же самых нагрузках и размерах.

Определение прогибов для элементов с трещинами в растянутой зоне по их кривизне выполняется аналогично определению ширины раскрытия трещин.

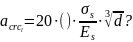
- кривизна и прогиб от непродолжительного действия полной нагрузки.

- кривизна и прогиб от непродолжительного действия постоянной и длительной нагрузки. - продолжительная кривизна и прогиб от действия постоянной и длительной нагрузки.

Е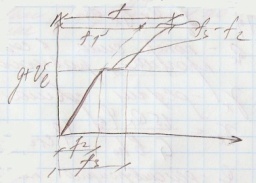 сли в элеменете есть предварительно напряженная арматура, которая обжимает растянутую зону, то кривизна и прогиб уменьшаются. Это учитывается введением кривизны и прогиба и 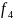, обусловленных усадкой и ползучестью бетона от обжатия его напрягаемой арматурой. Тогда полные кривизна и прогиб будут равны:

Деформации и прогибы в железобетонных конструкциях возникают не только от изгиба, но и от сдвига. Прогиб и деформация сдвига становятся сопоставимыми с прогибом и деформацией изгиба ( ) при соотношении:

где – пролет – высота элемента.

Тогда полная деформация и полный прогиб будут состоять из:

Полный прогиб – это прогиб от изгиба и прогиб от сдвига.

Прогиб от сдвига в общем случае определяется интегралом:

– поперечная сила в сечении Х по направлению прогиба, равного 1

– деформация сдвига.

Где

– действующая поперечная сила в сечении Х

– коэффициент, учитывающий длительность действия нагрузки

- коэффициент, учитывающий влияние трещин на деформацию сдвига

- модуль сдвига для бетона.

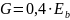(для тяжелого бетона)

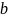- ширина сечения

- рабочая высота сечения

принимаются по СНиП