12. Устойчивость, неустойчивость

Конспект данного параграфа помогли составить И.В. Лурье, А.С. Межакова, А.А. Сируков.

Одним из центральных вопросов, пронизывающих все научное программирование, является проблема устойчивости. Этот термин используется слишком часто и в зависимости от контекста может иметь различные значения. В этом разделе обсудим несколько аспектов проблемы устойчивости в том смысле, как она понимается при численном решении обыкновенных дифференциальных уравнений.

Рассмотрим дифференциальное уравнение второго порядка

у" – 10у' – 11y = 0 (12.1)

с начальными условиями

у(0)=1, y'(0)= –1. (12.2)

Характеристическое уравнение имеет вид

k ² – 10k – 11 = 0. Его корни – k₁ = –1, k₂ = + 11.

Общее решение задачи Коши (12.1), (12.2) имеет вид

y(x) = С₁ e^-x + С₂ e^11x.

Найдем постоянные из начального условия

С₁ = 1, С₂ = 0.

Решением задачи, как легко проверить, является функция у(х) = е^-x. Рассмотрим возмущенную задачу. Предположим теперь, что мы изменили первое начальное условие на малую величину ε. Тогда начальные условия примут вид

y(0)=1 + ε, y'(0) = –1. (12.3)

Как легко убедиться непосредственной подстановкой, решением уравнения с этими начальными условиями будет функция

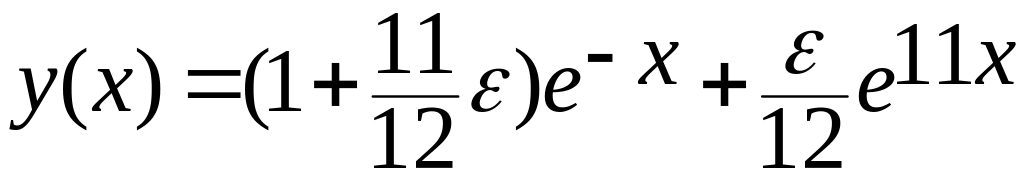. (12.4)

Экспонента с большим показателем приведет к росту решения.

Следовательно, при любом сколь угодно малом ε > 0 второй член в (12.4) приводит к тому, что решение стремится к бесконечности при х → ∞.

Сначала решение задачи (12.1), (12.2) убывает, но, начиная с некоторого значения x, оно начинает расти, т.к. проявляется растущее слагаемое exp(11 x).

Говорят, что решение у(х) =e^11х задачи (12.1)(12.2) является неустойчивым. Это означает, что сколь угодно малые изменения начальных условий могут вызвать сколь угодно большие изменения решения при х→ ∞. В численном анализе такие задачи обычно называют плохо обусловленными (см. раздел 4). В этом случае крайне сложно получить указанное решение численно, поскольку ошибки округления и усечения оказывают такое же влияние, как и изменение начальных условий, и приводят к тому, что решение уходит в бесконечность.

ПРИМЕР 12.1

Напомним, что когда Вас знакомили с теорией ОДУ Вам говорили, что существуют особые точки системы

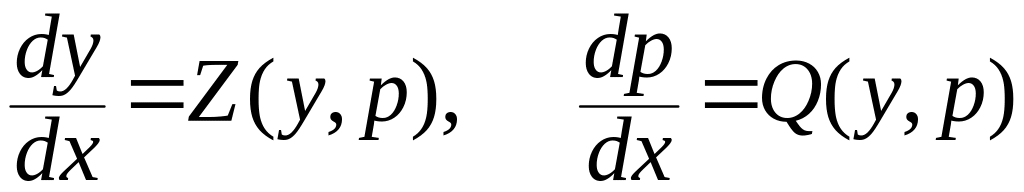или уравнения ,

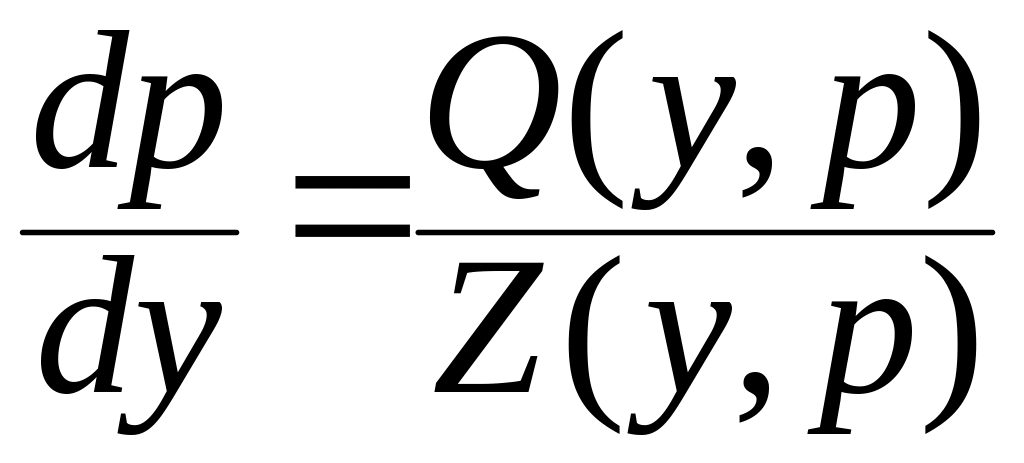где функции непрерывно дифференцируемые. Особой точкой называется такая точка, в которой одновременно обращаются в нуль числитель и знаменатель . Плоскость называют фазовой плоскостью и поведение интегральных кривых на этой плоскости конечно связано с понятиями устойчивости и неустойчивости.

Существует классификация особых точек по собственным числам соответствующей матрицы. Кратко напомним её.

Если корни характеристического уравнения вещественные и одного знака, то эта точка называется узлом.

Если корни характеристического уравнения вещественные и различных

знаков, то такая точка называется седлом.

Если корни характеристического уравнения чисто мнимые, то такая точка называется центром.

Если корни характеристического уравнения комплексные с вещественной частью отличной от нуля, то такая точка называется фокусом.

Некоторые моменты связанные с вырождением и сложными особыми точками мы здесь опускаем и отсылаем читателя к литературе по ОДУ.

Конкретные случаи рассмотрены в других примерах ниже.

ПРИМЕР 12.2

Исследуем особую точку системы, которая следует из уравнения (12.1).

Сделаем замену в (12.1) . Получим систему

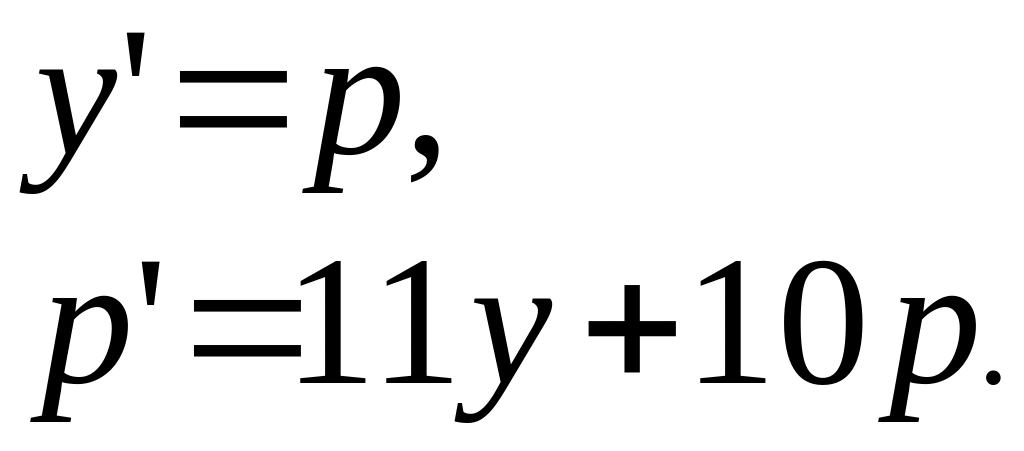
В матричном виде система имеет вид:

Найдем собственные числа данной матрицы. Характеристическое уравнение имеет вид

Посчитаем определитель и получим квадратное уравнение совпадающее с характеристическим уравнением для ОДУ (12.1).

Собственные числа матрицы системы совпадают с корнями характеристического уравнения- это общий факт. .

Если собственные числа матрицы вещественные и разных знаков—это

соответствует особой точке, которая называется « седлом ».

Вычислим собственные вектора . Выпишем систему для первого собственного значения.

. Здесь достаточно перемножить первую строку на столбец вектора и получить первое соотношение . Здесь всегда мы попадаем в случай бесконечного множества решений . Собственный вектор выделяет направление на фазовой плоскости или .

Второй собственный вектор имеет вид . На фазовой плоскости

построены эти прямые и интегральные кривые системы . Они разбегаются от особой точки, что и соответствует неустойчивости решения исследуемой задачи.

Еще более резко неустойчивость может проявиться в нелинейных уравне­ниях. Например, задача

y' = xy (y – 2) , y(0) = 2 (12.5)

имеет решение у(х) ≡ 2, которое является неустойчивым.

Разделим переменные

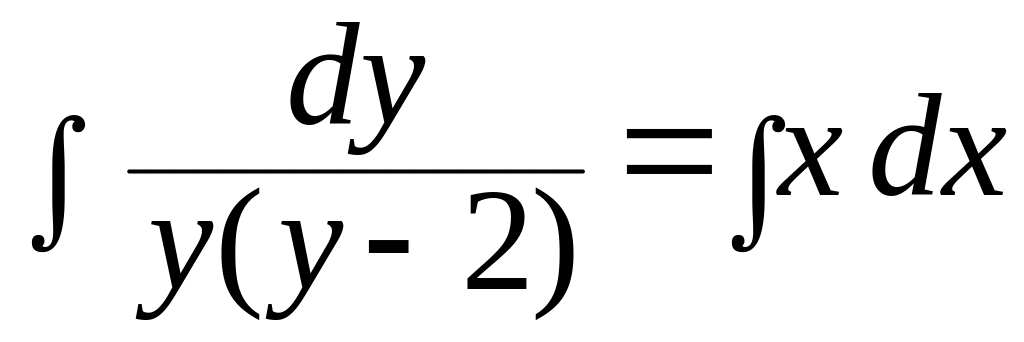. (12.6)

Разложим на простые дроби ( такой способ вычисления интегралов Вам объясняли в курсе математического анализа)

(12.7)

и приведем к общему знаменателю 1 = A (y–2) + B y.

Необходимо, чтобы это выражение было тождественным. Тогда

A = – B, A = –1/2 .

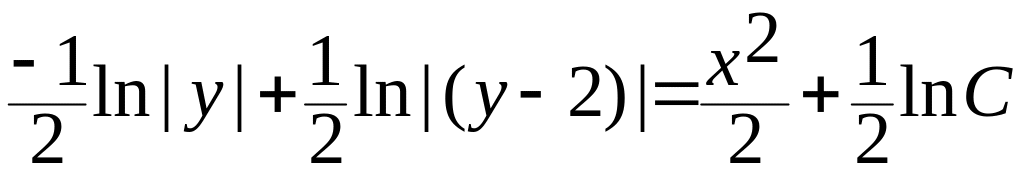, (12.8)

где С  постоянная интегрирования, 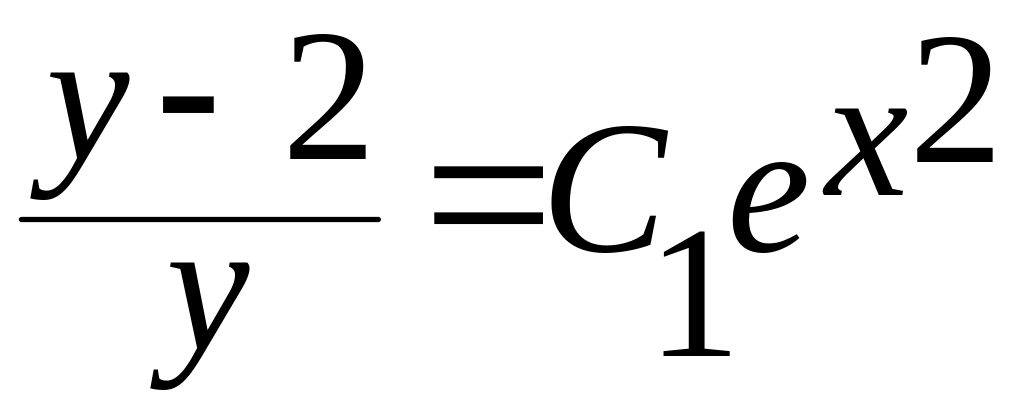. Окончательно получим

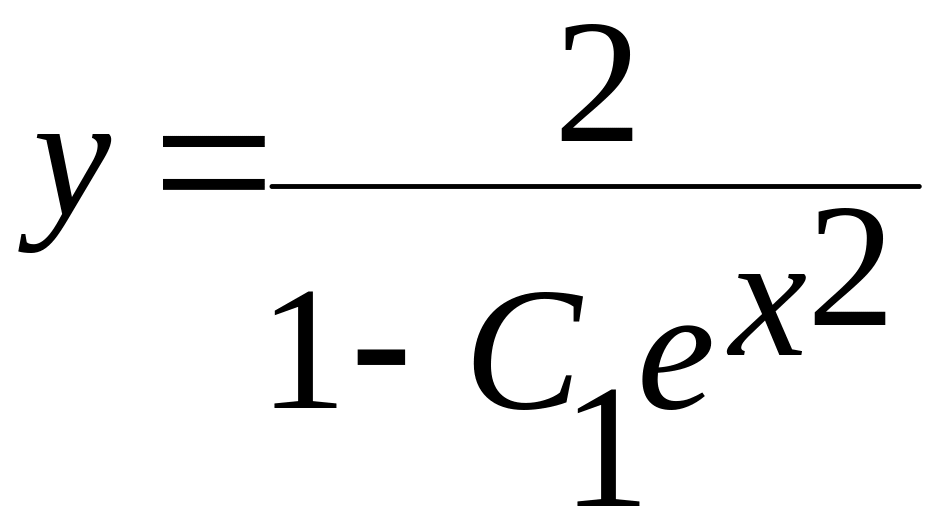. (12.9)

Из начального условия определяем константу С₁=0.

Рассмотрим возмущенную задачу (20.5):

y' = xy (y – 2), y(0) = 2+ ε, ε  бесконечно малое. Найдем новую константу С и решение

. (12.10)

Надо построить графики. Имеем 2 случая:

a) если ε < 0, то решение убывает и стремится к нулю;

б) если ε>0, то в знаменателе имеется точка, в которой он обращается в нуль. Следовательно, решение стремится к бесконечности.

Теория устойчивости сложна и многообразна.

Теория разностных уравнений

Теория разностных уравнений имеет много параллелей с теорией дифференциальных уравнений. Мы кратко обрисуем основные элементы этой теории в случае линейных разностных уравнений порядка m с постоянными коэффициентами. Такие уравнения имеют форму

y_n+1 = a_m y_n + ... + a₁ y_n-m+1 + a₀, n = m-1, m, m+1,..., (12.11)

где а_о,а₁,...,а_n – заданные постоянные.

Однородная часть уравнения (12.11) имеет вид

y_n+1 =a_my_n + … + a₁ y_n-m+1. (12.12)

По аналогии с дифференциальными уравнениями второго порядка (исключая резонансный случай) попытаемся найти для уравнения решения экспоненциального типа. Только в этом случае в качестве экспоненты будем брать выражение у_k = λ^k с некоторой неиз­вестной постоянной λ. Если l удовлетворяет уравнению

λ^m – a_m λ^m-1 – ... – a₁= 0, (12.13)

которое представляет собой характеристическое уравнение для (12.12), то y_k= λ^k действительно является решением (12.12). Если предположить, что все m корней λ₁ , ... , λ_m уравнения (12.13) различны, то последова­тельности λ^k₁ , ... , λ^k_m образуют фундаментальную систему решений и общее решение уравнения (12.12) можно записать в виде

y_k = c_iλ^k_i, k=0, 1,...., (12.14)

где – произвольные постоянные. Если 1    …  0, то, как легко проверить, «частное решение » выражается формулой

(12.15)

Следовательно, общее решение уравнения (12.11) есть сумма (12.14) и (12.15):

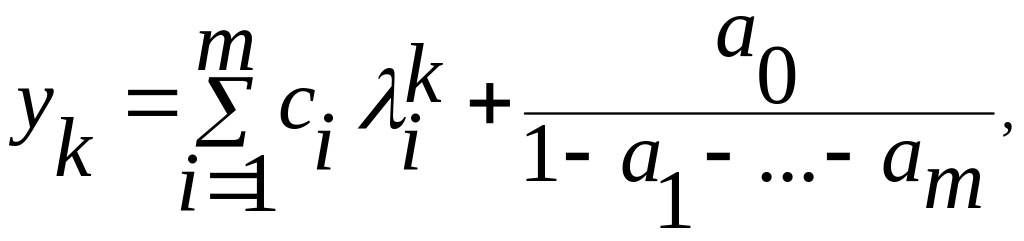
k = 0,1,... (12.16)

Как и в случае дифференциальных уравнений произвольные постоянные в (12.16) определяются из дополнительных условий, накладываемых на решение. Так, если заданы начальные значения

(12.17)

то из (12.18) следуют условия

k = 0,1,...,m 1, (12.18)

представляющие собой систему m линейных уравнений относительно m неизвестных c₁ …,c_m, которую можно использовать для определения значений c_j.

Пример 12.3.

Рассмотрим задачу Коши для ОДУ первого порядка

. (12.19)

Разделим переменные 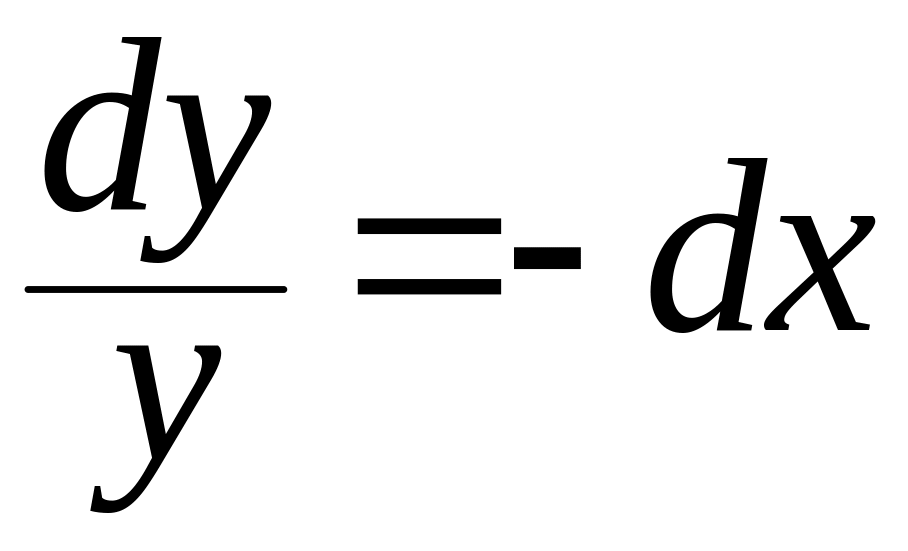, после интегрирования имеем

. (12.20)

Константа интегрирования определяется из начального условия .

Введем сетку (сетка в вычислительной математике- это множество точек) .

Применим метод Эйлера к (12.19). В данном случае получаем

(12.21)

Это разностное уравнение со значением m = 1. В том случае, когда известно точное решение, формулы общей теории разностных уравнений не нужны, можно воспользоваться вторым замечательным пределом:

где - число Эйлера. Это иррациональное число: бесконечная десятичная не периодическая дробь.

Студент: Каким надо выбрать , чтобы предел был выполнен?

В данном случае ответ очевиден :

Т.е. решение разностного уравнения имеет вид

Сделаем проверку. Вычислим:

. (12.22)

Подставим в уравнение (12.21) и убедимся, что это тождество. Т.о., экспоненциальная функция при разностной аппроксимации приближается к степенной функции. При 0 < h < 1 она убывает, следовательно, решение устойчиво. Решим (12.21) с помощью формул общей теории разностных уравнений. Для уравнения (12.21) получаем тот же результат m = 1. Характеристическое уравнение имеет вид ,. Все остальное слагаемые в формулах (12.14) – (12.16) равны 0.

Покажем, что для получения правильного результата численного расчета необходимо, чтобы было устойчиво решение и устойчив сам численный метод.

Пример 12.4

Студент: Предлагаю «подправить» метод Эйлера с целью, значительно улучшить дело.

Давайте рассмотрим многошаговый метод:

. (12.23)

Смотрите и метод многошаговый и шаг двойной. Быстрее считать будет.

Давайте не будем торопиться.

Сравним предлагаемый Вами метод с методом Эйлера. Кажется, что замена шага h на 2h и сдвиг точки на один узел влево не дадут никаких последствий. Однако разберемся в этом, применив метод (12.23) к задаче:

, . (12.24)

Разделим 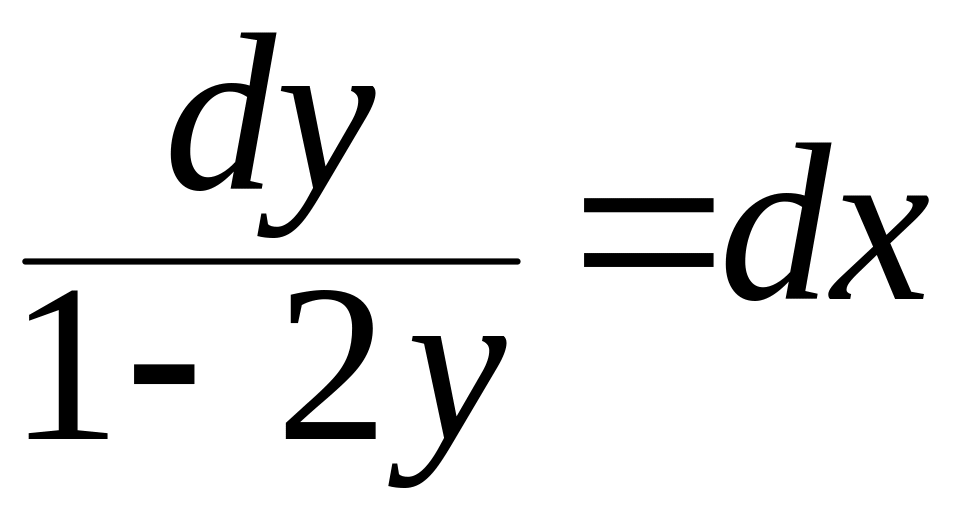, интегрируем .

Тогда решение имеет вид

.

Определяем константу , тогда

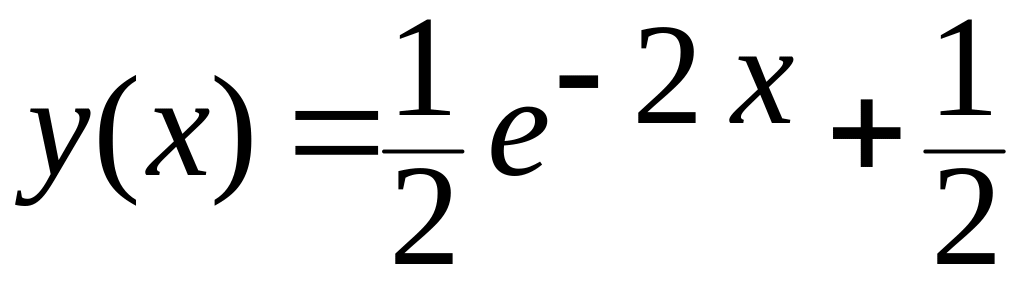. (12.25)

Проверим устойчивость по начальным данным. Рассмотрим возмущенную задачу

, . (12.26)

Найдем новую константу в общем решении .

Получим решение:

. (12.27)

Функция экспоненциально убывает, следовательно, решение устойчиво и никаких «подводных камней» не видно.

Применим предлагаемый метод (12.23) к (12.24) и получим разностное уравнение:

, . (12.28)

Применим теорию разностных уравнений к равенству (21.28), которое перепишем следующим образом:

, , , , . (12.29)

Соответствующее характеристическое уравнение имеет корни

, . (12.30)

Таким образом, для решения уравнения (12.29) по формулам (12.14)  (12.16) получили представление

. (12.31)

Оно позволяет легко определить поведение при . Действительно, при любой фиксированной величине шага h > 0 очевидно, что

, .

Следовательно, при первое слагаемое в выражении (12.31) стремится к нулю, рассмотрим поведение второго слагаемого.

Возьмем, например, последовательность , где k = 1,N. Тогда имеет место последовательность: –2, 4, –8, 16, –32… Члены последовательности растут, меняя знак («скачут»), т.е. последовательность расходится. Аналогично ведет себя второе слагаемое. Так как точное решение (12.25) задачи (12.24) стремится к 0.5 при , ясно, что погрешность приближенного решения стремится к бесконечности и метод (12.23) в применении к задаче (12.24) оказывается неустойчивым. Подчеркнем, что этот рост погрешности никак не связан с ошибками округления, так как формула (12.31) является точным математическим представлением для .

Приведенный пример ясно показывает, насколько важно, чтобы метод был в определенном смысле устойчивым. Определение устойчивости можно сформулировать [5] так:

.

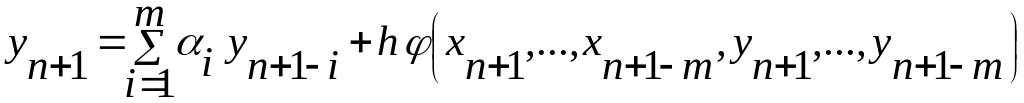(12.32)

Метод (12.32) является устойчивым, если все нули полинома

(12.33)

удовлетворяют условию и любой нуль такой, что , является простым. Если в дополнение к этому

(m – 1) нулей полинома (12.33) таковы, что , то метод (12.32) является строго устойчивым.

Любой метод, имеющий по крайней мере первый порядок точности, должен удовлетворять условию и, следовательно,  = 1 должно быть корнем соответствующего полинома (12.33). В этом случае для любого строго устойчивого метода полином (12.33) будет иметь один нуль, равный 1, а все остальные нули по абсолютной величине будут строго меньше, чем 1. Так как методы Рунге-Кутта являются одношаговыми, то для них . Этот полином не имеет никаких других нулей, кроме , и, следовательно, методы Рунге-Кутта всегда строго устойчивы. В случае m-шагового метода Адамса такого, что остальные m – 1 корней (12.33) равны нулю, такие методы также строго устойчивы.

Для метода (12.29), рассмотренного в Примере 2, полином (12.33) принимает вид и имеет два нуля: +1 и –1. Следовательно, этот метод устойчив, но не строго устойчив. Именно отсутствие строгой устойчивости и приводит к неустойчивому поведению последовательности , порождаемой формулой (12.29). Это можно пояснить следующим образом. Разностное уравнение (12.29) имеет второй порядок (так как в него входят и ) и, следовательно, имеет два фундаментальных решения и , где и – корни характеристического уравнения, определяемые формулами (12.30). Последовательность , получаемая по методу (12.29), строится с целью аппроксимации решения дифференциального уравнения первого порядка (12.24), которое имеет одно фундаментальное решение. Это фундаментальное решение аппроксимируется последовательностью ; последовательность же является «паразитной» и должна быстро стремиться к нулю, чего не происходит.

Однако при любом h>0 и, следовательно, стремится к бесконечности, а не к нулю; именно это и вызывает неустойчивость. Заметим теперь, что при h 0 значения и стремятся к нулям полинома устойчивости (12.24). Действительно, этот полином является предельным при h 0 для характеристического полинома соответствующего уравнения . Понятие строгой устойчивости теперь становится более очевидным. Если все, за исключением одного, нули полинома устойчивости по абсолютной величине меньше единицы, то при достаточно малом h все, кроме одного, корни характеристического уравнения рассматриваемого метода будут по абсо­лютной величине меньше единицы. Следовательно, степени этих корней, являющихся "паразитными" фундаментальными решениями разностного уравнения, будут стремиться к нулю и не приводить к возникновению неустойчивости.

Теория устойчивости, которую мы только что обсудили, касается, по существу, устойчивости в пределе при h 0 .