10. Численные решения. Одношаговые методы.

МЕТОД ЭЙЛЕРА. МЕТОД РУНГЕ-КУТTА

Конспект данного параграфа помогли составить А.Ю. Скавронский, П.В. Рощин.

Теперь рассмотрим задачи Коши для систем обыкновенных дифференциальных уравнений (далее ОДУ ) в общей постановке:

Студент: А что, бывают уравнения необыкновенные, волшебные ?

Нет. Уравнение называется обыкновенным, если имеет место только одна независимая переменная .

(10.1)

(10.2)

Здесь − заданные функции, − независимая переменная, − заданные начальные условия. Надо найти функции , являющиеся решением задачи (10.1) − (10.2) на отрезке . Для простоты изложения в дальнейшем ограничимся одним уравнением

(10.3)

с одной неизвестной функцией и начальным условием

(10.4)

Рассмотренные ниже методы легко распространяются на системы вида (10.1).

Хотя решение некоторых задач Коши может быть найдено аналитически, (выписано авторучкой на листе бумаги ) во многих случаях, в том числе для большинства задач, представляющих практический интерес, такой путь оказывается невозможным. Цель этого и нескольких следующих параграфов настоящей главы состоит в описании способов построения приближенного решения задачи Коши с помощью численных методов, в частности, конечно-разностных методов.

Первый шаг на пути численного решения состоит в разбиении отрезка на конечное число частей введением узловых точек . Хотя неравномерное разбиение отрезка не ведет к каким-либо особым трудностям, для простоты изложения и анализа будем предполагать, что узловые точки делят отрезок на равные отрезки. Если обозначить через расстояние между узлами (шаг сетки), то и , где  (целое) число отрезков разбиения. В дальнейшем будем через обозначать значение точного решения (10.3) в точке , а через  соответствующее приближенное значение, построенное с помощью рассматриваемого численного метода.

Введем сетку:

.

Вероятно, простейшей численной схемой является метод Эйлера, который определяется формулами

(10.5)

Вывод метода Эйлера очевиден. Из разложения Тейлора функции в окрестности точки имеем:

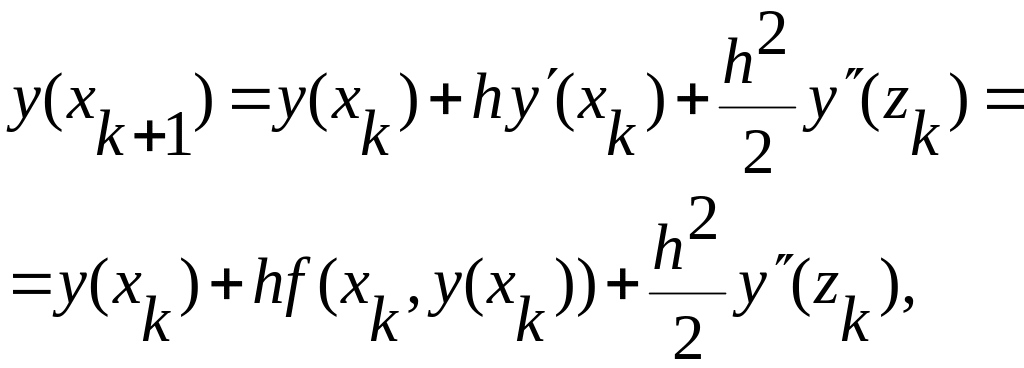(10.6)

где лежит внутри отрезка . Мы всегда будем считать, что все выписываемые производные действительно существуют. Если производная ограничена, а шаг мал, то можно отбросить последний член и, используя обозначение в смысле «приближенно равно», написать

Это и служит основой для (10.5). Геометрический смысл метода Эйлера заключается в аппроксимации решения на отрезке отрезком касательной, проведенной к графику решения в точке .

Метод Эйлера очень прост для реализации на ЭВМ: на шаге вычисляется значение , которое затем подставляется в (10.5). Таким образом, все необходимые операции по существу сводятся к вычислению

Как видно из расчетов применения метода, численное решение сильно отличается от точного и главный вопрос при использовании метода Эйлера или любого другого численного метода состоит в оценке точности приближенных значений . Вообще говоря, существует два источника погрешности этих приближений:

а) ошибка дискретизации, возникающая в результате замены дифференциального уравнения (10.3) разностной аппроксимацией (10.5);

б) ошибка округления, накопившаяся при выполнении арифметических операций по формулам (10.5).

Поскольку анализ общей ошибки, возникающей по этим двум причинам, очень сложен, рассмотрим предельную ситуацию.

Отбросим ошибки округления. Сейчас будем считать, что значения в (10.5) вычисляются точно, так что погрешности обусловлены только ошибкой дискретизации. Введем величину

, (10.7)

называемую глобальной ошибкой дискретизации (иногда эту величину называют глобальной ошибкой усечения). Отметим, что зависит от величины шага h, поскольку предполагается, что приближения вычисляются при заданном значении . Интуитивно ожидаем и определенно надеемся, что при уменьшении ошибка дискретизации будет убывать и, в частности, при стремлении к нулю также будет стремиться к нулю.

Мы не будем здесь давать полный анализ глобальной ошибки дискретизации, а удовлетворимся лишь тем, что покажем, как такой анализ обычно проводится. Во-первых, предположим, что точное решение имеет на отрезке ограниченную вторую производную :

(10.8)

Далее рассмотрим величину

(10.9)

которая называется локальной ошибкой дискретизации метода Эйлера в точке x и служит мерой того, насколько разностная аппроксимация отличается от . Предположим теперь, что равно значению точного решения . Тогда разность между аппроксимацией по Эйлеру и точным решением выражается формулой

(10.10)

Таким образом, умноженная на локальная ошибка дискретизации равна ошибке на одном шаге метода Эйлера, стартовавшего с точного решения.

Обычно нас интересует максимум по , так что определим локальную ошибку дискретизации метода Эйлера как

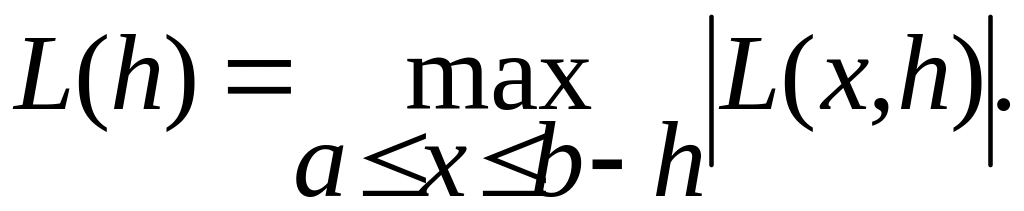(10.11)

Отметим, что величина зависит как от величины шага , так и от вида правой части дифференциального уравнения и от отрезка . Однако здесь выделена явно только зависимость от , поскольку в предложении (10.8) с помощью разложения Тейлора, аналогично (10.6), можно получить оценку

(10.12)

Здесь воспользуемся стандартным обозначением (символ Ландау) для величины, стремящейся к нулю при с той же скоростью, что и . Напомним, что в общем случае говорят, что функция равна , если при величина ограничена.

Задача теперь состоит в том, чтобы связать локальную ошибку дискретизации с глобальной ошибкой дискретизации. Если обозначить ошибку через , то согласно (10.5) и (10.10), получим

(10.13)

Предположим теперь, что функция имеет ограниченную частную производную по второй переменной:

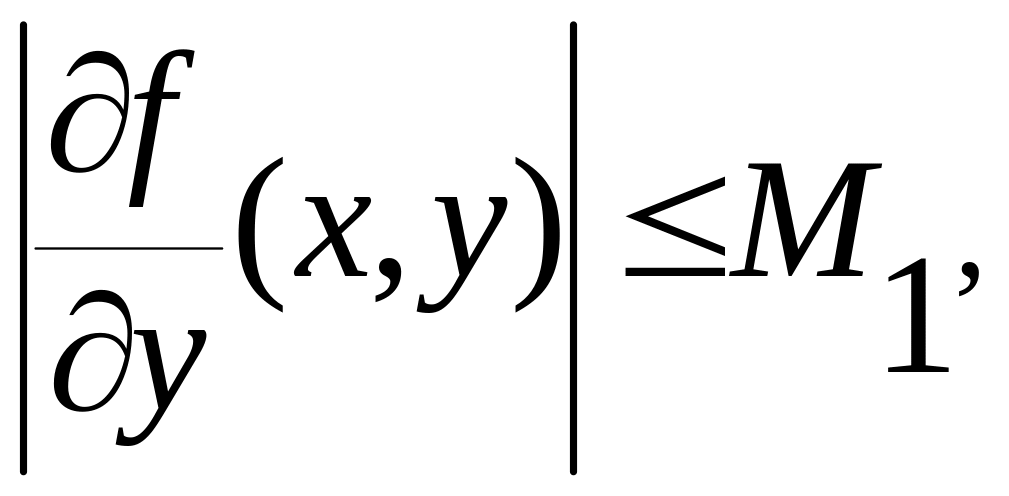
(10.14)

Тогда по теореме Лагранжа о среднем значении при некотором имеем

Используя эту оценку и заменяя на , из формулы (10.13) получим оценку

(10.15)

Полагая здесь и раскрывая последовательность в (10.15), получаем оценку

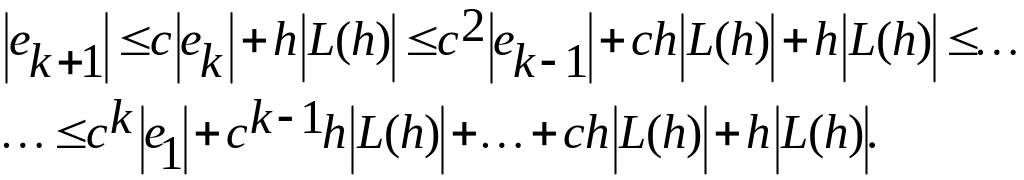(10.16)

Справедлива следующая

Т е о р е м а 2 (ошибка дискретизации метода Эйлера). Если функция f(x,y) имеет ограниченную частную производную по второй переменной и если решение задачи (10.3) — (10.4) имеет ограниченную вторую производную, то глобальная ошибка дискретизации метода Эйлера Е(h) = О(h).

Анализ показывает, что глобальная ошибка дискретизации есть О(h). Это обычно выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является ожидание того, что при уменьшении h приближенное решение будет все более точным и при стремлении h к нулю будет сходиться к точному решению с линейной скоростью по h; т.е. ожидается, что при уменьшении шага h вдвое ошибка уменьшится примерно в 2 раза.

Пример 1.

Рассмотрим задачу Коши для уравнения

y¹=y,_y(0)=1, (10.17)

точное решение которого есть у(х)=е^х.

Объясним наиболее подробным образом, как получено это решение. Запишем производную 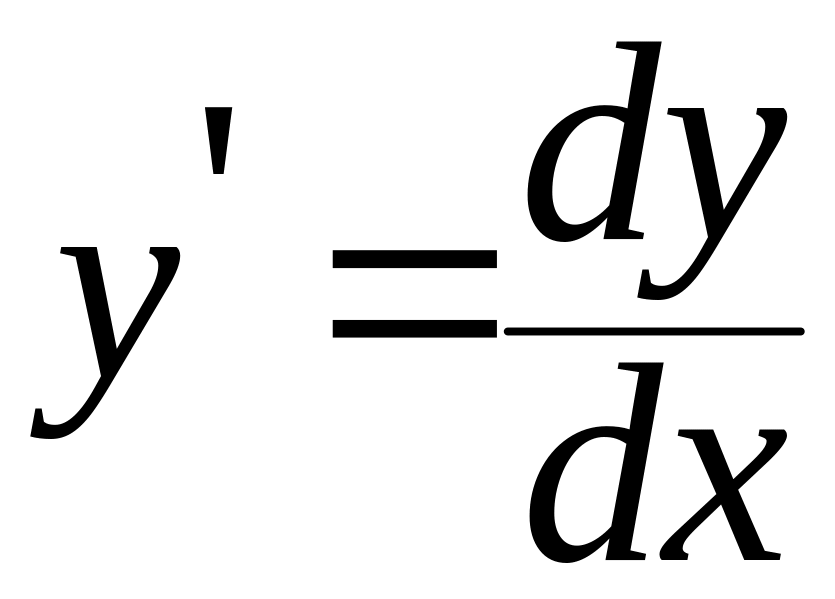. Тогда получим уравнение Далее разделим переменные. В одну сторону переносим выражения содержащие , а в другую сторону переносим выражения содержащие . (В.Г. Данилов любил приговаривать: Надо разделить. Отдельно мухи, отдельно котлеты.) Получим выражение 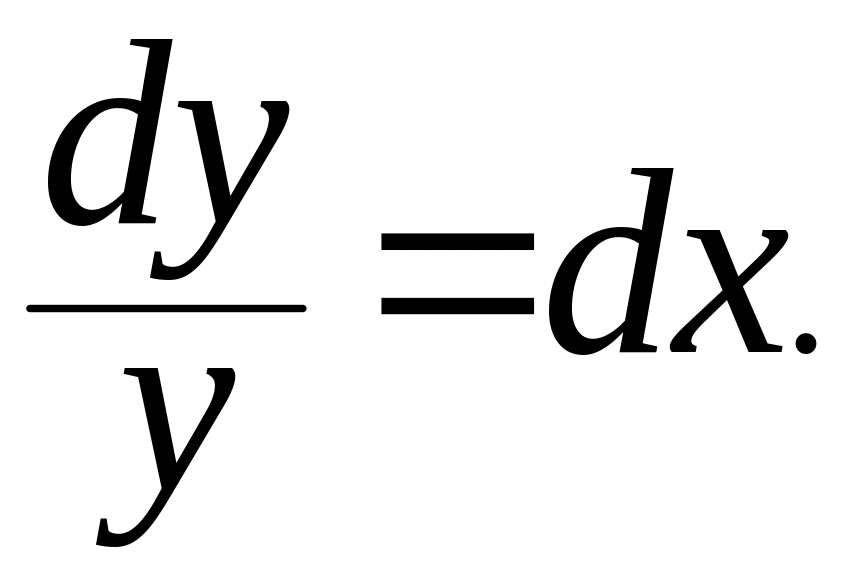Далее интегрируем 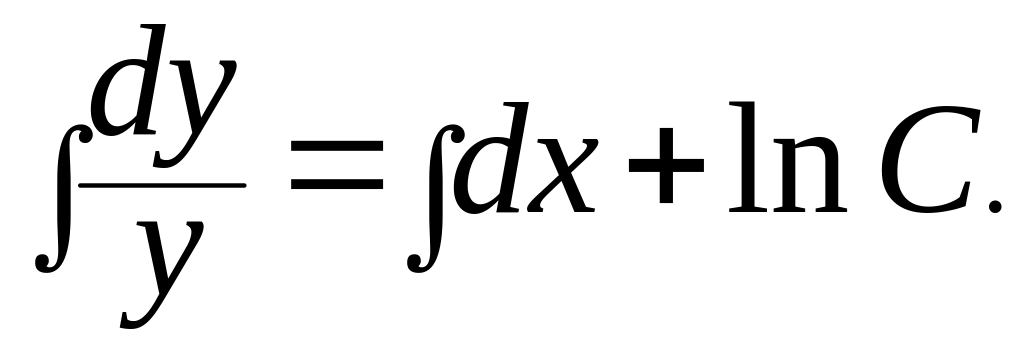Далее получим Константа интегрирования

записана в виде логарифма для удобства. Далее производим потенцирование, то есть переходим от логарифмических к показательным функциям. Получим

. Далее подставляем начальное условие . Таким образом, определяется константа интегрирования.

Рассмотрим сетку c шагом h. Из (10.17) по методу Эйлера следует разностное уравнений .

Его точное решение имеет вид . Так как h > 0, то это выражение растет.

Рассмотрим возмущенную задачу Коши (10.17):

, где ε – бесконечно малая величина. Тогда решение имеет вид .

Вычислим разность . Показательная функция растет быстро, и малая константа не может его ограничить. Таким образом, это решение неустойчивое. Более подробно вопросы устойчивости обсуждаются в следующих разделах.

Очень медленная сходимость при уменьшении h, которая характерна для методов первого порядка, служит препятствием для их использования. Значительная часть остального материала этого раздела посвящена изучению других методов, погрешность которых при стремлении h к нулю убывает с более высокой скоростью. В качестве примера построения одного из таких методов мы рассмотрим модифицированный метод Эйлера, определяемый формулой

y_к+1=y_к+h f(x_к+1, y_к+h f(x_k, y_k)). (10.18)

Обратите внимание на то, что функцию f(x_k,, y_k) в методе Эйлера y_k+1 = y_k+ h f (x_k, y_k) просто заменили на

f (x_k , y_k+h f (x_k , y_k)).

Метод Эйлера известен также как метод Рунге-Кутта второго порядка и имеет локальную ошибку дискретизации O(h²). Наиболее распространенным методом Рунге-Кутта является классический метод четвертого порядка, задаваемый формулой

(10.19)

где

F₁=f(x_k, y_k), F₂=f(x_k + ),

.

Здесь f(x_k, y_k) в отличие от метода Эйлера заменено на взвешенное среднее значение f, вычисленное в четырех различных точках.

В следующем разделе будут рассмотрены методы, которые используют информацию, полученную не только на одном предыдущем шаге, а на многих (не только y_k, но и y_k-1, y_k-2 и т.д.). В настоящем разделе мы имеем дело с методами, зависящими только от y_k и не использующими никаких предыдущих значений. Такие методы называются одношаговыми и могут быть представлены в общем виде как

y_k+1 = y_k+h (x_k, y_k) (10.20)

с соответствующей функцией φ. В случае метода Эйлера функцией φ является сама f, в то время как для метода обобщающего модифицированный метод Эйлера функция φ имеет вид

φ(x,y)= [ f(x, y) + f(x+h, y+h f (x,y))]. (10.21)

Метод Рунге-Кутта четвертого порядка (10.19) тоже является одношаговым, и соответствующая функция φ может быть записана в виде аналогичном (10.21).

Для любого одношагового метода (10.21) определим локальную ошибку дискретизации аналогично методу Эйлера соотношением

(10.22)

где, как и раньше y(x)  точное решение дифференциального уравнения.

Если для данной функции φ окажется, что L(h) = o(h^p) при некотором целом p, то при соответствующих предположениях относительно функций φ и f можно показать, что глобальная ошибка дискретизации будет также порядка р по h, т.е.

. (10.23)

Порядок метода (10.20) определяется как целое р, для которого L(h) = О( ). Такое определение порядка является некоторым утверждением о свойствах самого метода. При этом предполагается, что решение дифференциального уравнения у имеет ограниченные производные до определенного порядка. Например, для метода Эйлера мы показали, что р=1 в предположении (10.10). Как будет продемонстрировано ниже, для других методов может потребоваться ограниченность производных решения и функции f более высокого порядка.

Сравнительно несложно показать, что локальная ошибка дискретизации модифицированного метода Эйлера есть О(h²), но мы получим это как следствие более общего анализа, который служит основанием для методов Рунге-Кутта.

Студент: Можно этому факту дать геометрическую интерпритацию?

Конечно.

Здесь можно пояснить следующее: в методе Эйлера мы ориентируемся по касательной к графику функции в данной точке и получаем ошибку O(h). Если подобрать коэффициенты рядов Тейлора, подправить их так, чтобы получилась секущая графика функции, проходящая через данную точку, то ошибка будет меньше.

Давайте рассмотрим функцию φ, определяемую соотношением

Мы хотим выбрать константы с₁, с₂ и с₃ так, чтобы максимизировать порядок одношагового метода (10.20). Т.е. хотим найти наилучшую определяемую константами с₂ и с₃ линейную комбинацию двух значений f, и найти в какой точке интервала при этом следует вычислять второе значение f, что задается константой с_1.

Разложим функцию φ в ряд Тейлора по двум переменным в окрестности точки (x, y).

Разлагая сначала по переменной х, получаем

где f(x, y) обозначено через f, а частные производные по х  через f_x и f_xx. Воспользовавшись теперь разложением по y, где все встречающиеся частные производные вычислены в точке (x, y), имеем

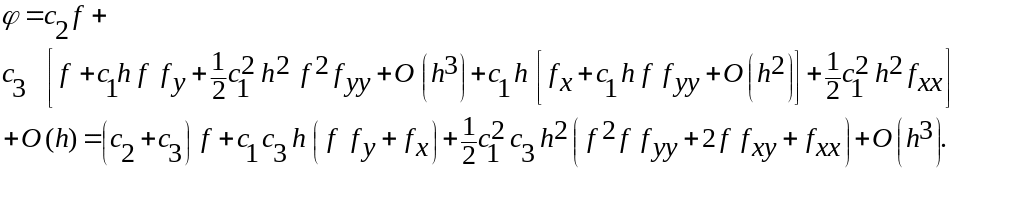
(10.24)

С другой стороны, для точного решения дифференциального уравнения y(x) имеем

(10.25)

Объединяя теперь (10.24) и (10.25), получаем

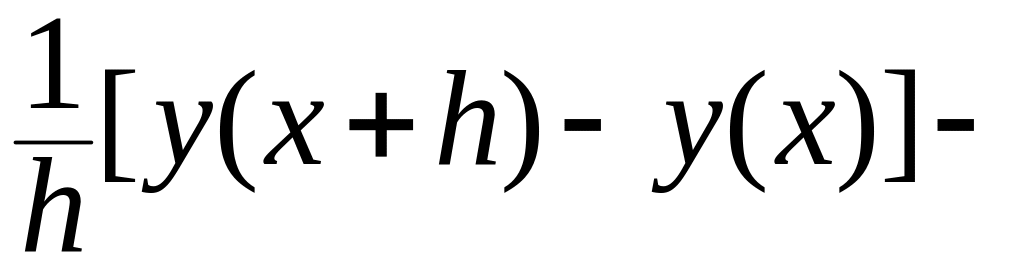φ(x, y(x(x)) =

(f f_y+f_x)+

+ (  ) (f²f_yy+2ff_xy+f_xx)+ (f_x f_y+ )+О(h³).

(10.26)

Если мы потребуем, чтобы

с₂ + с₃ = 1, с₁с₃ = ½, (10.27)

то первые два члена в (10.27) обратятся в нуль для любой функции f. Однако член в общем случае не будет тождественно равен нулю. Так что, как бы мы ни выбирали константы, самое большое, что мы можем иметь

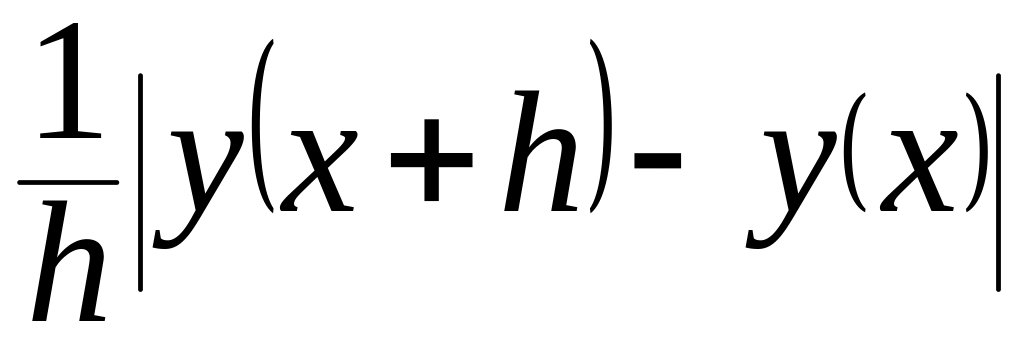– φ (x, y(x)) = О(h²), (10.28)

что и будет выполняться всякий раз, когда удовлетворены условия (10.28) и все необходимые производные ограничены. Таким образом, L(h) = О(h²) и все методы, выделенные условием (10.28),

имеют второй порядок.