Лекция 28 Типы возбуждения и механические характеристики двигателей постоянного тока

В зависимости от способа подключения обмотки возбуждения ДПТ делятся на двигатели независимого, параллельного, последовательного и смешанного возбуждения. В двигателях независимого возбуждения обмотка возбуждения питается от отдельного источника.

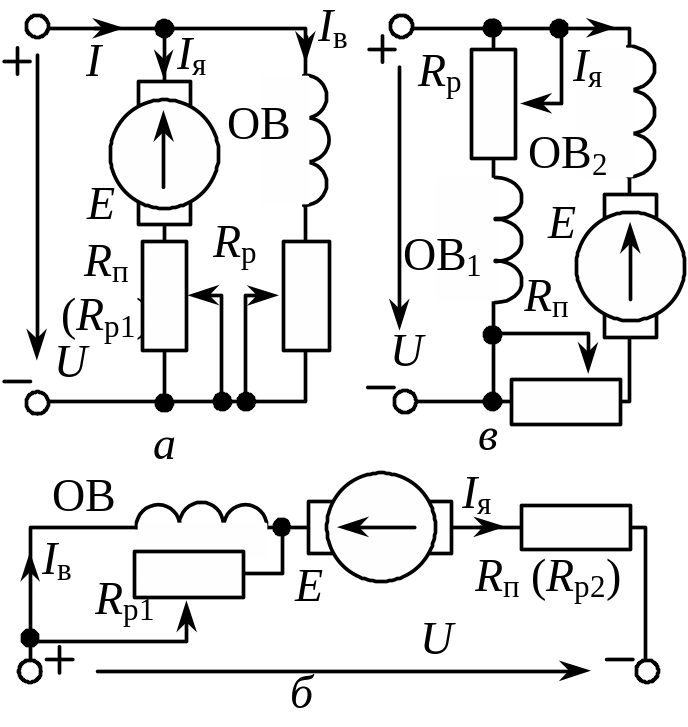
Схемы ДПТ с различны­ми типами возбуждения: а – парал­лельным; б – последовательным; в – смешанным

Основными уравнениями двигателя постоянного тока являются:

уравнение противоЭДС:

Е = С_еФn

уравнение электромагнитного момента;

М = С_мФI_я

уравнение цепи якоря;

Е = U - I_яR_я

уравнение динамики.

М = Jdω/dt + М_с

Важную роль в анализе двигателей играет механическая характеристика – зависимость частоты вращения n от момента M на валу при U, I_в = const.

ДПТ с независимым и параллельным возбуждением имеют общее свойство: ток возбуждения не зависит от тока якоря. Пренебрегая реакцией якоря, можно считать, что и поток Ф у них не зависит от нагрузки (момента М_с). Поэтому свойства и характеристики этих ДПТ идентичны, далее будем упоминать только ДПТ с параллельным возбуждением.

Из уравнений противоЭДС и цепи якоря выражаем частоту вращения якоря:

n = U/С_еФ – I_яR_я)/ С_еФ

Выразив I_я из формулы электромагнитного момента получаем механическую характеристику ДПТ с параллельным возбуждением:

n = (U/ С_еФ) – (МR_я/C_eC_мФ²)

которая получена из статических уравнений и задает связь между n и M в установившемся режиме (при M = M_с). Механическую характеристику называют естественной, если она получена для двигателей без реостатов в цепях якоря и возбуждения при U = U_ном, Ф = Ф_ном. Естественная характеристика является прямой. В режиме холостого хода M = M_с = 0, поэтому первое сла­гаемое в определяет частоту идеального холостого хода

.

В момент пуска двигателя n = 0 и пусковой момент

.

От коэффициента K_н = –R_я/(C_eC_мФ²) зависит угол наклона прямой.

У двигателей средней и большой мощности сопротивление якорной обмотки R_я мало (десятые и сотые доли Ом), пусковой момент велик, а коэффициент K_н мал. Естественная характеристика имеет малый наклон, поэтому с изменением нагрузки частота n изменяется незначительно. Характеристики такого типа называют «жесткими».

На рис. приведена механическая характеристика n = f(M_с) механизма на валу ДПТ. В установившемся режиме M = M_с, рабочая точка А лежит на пересечении характеристик. Обычно точку номинального режима организуют близко к точке холостого хода: n₀ – n_ном = 3¸7% от n₀.

Двигатели с последовательным возбуждением. Для получения механической характеристики полагаем, что в цепях возбуждения и якоря реостаты отсутствуют и I_я = I_в. При слабо насыщенной магнитной цепи можно допустить, что Ф ≈ KI_в = KI_я, где K = const. Подставив Ф в, получим M = C_мKI_я²; I_я = . Выразив n и подставив I_я, получим

n =E/C_eФ = U – R_яI_я/C_eКI_я

Механическая характеристика ДПТ с последовательным воз­ буждением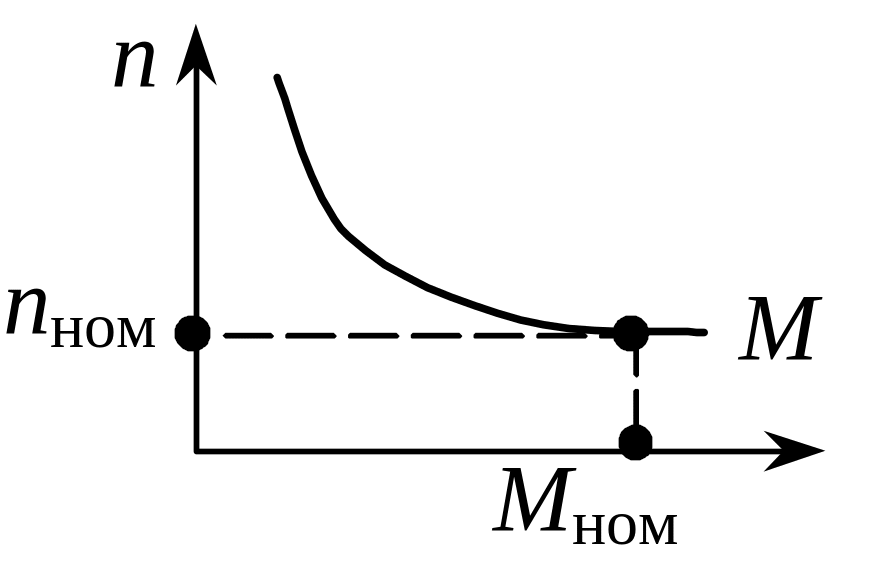

Механическая характеристика ДПТ с последовательным возбуждением нелинейна, является «мягкой», что свиде­тельствует об очень большом пусковом моменте. Из характеристики видно, что запрещается работа (пуск) двигателя без нагрузки (M_с = 0) или с очень малой нагрузкой (M_с << M_ном), так как в результате недопустимо большого нарастания частоты вращения (двигатель идет «в разнос») наступает аварийное разрушение двигателя.

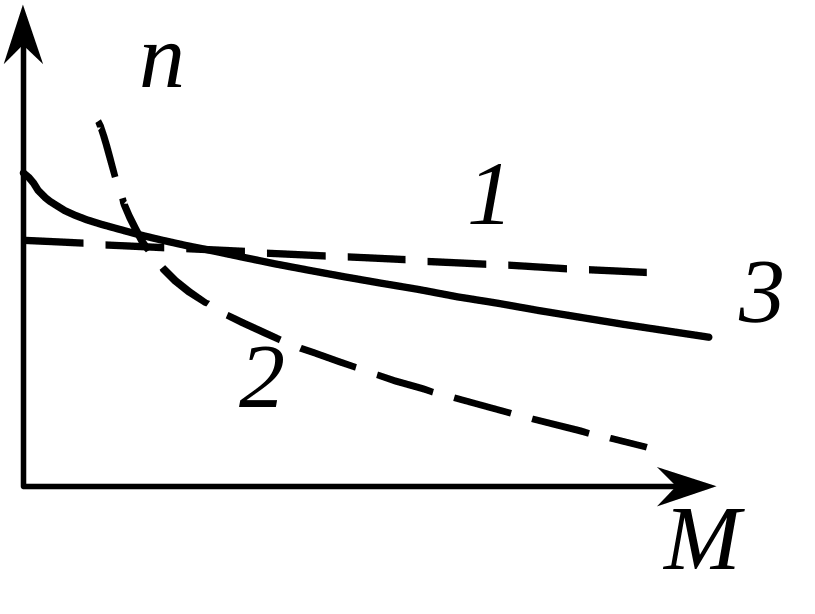
Двигатель со смешанным возбуждением. Наличие параллельной и последовательной обмоток возбуждения у двигателя приводит к тому, что механическая характеристика (кривая 3 на рис. ) располагается между характеристиками ДПТ с параллельным возбуждением (кривая 1) и ДПТ с последовательным возбуждением (кривая 2). Двигатель с такой характеристикой обладает значительным пусковым моментом и не допускает «разноса». Изменяя соотношение между МДС обмоток, можно приблизить характеристику к кривой 1 или 2.