Треугольники токов и проводимостей

На рисунке построен треугольник токов, катеты которого равны активной I_a и реактивной I_P составляющим тока, а гипотенуза – полному току I. Если I_L > I_C, то I_P отстает по фазе от напряжения на угол π/2, а полный ток I – на φ (0 < φ < π/2). Если I_L < I_C , то ток I_P опережает напряжение на угол φ, а полный ток I - на (-π/2 < φ < 0).

Если каждую сторону треугольника токов разделить на напряжение, то получим треугольник проводимостей, из которого следует, что полная проводимость цепи равна корню квадратному из суммы квадратов активной G и реактивной B_Р = B_L – B_C проводимостей.

Полный ток цепи при параллельном соединении элементов:

I = YU =

Треугольник токов Треугольник проводимостей

Из треугольника проводимостей получаем соотношения:

G = Ycosφ;

B = Ysinφ;

φ = arctg(B/G) = arctg((B_L – B_C)/G).

Полная проводимость цепи в комплексной форме

Y = 1/Z = 1/(Ze ^jφ) =Ye^–jφ = G – jB,

где G и B – активная и реактивная проводимости соответственно.

Если в цепи преобладает индуктивная проводимость (В_L > В_C), то реактивная проводимость в комплексной форме отрицательна, а если преобладает емкостная проводимость (В_L < В_C), то – положительна.

Параллельное соединение нескольких электроприемников

Рассмотрим схему параллельного соединения электроприемников, обладающих активным и реактивными сопротивлениями. Как правило, подводимое к цепи напряжение и параметры параллельных ветвей заданы.

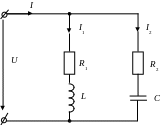
Электрическая цепь при параллельном соединении

нескольких электроприемников

Комплексный ток в ветви k можно определить по закону Ома:

İ_k = = I_ke^{- jk} = I_ka – jI_kp,

где φ_k = arctg(Х_k /R_k) - угол сдвига фаз.

Векторная диаграмма цепи при параллельном соединении нескольких элементов

Комплексные проводимости ветвей определяют следующим образом.

Полная проводимость ветви с R- L

Y₁ = 1/Z₁ = 1/(R₁+jX₁)

(R₁ - jX_L)/(R₁ + jX_L) (R₁ – jX_L) = R₁/Z₁² – jX_L/Z₁².

Откуда активная проводимость

G₁ = R₁/Z₁².

Индуктивная проводимость

B_L = – jX_L/Z².

Полная проводимость ветви с R и C

Y₂ = 1/Z₂ = 1/( R₂ – jX_C) = (R₂+JX_C)/[(R₂- jX_C)(R₂ + jX_C)] =

= R₂/Z₂² + jX_C/Z₂²

Активная проводимость второй ветви

G₂ = R₂/Z ₂².

Емкостная проводимость

B_C = + jX_C/Z₂².

Полная проводимость всей цепи при B_L > B_C,

Y= Y₁ + Y₂ = (G₁ + G₂)+ j(B_C – B_L) = Ye^-jφ,

где G₁ + G₂ = G - активная проводимость всей цепи; B_C – B_L= В_р – реактивная проводимость всей цепи, φ = arctg(В_р /G) – угол сдвига фаз.

Складывать модули полных проводимостей ветвей нельзя.

Комплексный ток цепи İ = Y _{= /} Z.

Резонанс токов

В электрической цепи при параллельном соединении ветвей с R(G), L(B_L), C(B_C) ток определяется по формуле

I = YU =

Интерес представляет случай, когда индуктивная и емкостная проводимости равны между собой. Тогда полная проводимость цепи Y = G, так как, B_L = B_C, а полный ток I = GU имеет минимальное значение и является по характеру активным. Следовательно, cosφ = 1.

Такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равно нулю, а цепь потребляет только активную мощность, называют резонансом токов.

В режиме резонанса токов токи I_L = I_C и могут превышать общий ток I в цепи в B_L/G раз, если B_L = B_C > G.

Векторная диаграмма для режима резонанса токов:

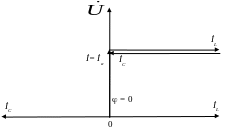
Векторная диаграмма для режима резонанса токов

Несмотря на то что в ветвях с L и C протекают токи, превышающие полный ток, эти токи всегда противоположны по фазе друг другу. Поэтому через каждую четверть периода происходит обмен энергией между магнитным полем индуктивной катушки и электрическим полем конденсатора, который поддерживается напряжением источника питания.

Режим резонанса токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты при заданных параметрах цепи. Графики зависимости тока в линии и коэффициента мощности от мощности конденсатора:

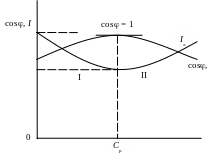
Зависимость тока в линии и коэффициента мощности от емкости

конденсаторов С; I – область недокомпенсации; II – область перекомпенсации

Резонанс токов нашел широкое применение в мероприятиях по повышению коэффициента мощности промышленных предприятий.

Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер: асинхронные двигатели, работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и др. Эти потребители работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность, что приводит к необоснованной загрузке реактивным током источников питания и линии электропередач.

Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею косинусных конденсаторов:

Электрическая цепь с параллельным включением конденсатора

Векторная диаграмма цепи:

Векторная диаграмма токов

На векторной диаграмме I - полный ток, протекающий по линии электропередач до подключения батареи косинусных конденсаторов, I_л - после подключения батареи.

Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность установки, так как

Q = Q_L – Q_C,

и тем самым увеличивает коэффициент мощности.

Повышение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих потребитель с источником питания и полной мощности источника.