5. Средние угловая скорость и ускорение

Средний вектор угловой скорости

‹ ω › = Δφ /Δ t,

где Δφ − приращение угла поворота за интервал времени Δ t .

Средний вектор углового ускорения

‹ β › = Δω /Δt ,

где Δω − приращение вектора угловой скорости за интервал времени Δ/t.

Средняя угловая скорость

‹ ω › = Δ φ /Δt ,

Среднее угловое ускорение;

‹ β › = Δω /Δt.

6. Мгновенные угловая скорость и ускорение

Мгновенная угловая скорость

ω = dφ /dt ; ωz = dφ / dt ,

где ωz − проекция угловой скорости на ось вращения.

Угловое ускорение

‹ β › = dω / dt ; βz = dωz / dt ,

где βz − проекция углового ускорения на ось вращения.

Угловая скорость и угловое ускорение являются аксиальными вектора-

ми, их направления совпадают с неподвижной в пространстве осью враще-

ния.

Связь между линейными и угловыми величинами:

S = R φ ; v = ω R ; aτ = βz R ; an = v² / R = ω² · R ,

где R − радиус окружности, по которой движется точка; S − длина дуги

окружности; φ − угол поворота, v − линейная скорость; βz − проекция уг-

лового ускорения на ось вращения; ω − угловая скорость; aτ − тангенци-

альное ускорение; аn − нормальное ускорение.

При постоянной угловой скорости ω = 2π / T, где Т − период(время од-

ного полного оборота); v − частота вращения (число оборотов, совершаемых

движущейся точкой в единицу времени) . 6

7. Кинематическое уравнение вращательного движения мате-

риальной точки

t

φ = ∫ ωz dt ,

o

где φ − угол поворота; ωz − проекция угловой скорости на ось вращения. Ес-

ли угловое ускорение β = const, то φ = φо + ωоt + βt²/ 2 , где ωо − началь-

ная угловая скорость. Угловая скорость при таком вращении

ω = ωо + βt.

8. Ускорение в плоском криволинейном движении

a = аn + aτ , a = √ an² + aτ ² , или

а = R √ β ² + ω²*² ,

где аτ = dv / dt − скорость изменения модуля скорости (см. рис. 1)

Сопоставление уравнений поступательного и

вращательного движений приведено в табл № 1.

Рис. 1 Таблица № 1

Поступательное движение	Вращательное движение
a = const	β = const
sx = x − xo = vox t + ax t² / 2	φz − φoz = ωoz t + β t² / 2
vx = vox + ax t	ωz = ωoz + βz t
2 axsx = vx² − vox²	2βz φz = ωz² − ωoz²

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Что изучает механика как один из разделов физики? Каково содержание:

а) классической (ньютоновской); б) релятивистской; в) квантовой механики?

2. Почему приходится использовать модельные представления и абстрагиро-

ванные понятия при изучении реальных физических явлений и объектов?

Дайте определения:

а) материальной точки(частицы);

б) системы материальных точек;

в) абсолютно твердого тела.

3. Каково содержание понятий пространства и времени в классической и релятиви-

стской механике? Что означает “однородность пространства”, “однородность вре-

мени”, “изотропность пространства”?

4. Какие существуют способы описания движения материальной точки? Дайте опре-

деления системы отсчета, системы координат, радиуса-вектора r .

5. Покажите, что задание кинематического закона движения в координатной форме

х = х (t), y = (t) , z = z (t) эквивалентно заданию его в векторной форме r =r (t), где

х, у,z – декартовы координаты положения материальной точки, r – её радиус –

вектор. Каковы преимущества векторного описания движения? 7

6. Дайте определение кинематических величин: а)перемещения r ; б) скорости v ;

в) ускорения a. В каких единицах измеряются эти величины? Как ориентирова-

ны векторы скорости и ускорения относительно траектории и друг друга?

7. Что называется тангенциальным и нормальным ускорением? Отчего зависит угол

между векторами скорости v и полного ускорения a движущейся материальной

точки?

8. Какие векторы называются аксиальными? Дайте определение : а) угла поворота ;

б)угловой скорости; в)углового ускорения относительно неподвижной в простран-

стве оси вращения. В каких единицах измеряются эти величины?

9. Частица движется по закону r = ( vo t − g t² / 2 ) k , где vo и g − известные пос-

тоянные; k − орт координатной оси z. Найдите скорость v частицы и её уско-

рение a , а также их проекции vz =d z / d t и аz = d vz / d t как функции времени.

10.Ускорение движущейся частицы a = A i , где А – известная постоянная; i – орт

координатной оси x. В момент времени t = 0 x = xo и vx = vo , где xo и vo - изве-

стные постоянные(начальные условия). Найдите проекцию скорости vx = d x / d t

и координату х как функцию времени.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. С башни в горизонтальном направлении брошено тело с

начальной скоростью vо = 10 м/с. Пренебрегая сопротивлением воздуха, опре-

делить для момента времени t = 2 с после начала движения:1) скорость тела v;

2) радиус кривизны R его траектории.

Д а н о: vо = 10 м/с, t = 2 с.

О п р е д е л и т ь: 1) v; 2) R.

Р е ш е н и е. Тело участвует в двух взаимно перпендикулярных движе-

ниях: равномерном прямолинейном движении вдоль оси Ох ( со скоростью vо)

и свободном падении вдоль оси Оy (со скоростью vy = gt) (рис. 2). Следова-

тельно, скорость тела в точке A

v = √ vо² + g²t²

Из рисунка видно, что нормальное ускорение тела

an = g cos α = gvо / √ vо² + g²t² .

С другой стороны, an = v²/R, откуда

R = v²/an = (vо² + g²t²)³/² /gvо.

Рис. 2 Вычисляя, получаем:

1) v= 22 м/с; 2) R = 109 м.

Пример 2.Кинематическое уравнение движения материальной точки по пря-

мой ( ось x ) имеет вид х = A + Bt + Ct³, где A = 4 м, B = 2 м /с, C = −0,5 м/с².

для момента времени t1 = 2 c определить : 1) координату x1 точки, 2) мгновен-

ную скорость v1, 3) мгновенное ускорение a1.

Д а н о: A = 4 м, B = 2 м/с, С = −0,5 м/с², t1 = 2 с.

О п р е д е л и т ь: 1) x1; 2) v1; 3) a1.

Р е ш е н и е. 1. Координату точки, для которой известно кинематическое 8

уравнение движения, найдем, подставив в уравнение движения вместо t задан-

ное значение времени t1 :

x1 = A + Bt1 + Ct³1.

Подставим в это выражение значения A, B, C, t1 и произведем вычисления:

x1 = ( 4 + 2 · 2 − 0,5 · 2³ ) м = 4 м.

2. Мгновенную скорость в произвольный момент времени найдем, про-

дифференцировав координату x по времени: v = dx/d t = B + 3Ct². Тогда в

данный момент времени t1 мгновенная скорость

v1 = B + 3Ct²1.

Подставим сюда значения B, C, t1 и произведём вычисления:

v1 = −4 м/с.

Знак минус указывает на то, что в момент времени t1 = 2 c точка движется в

отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв

вторую производную от координаты x по времени: a = d²x/dt² = dv/dt = 6Сt.

мгновенное ускорение в заданный момент времени t1 равно

a1 = 6Ct1.

Подставим значения C, t1 и произведем вычисления:

a1 = (−6 · 0.5 · 2) м/с = −6 м/с² .

Знак минус указывает на то, что направление вектора ускорения совпадает

с отрицательным направлением координатной оси, причем в условиях данной

задачи это имеет место для любого момента времени.

Пример 3. Кинематическое уравнение движения материальной точки по

прямой(ось x ) имеет вид x(t) = A + Bt + Сt², где A = 5 м, B = 4 м/с, C =−1 м/с².

1. Построить график зависимости координаты x и пути s от времени.

2. Определить среднюю скорость ‹ vx › за интервал времени от t1 = 1 c до

t2 = 6 c. 3. Найти среднюю путевую скорость ‹ v › за тот же интервал времени.

Р е ш е н и е. 1. Для построения графика зависимости координаты точки

от времени найдем характерные значения координаты – начальное и макси-

мальное и моменты времени, соответствующие указанным координатам и ко-

ординате, равной нулю.

Начальная координата соответствует моменту t = 0. Её значение равно

xo = x(0) = A = 5 м.

Максимальное значение координата достигнет в тот момент, когда точка

начинает двигаться обратно (скорость меняет знак). Этот момент времени

найдем, приравняв нулю первую производную от координаты по времени:

v = dx/dt = B + 2Ct = 0, откуда

t = −B/2C = 2 c.

9

Максимальная координата

xmax = x(2) = 9 м.

Момент времени t, когда координата x = 0, найдем из выражения

x = A + Bt + Ct² = 0.

Решим полученное квадратное уравнение относительно t :

t = ( −B ± √ B² −4AC ) / 2C .

Подставим значения A, B, C и произведём вычисления:

t = (2 ± 3) c.

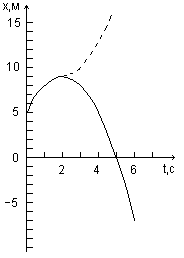Таким образом, получаем два значения времени: t′=

= 5 c и t" = −1 c. Второе значение времени отбра-

сываем, так как оно не удовлетворяет условию за-

дачи ( t≥ 0 ).

График зависимости координаты точки от вре-

мени представляет собой кривую второго порядка.

для его построения необходимо иметь пять точек,

так как уравнение кривой второго порядка содер-

жит пять коэффициентов. Поэтому кроме трех вы-

численных ранее характерных значений координа-

ты найдем ещё два значения координаты, соответ-

ствующие моментам t1 = 1 c и t2 = 6 c:

x1 = A + Bt1 + Ct²1 = 8 м, x2 = A + Bt2 + Ct²2 = −7 м.

Рис. 3

Полученные данные представим виде таблицы:

Время, с	to = 0	t1 = 1	tв = 2	t′ = 5	t2 = 6
Координата, м	xо = A = 5	x1 = 8	xmax = 9	x = 0	x2 = −7

Используя данные таблицы, чертим график зависимости координаты

от времени ( рис. 3).

График пути построим, исходя из следующих соображений: 1) путь и

координата до момента изменения знака скорости совпадают; 2) начиная

с момента возврата ( tв ) точки она движется в обратном направлении и,

следовательно, координата её убывает, а путь продолжает возрастать по

тому же закону, по которому убывает координата.

Следовательно, график пути до момента времени tв = 2 с совпадает с

10

графиком координаты, а начиная с этого момента является зеркальным

отображением графика координаты.

2. Средняя скорость ‹ vx › за интервал времени t2 − t1 определяется

выражением

‹ vx › = (x2 − x1) / (t2 − t1).

Подставим значения x1, x2, t1, t2 из таблицы и произведем вычисления

‹ vx › = ( −7 −8 ) / (6 −1) м = − 3 м/c.

3. Среднюю путевую скорость ‹ v › находим из выражения

‹ v › = s / ( t2 − t1 ),

где s − путь, пройденный точкой за интервал времени t2 − t1. Из графика

на рис. 3 видно, что этот путь складывается из двух отрезков пути: s1 =

= xmax − x1, который точка прошла за интервал времени tв − t1, и s2 =

= xmax + | x2 |, который она прошла за интервал t2 − tв. Таким образом,

путь

s = s1 +s2 = ( xmax − x1 ) + ( xmax + | x2 | ) = 2 xmax + | x2 | − x1.

Подставим в это выражение значения x1, | x2 |, xmax и произведем вычис-

ления

‹ s › = ( 2 · 9 + 7 − 8 ) м = 17 м.

Тогда искомая средняя путевая скорость

‹ v ›= 17 / ( 6 − 1 ) м/c = 3.4 м /c .

Заметим, что средняя путевая скорость всегда положительна.

Пример 4. Автомобиль движется по закруглению шоссе, имеющему ра-

диус кривизны R = 50 м. Уравнение движения автомобиля ξ (t) = A+ Bt+ Ct²,

где ξ означает криволинейую координату, отсчитанную по дуге окружности,

A = 10 м, B = 10 м/c, C =−0,5 м /c². Найти : 1) скорость v автомобиля, его

его тангенциальное aτ, нормальное an, и полное a ускорения в момент вре-

мени t = 5 c; 2) длину пути s и модуль перемещения | Δr | автомобиля за

интервал времени τ = 10 c, отсчитанный с момента начала движения.

Р е ш е н и е. 1. Зная уравнение движения, найдем скорость, взяв первую

производную от координаты по времени: v = dξ / dt = B + 2Ct. Подставим в

это выражение значения B, C, t и произведем вычисления:

v = 5 м /c.

Тангенциальное ускорение найдем, взяв первую производную от скорости

по времени: aτ = d v /dt = 2 C. Подставив значение C, получим

aτ = − 1 м/c².

11

Нормальное ускорение определяется по формуле an = v²/R. Подставим сюда

найденное значение скорости и заданнон значение радиуса кривизны траекто-

рии и произведем вычисления:

an = 0,5 м/c².

Полное ускорение, как видно из рис.1, является геометрической суммой

ускорений aτ и an: a = aτ + an. Модуль ускорения a = √ a²τ + a²n . Подста-

вив в это выражение найденные значения aτ и an, получим

a = 1.12 м/c².

3. Чтобы определить путь s, пройденный автомобилем, заметим, что в слу-

чае движения в одном направлении (как это имеет место в условиях данной за-

дачи ) длина пути s равна изменению криволинейной координаты ξ , т.е.

s = ξ ( τ ) − ξ ( 0 ), или s = A + Bτ + Cτ² − A = B + C τ² .

Подставим в полученное выражение значения B, C, τ и произведем вычисле-

ния:

s = 50 м.

Модуль перемещения, как это видно из рис.4, равен

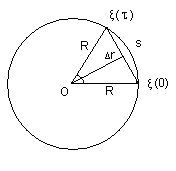
|Δr| = 2 R sin ( α /2 ),

где α − угол между радиусами-векторами, определя-

ющими начальное ξ (0) и конечное ξ (τ) положения

автомашины на траектории. Этот угол (в радианах) на-

ходим как отношение длины пути к радиусу кривизны R

траектории, т.е. α = s / R. Таким образом,

Рис.4 |Δr| = 2 R sin (s / R).

Подставим сюда значения R, s и произведем вычисления:

|Δr| = 47.5 м.

Пример 5. Диск радиусом R = 5 см вращается вокруг неподвижной

оси так, что зависимость угловой скорости от времени задается уравнением

ω = 2At + 5Bt²*² ( A = 2 рад / c², B = 1 рад / c² c³ ). Определить для точек на

ободе диска к концу первой секунды после начала движения: 1) полное уско-

рение; 2) число оборотов N, сделанных диском.

Д а н о: R = 5 см = 0.05 м, ω =2At + 5Bt²*,² A = 2 рад / c² ; B = 1 рад /c²c³,

t = 1 c.

О п р е д е л и т ь: 1) a; 2) N.

Р е ш е н и е. Полное ускорение a = √ aτ² +an² , где тангенциальная состав-

12

ляющая ускорения aτ = βR ( β = dω / dt − угловое ускорение ), а нормальная

составляющая ускорения an = ω²R.

По условию задачи, ω = 2At + 5Bt²*²; следовательно,

aτ = βR = R dω /dt = R ( 2A + 5B t³ ),

an = ω²R = R ( 2At + 5Bt²*²)²,

откуда полное ускорение

a = R √ (2At + 20Bt³)² + (2At + 5Bt²*²)²*².

Угол поворота диска φ = 2π N ( N − число оборотов), но угловая ско-

рость ω = dφ / dt ; следовательно,

t t

φ = ∫ ωdt = ∫ (2At + 5Bt²*²)dt = At²+ Bt²t³.

о o

Тогда число оборотов, сделанных диском,

N = φ / (2π) = ( At² + Bt²*³ ) / 2π .

Вычисляя, получим: 1) a = 4.22 м/c²ж; 2) N = 0.477.

Пример 6. Маховик, вращавшийся с постоянной частотой no = 10 c־¹,

при торможении начал вращаться равнозамедленно. Когда торможение пре-

кратилось, вращение маховика снова стало равномерным, но уже с частотой

n = 6 c־¹. Определить угловое ускорение β маховика и продолжительность

t торможения, если за время движения маховик сделал N оборотов.

Р е ш е н и е. Угловое ускорение маховика связано с начальной ωо и ко-

нечной ω угловыми скоростями соотношением ω² − ωo² = 2βφ, откуда

откуда β = ( ω² − ωo² ) / (2φ). Но так как φ = 2π N, ω = 2 π N, то

β = ( ω² − ωo² ) / 2φ = π ( n² − no² ) / N .

Подставив значения π, n, no, N и вычислив, получим

β = 3.14 ( 6² − 10² ) / 50 рад / с² = −4.02 рад / c².

Знак минус указывает на то, что маховик вращается замедленно.

Определим продолжительность торможения, используя формулу,связыва-

ющую угол поворота φ со средней угловой скоростью ‹ ω › вращения и

и временем t: φ = ‹ ω › t. По условиям задачи, угловая скорость линейно

зависит от времени и поэтому можно написать ‹ ω › = ( ωo + ω ) / 2 , тогда

φ = ( ωo + ω ) t / 2 = π ( no + n ) t ,

откуда

t = φ / π ( no + n ) = 2 N / (no + n ).

13

Подставив числовые значения и произведя вычисления, получим

t = 2 · 50 / ( 10 + 6 ) = 6.25 с.

ЗАДАЧИ ГРУППЫ А

1.(В.1.23) Зависимость пройденного телом пути s от времени t да-

ется уравнением s =А - Вt + Ct², где А = 6 м, В = 3 м/с и С = 2 м/c². Найти

среднюю скорость <v> и ускорение a тела для интервала времени 1 ≤ t ≤ 4.

Построить график зависимости пути s, скорости v и ускорения a от време-

ни t для интервала 0 ≤ t ≤ 5 c через 1 с.

Ответ: <v> = 7 м/c; a = 4 м/c² .

2.(В.1.26) С башни высотой h = 25,0 м горизонтально брошен камень

со скоростью vx = 15 м/c. Какое время t камень будет в движении? На ка-

ком расстоянии l от основания башни он упадет на землю? С какой скоро-

стью v он упадет на землю? Какой угол φ составит траектория камня с го-

ризонтом в точке его падения на землю?

Ответ : t = 2,3 c; l = 34 м; φ = 56°.

3.(В.1.31) Камень брошен горизонтально со скоростью vx = 10,00 м/с.

Найти радиус кривизны R траектории камня через время t = 3.00 с пос-

ле начала движения.

Ответ : R = 305 м.

4.(В.1.32) Мяч брошен соскоростью vо = 10.00 м/с под углом α = 40º

к горизонту. На какую высоту h поднимется мяч? На каком расстоянии l

от места бросания он упадет на землю? Какое время t он будет в движе-

нии?

Ответ : h = 2.1 м; l = 10.0 м; t = 1.3 с.

5.(В.1.34) Тело брошено со скоростью vо под углом к горизонту. Вре-

мя полета t = 2.2 c. На какую высоту h поднимется тело ?

Ответ: h = 5.9 м.

6.(В.1.36) Тело брошено со скоростью vо = 14.7 м/с под углом α = 30º

к горизонту. Найти нормальное a n и тангенциальное a τ ускорения тела

через время t = 1.25 с после начала движения.

Ответ: a n = 9.2 м/c²; a τ = 3.5 м/с².

7.(В.1.37) Тело брошено со скоростью vо = 10.0 м/с под углом α = 45º

к горизонту. Найти радиус кривизны R траектории движения тела через

время t = 1.00 с после начала движения.

Ответ: R = 6.3 м.

8.(В.1.39) С башни высотой hо = 25.0 м брошен камень со скоростью

vo = 15 м/с под углом α = 30º к горизонту. Какое время t камень будет в дви-

жении? На каком расстоянии l от основания башни он упадет на землю? С ка-

14

кой скоростью v он упадет на землю? Какой угол φ составит траектория дви-

женияния с горизонтом в точке его падения на землю?

Ответ: t = 3.16 с; l = 41.1 м ; φ = 61º.

9.(В.1.50) Вал вращается с частотой n =180 об/мин. С некоторого момен-

та вал начал вращаться равнозамедленно с угловым ускорением β = 3 рад/с².

Через какое время t вал остановится? Найти число оборотов N вала до оста-

новки.

Ответ: t = 6.3 с ; N = 9.4 об.

10.(В.1.53) Точка движется по окружности радиусом R = 10.0 см с посто-

янным тангенциальным ускорением a τ. Найти нормальное ускорение a n точ-

ки через время t = 20.0 с после начала движения, если известно, что к концу

пятого оборота после начала движения линейная скорость точки v = 10.0

см /c.

Ответ: a n = v v³ t²/16π²N²R³ = 0.010 м/с².

11.(В.1.55) Колесо радиусом R = 10 см вращается с угловым ускорением

β = 3.14 рад/с² . Найти для точек на ободе колеса к концу первой секунды пос=

ле начала движения: а) угловую скорость ω ; б) линейную скорость v ; в) тан-

генциальное ускорение aτ ; г) нормальное ускорение n ; д) полное ускорение a;

е) угол φ, составляемый вектором полного ускорения с радиусом колеса.

Ответ: ω = 3.14 рад/с ; v = 0.314 м/с ; aτ = 0.314 м/с² ; a n = 0.986 м/с²;

a = 1.03 м/с² ; φ = 17º46′ .

12.(1.59) Колесо вращается с угловым ускоренрем β = 2.00 рад/с². Че-

рез время t = 0.500 c после начала движения полное ускорение колеса а = 13.6

см/с². Найти радиус R колеса.

Ответ: R = a/β√ (1 + β²t²* ² ) = 6.1 см.

13.(В.1.61) Колесо радиусом R = 5.00 см вращается так, что зависимость

угла поворота радиуса колеса от времени дается уравнением φ = A + Bt + Ct² +

+ Dt³, где D = 1.000 рад/с³. Для точек, лежащих на ободе колеса, найти прира-

щение модуля тангенциального ускорения Δaτ за единицу времени.

Ответ: Δaτ = 0.3 м/с².

14.(В.1.64) Во сколько раз нормальное ускорение an точки, лежащей на

ободе вращающегося колеса, больше ее тангенциального ускорения aτ для того

момента, когда вектор полного ускорения точки составляет угол φ = 30° с век-

тором её линейной скорости?

Ответ: an /aτ = tg φ = 0.58.

ЗАДАЧИ ГРУППЫ Б

1.( Ч.1.4) Первую половину пути тело двигалось со скоростью v1 = 2 м /c,

вторую − со скоростью v2 = 8 м /c. Определить среднюю путевую скорость ‹ v ›.

15

Ответ: ‹ v › = 2v1·v2 / ( v1 + v2 ) = 3,2 м/c .

2.( Ч.1.5) Тело прошло первую половину пути за время t1 = 2 c, вторую-за

время t2 = 8 м /c. Определить среднюю путевую скорость ‹ v › тела, если дли-

на пути s = 20 м.

Ответ: ‹ v › = s / ( t1 + t2 ) = 2 м /c.

3.(И.1.6.) Корабль движется по экватору на восток со скоростью vo =30

км /ч. С юго-востока под углом φ = 60º к экватору дует ветер со скоростью v =

= 15 км / ч. Найти скорость v' ветра относительно корабля и угол φ' между эква-

тором и направлением ветра в системе отсчета, связанной с кораблем.

Ответ: v' = √ ( vo² + v² + 2 vo v cos φ ) ≈ 40 км / ч, φ' = 19º.

4.(Ч.1.26) Материальная точка движется в плоскости согласно уравнению

r (t) = A t³ i + B t² j. Написать зависимости : 1) v (t), 2) a (t).

Ответ : 1) v (t) = 3A t²i + 2B t j ; 2) a (t) = 6 At i + 2B j.

5.(Ч.1.33) Движение точки по окружности радиусом R = 4 м задано уравне-

нием ξ = А + В t + C t² , где ξ − криволинейная координата, отсчитанная по

дуге окружности, А = 10 м, В = − 2 м /c, C = 1 м/c². Найти тангенциальное аτ,

нормальное аn и полное а ускорения точки в момент времени t = 2c.

Ответ : 2 м /c² ; 1 м /c² ; 2.24 м /c² .

6.(Ч.1.36) Движение точки по кривой задано уравнениями х = А1 t³ и у =А2t,

где А1 = 1 м /c³, А2 = 2 м/c. Найти уравнение траектории точки, её скорость v и

полное ускорение а в момент времени t = 0.8 c.

Ответ : у³ − 8х ; 2.77 м /c ; 4.8 м/c².

7.(Ч.1.59) Диск вращается с угловым ускорением β = − 2 рад /c². Сколько

оборотов N сделает диск при изменении частоты вращения от n1 = 240 мин ־¹

до n = 90 мин ־¹ ? Найти время Δ t, в течение которого это произойдет.

Ответ : N = π ( n2² − n1² ) / β = 21.6; Δ t = 2 π ( n2 − n1 ) / β = 7.85 c.

8. На вал радиусом R = 10 см намотана нить, к концу которой призана гиря.

двигаясь равноускоренно, гиря за t = 20 с от начала движения опустилась на h =

= 2 м. Найти угловую скорость и угловое ускорение вала для этого момента вре-

мени.

Ответ : ω = 2 h /(Rt) = 2 рад /c; β = 2h /(Rt ²) = 0.1 рад /c.

9.(Ч.1.49) Тело брошено под углом φ = 30º к горизонту. Найти тангенци-

альное аτ и нормальное аn ускорения в начальный момент времени движения.

Ответ : 4.9 м /c² ; 8.49 м /c² .

10. Тело брошено со скоростью vo = 20 м /c под углом φ = 30º к горизонту.

пренебрегая сопротивлением воздуха, найти скорость v тела, а также его нор-

мальное аn и тангенциальное аτ ускорения через t = 1.5 c после начала движе-

ния. На какое расстояние х переместится за это время тело по горизонтали и на

какой высоте у оно окажется?

Ответ : v = 17.9 м /c; a n = 9.72 м /c²; aτ = 2.67 м /c² ; x = 26 м; y = 4м.

16

11.(C.1.15) Частица движется равномерно по часовой стрелке по окруж-

Ности радиуса R , делая за время τ один оборот. Окружность лежит в коор-

динатной плоскости х,у, причем центр окружности совпадает с началом коор-

динат. В момент t = 0 частица находится в точке с координатами х = 0, у = R.

Найти среднее значение скорости точки за промежуток времени: а) от 0 до

τ /4, б) от 0 до τ /2, в) от 0 до 3τ /4, г) от 0 до τ, д) от τ /4 до 3 τ /4.

Ответ: a)‹v › = (4 /τ) R ( i − j ), б)‹ v › = − (4 /τ) R j, в)‹ v ›=−(4/3)R(i + j),

г) ‹ v › = 0, д) ‹ v › = −( 4/τ)R i.

12.(C.1.29) Точка движется вдоль оси х , причем координата х изменя-

ется по закону х = A cos (2π /T) t. Найти : a) выражения для проекций на ось

х скорости v и ускорения а точки, б) путь s1, пройденный точкой за про-

межуток времени от t =0 до t = T/8, в) путь s2, пройденный точкой за проме-

жуток времени от t = T/8 до t = T/4, г) путь s , пройденный точкой за проме-

жуток от 0 до t = T.

Ответ : а) vx = − ( 2π / T) A sin ( 2π /T) t, ax =−( 2π /T)² A cos ( 2π /T) t,

б) s1 = 0.293A, в) s2 = 0,707 A, s = 4A .

ЗАДАЧИ ГРУППЫ С

1.(И.1.13) Точка А движется равномерно со скоростью v так, что

Вектор v все время “ нацелен “ на точку В, которая в свою очередь дви-

жется прямолинейно и равномерно со скоростью u < v. В начальный момент

v перпендикулярен u и расстояние между точками равно l. Через сколько

времени τ точки встретятся?

Ответ: τ = v l / ( v² - u² ).

2.(И.1.20) Радиус-вектор частицы меяется со временем по закону r =

= b t( 1- α t ), где b − постоянный вектор, α − положительная постоянная. Най-

ти: a) скорость v и ускорение а частицы в зависимости от времени;

б) промежуток времени Δ t, по истечении которого частица вернется в ис-

ходную точку, а также путь s, который она пройдет при этом.

Ответ : a) v = b (1 – 2 α t), a = − 2 αb = const; Δt = 1/α , s = b/2α.

3.(И.1.21) В момент t = 0 частица вышла из начала координат в поло-

жительном направлении оси х. Её скорость меняется со временем по закону

v = vo ( 1 – t/τ ), где vo − начальная скорость, модуль которой vo = 10,0 cм/c,

τ = 5.0 c. Найти: а) координату х частицы в моменты времени 6,0, 10 и 20 с;

б) моменты времени, когда частица будет находться на расстоянии 10.0 см от

начала координат.

Ответ : a) x = vo t ( 1 – t /2τ); 0.24, 0 и −2.0 м; б) 1.1, 9 и 11 с.

4.(И.1.24) Радиус-вектор точки А относительно начала координат меня-

ется со временем t по закону r = α t i + β t² j , где α и β − постоянные,

i и j − орты осей х и у. Найти: a) уравнение траектории точки у ( х );

изобразить её график; б) зависимости от времени скорости v, ускорения а

и модулей этих величин; в) зависимость от времени угла φ между вектора-

ми а и v.

17

Ответ: а) y = x² β / α²;

б) v = α i + 2β t j , a = 2 β j , v = √ α² + 4β²t² , α = 2β ;

в) tg φ = α /2β t.

5.(Т.1.25) Нормальное ускорение точки, движущейся по окружности ради-

усом R = 4 м, задается уравнением аn = A + В t + C t² ( A = 1 м /c², B = 6 м/c³,

C = 9 м /c²*². Определить: 1) тангенциальное ускорение аτ точки; 2) путь s,

пройденный точкой за время t1 = 5 c с после начала движения; 3) полное уско-

рение а для момента времени t2 = 1 c.

Ответ: aτ = 6 м /c²; s = 85 м; a = 6.32 м /с².

6.(Т.1.28) Точка движется в плоскости ху из положения с координатами

х = у = 0 со скоростью v = a i + bx j , где а и b − постоянные; i, j − орты

осей х и у . Определить: 1) уравнение траектории точки у (х) ; 2) форму

траектории.

Ответ: 1) у = bx² / 2a ; 2) парабола.

7.(И.1.10) Два тела бросили одновременно из одной точки: одно − верти-

кально вверх, другое − под углом φ = 60º к горизонту. Начальная скорость

каждого тела vo = 25 м /c. Пренебрегая сопротивлением воздуха, найти рассто-

яние l между телами через t =1.7 c.

Ответ: l = vo t √ 2(1 – sin φ ) = 22 м.

8.(С.1.32) Небольшое тело (материальная точка) брошено из точки О под

углом α к горизонту с начальной скоростью vo ( рис. 5). Пренебрегая сопро-

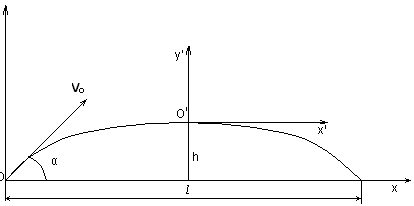тивлением воздуха, найти:

а) время полета τ,

б) дальность полета l,

в) наибольшую высоту поднятия тела h,

г) уравнение траектории тела в координатах

х', у',

д) значения | dv /dt | и d | v | /dt в вершине

траектории,

Рис.5 е) радиус кривизны R траектории в точках

О и О'.

Точки бросания и падения считать лежащими на одном уровне.

Ответ: a) τ = 2 vosin α / g , б) l = vo² sin 2α / g , в) h = vo² sin²α / 2g,

г) у' = − g x' ²/ 2 vo² cos² α , д) | dv /dt | = g, d | v| /dt = 0, е) Ro = vo² / g cos α ,

R o' = vo² cos²α /g .

9.(И.1.46) Твердое тело вращается вокруг неподвижной оси по закону

φ = a t − b t³,

где a = 6.0 рад /с , b = 2.0 рад/c. Найти: средние значения угловой скорости

и углового ускорения за промежуток времени от t = 0 до остановки; б) угловое

ускорение в момент остановки.

Ответ: a) ‹ ω › = 2a /3 = 4 рад /c , ‹ β › = √ 3 ab = 6 рад /c²;

Б) β = 2 √ 3 аb = 12 рад /c².

18

10.(И.1.47) Твердое тело начинает вращаться вокруг неподвижной оси с

угловым ускорением β = αt, где α = 2.0 * 10־² рад /c³. Через сколько времени

после начала вращения вектор полного ускорения произвольной точки тела бу-

дет составлять угол φ = 60º с её вектором скорости ?

Ответ: τ = ³√ (4/α) tgφ = 7 c.

11.(И.1.35) Частица движется в плоскости ху со скоростью v = αi +βxj,

где i и j − орты осей х и у , α и β − постоянные. В начальный момент

частица находилась в точке х = у = 0.

Найти:

а) уравнение траектории частицы у( х );

б) радиус кривизны R траектории в зависимости от х.

Ответ: а) х = (β /2α) x², б) R = v²/ an = v²/√ a² − aτ² = ( α / β)[1 + (xβ/α)²]³/².

12.(И.1.37) Точка движется по окружности со скоростью v = αt, где α =

= 0.50 м/c². Найти её полное ускорение а в момент, когда она пройдет n =0.10

длины окружности после начала движения.

Ответ: a = α √ 1 + (4π n)² = 0.8 м/c².

13.(И.1.41) Точка движется по плоскости так, что её тангенциальное ус-

корение аτ = α , а нормальное ускорение аn =βt²*², где α и β − положитель-

ные постоянные, t − время. В момент t = 0 точка покоилась. Найти зависи-

мости от пройденного пути s радиуса кривизны R траектории токи и её

полного ускорения а.

Ответ: R = α³ /2βs , a = α √ 1 + (4βs²/α³)² .

14.(И.1.44) Колесо вращается вокруг неподвижной оси так, что угол φ

его поворота зависит от времени как φ = βt², где β = 0.20 рад /c². Найти

полное ускорение а точки А на ободе колеса в момент времени t = 2.5 с,

если скорость точки А в этот момент v = 0.65 м/c.

Ответ: a = (v/ t) √ 1 + 4β²t²*² = 0.7 м/c².

15.(И.1.49) Твердое тело вращается вокруг неподвижной оси так, что

его угловая скорость зависит от угла φ по закону ω = ωо − а φ, где ωо и а

− положительные постоянные. В момент времени t = 0 угол φ =0. Найти

зависимости от времени:

a) угла поворота; б) угловой скорости.

- at -at

Ответ: a) φ = (1 - e ) ωo/a; ω = ωo e .

Занятие 2. Динамика прямолинейного и криволинейного

движения материальной точки

СОДЕРЖАНИЕ ТЕОРИИ

1. Дифференциальное уравнение движения материальной точки.

2. Потенциальные и диссипативные силы в механике.

3. Динамика кругового движения материальной точки.

4. Закон изменения и сохранения импульса материальной точки.

19

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ