
- •1.Случ-й экспер-т. Пространство элементар-х исходов. Дискретные и непрерывные пространства элементар-х исходов. Примеры.
- •2.Случа-е события. Пр-ы. Достоверное, невозможное, противоположное соб-я. Несовместные соб-я. Полная группа соб-й. Пр-ы.
- •3.Случ-е соб-я. Пр-ы. Операции над соб-ми.
- •3 Аксиомы а.Н. Колмогорова
- •5.Классический метод выч-ия вер-ей. Пр-ы.
- •6.Статисти-ий метод вычисления вер-ей. Пр-ы.
- •7.Элементы комбинаторики. Классификация выборок. Пр-ы. Количество перестановок.
- •9.Элементы комби-ки. Неупор-ые выборки. Пр-ы.
- •10.Теор-а сложения вер-ей для 2-х соб-й (общий и частный случаи). Те-а сложения вер-ей для 3-х событий (общий и частный случаи).
- •2)Общий случай для 3-х событий
- •14.Формула полной вероят-и. Формула Байеса.
- •15.Испытания Бернулли. Фор-а Бернулли. Наиболее вероя-е число успехов в фор-е Бернулли.
- •16.Испытания Бернулли. Формула Пуассона.
- •17.Испытания Бернулли. Локальная формула Муавра-Лапласа.
- •18.Испытания Бернулли. Интегральная формула Муавра-Лапласа.
- •19.Случайная величина. Примеры. Дискретные и непрерывные случайные величины.
- •20.Дискретная случ-я величина. Пр-ы. Закон распределения дискретной случ-й величины.
- •21.Непрерывная св Пр-ы. Закон распределения непрерывной св.
- •22.Непрерывная св. Пр-ы. Функция распределения непрерывной св и ее свойства.
- •23.Непрерывная св Пр-ы. Функция плотности непрерывной св и ее свойства.
- •24.Числовые характеристики св Математическое ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана дискретной св.
- •25.Числовые характеристики св. Математич-е ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана непрерывной св
- •26.Числовые характеристики св. Свойства математического ожидания и дисперсии.
- •27.Биномиальный закон распределения. Примеры.
- •28.Закон распределения Пуассона. Примеры. Простейший поток событий.
- •30.Показательный (экспоненциальный) закон распределения. Примеры.
- •31.Нормальный закон распределения. Пр-ы.
- •32.Вычисление вер-и попадания непрерывной св в заданный интервал с помощью функции плотности и функции распределения.
- •34.Предмет и задачи математи-ой статистики. Генеральная и выборочная совокупности.
- •35.Вариационный ряд. Статист-й закон распр-я дискретной св. Столбцовая диаграмма.
- •36.Вариационный ряд. Статистический закон распределения непрерывной св Гистограмма.
- •37.Эмпирическая функция распределения и ее график. Св-ва.
- •38.Точечные оценки числовых характеристик cв. Пр-ы. Свойства оценок: несмещенность, эффективность и состоятельность.
- •39.Точечные оценки числовых характеристик св. Оценки математ-го ожидания, дисперсии, среднего квадратического отклонения. Пр-ы.
- •40.Точечные оценки числовых характеристик св. Оценки среднего квадратического отклонения, медианы, моды (для дискретной и непрерывной случайной величины). Примеры.
- •42.Статис-ая проверка гипотез. Параметрические и непараметрические гипотезы. Вер-ти ошибок 1-го и 2-го родов. Пр-ы.
- •48.Применение метода наименьших квадратов для нахождения оценок параметров уравнения регрессии. Нелинейная регрессионная модель.
- •49.Оценка коэффициента корреляции. Св-ва.
- •50.Проверка значимости кк.
- •51. Коэффициент детерминации и его свойства.
- •52.Проверка значимости кд.
20.Дискретная случ-я величина. Пр-ы. Закон распределения дискретной случ-й величины.
Дискретной на-я СВ Х, кот-я в результате экспе-та Е может принимать только опре-ые изолированые друг от друга значения. Множество возможных значений дискр-х СВ яв-я конечным или счетным множеством. П-ы : число студентов в группе, успешно сдавших экзамен по мат-ке; число клиентов банка, своевременно возвративших кредит; число звонков, поступивших в службу такси в течение часа, и т.д. Для диск. СВ Х закон задается в виде:1) ряда распределения-таблица в 1-й строке кот-й выписаны значения СВ, а во 2-й соотве-е им вер-ти
2)функцией распределения F(х)
Fξ(x)=P{ξ<x}, x€R
Св-ва:а)облость опред-я Fξ(x)(-∞; ∞)
б)облость значения 0≤ Fξ(x)≤1
в) Fξ(x)- неубывающая
г) Fξ(x)-непрерывная
д) F(∞)= $
F(-∞)=
$
F(-∞)=
3)многоугольная
4) в виде формулы(ечсли она подчин-я ей)
21.Непрерывная св Пр-ы. Закон распределения непрерывной св.
СВ наз-я непрерывной если ее функция распределения яв-я непрерывной.. Множество возможных значений непрерывных СВ яв-я несчетным множеством. Пр-ы: время безотказной работы оборудования после очередного ремонта; время простоя клиента магазина в очереди; масса израсходованного автомобилем бензина на одном и том же расстоянии.
Закон распе-я непр-й СВ можно задать с помощью функ-и распр-я. Функ-и распр-я. яв-я функ-й распр-я. непре-й СВ если ее можно передать след образ:
F(x)= ,x€R
f(t)-
фун-я плотности.
,x€R
f(t)-
фун-я плотности.
f(x)=F(x)
Cв-ва f(x): 1) f(x)- не отрицательная (f(x)≥0)
2)

22.Непрерывная св. Пр-ы. Функция распределения непрерывной св и ее свойства.
СВ наз-я непрерывной если ее функция распределения яв-я непрерывной.. Множество возможных значений непрерывных СВ яв-я несчетным множеством. Пр-ы: время безотказной работы оборудования после очередного ремонта; время простоя клиента магазина в очереди; масса израсходованного автомобилем бензина на одном и том же расстоянии.
Закон распе-я непр-й СВ можно задать с помощью функ-и распр-я. Функ-и распр-я. яв-я функ-й распр-я. непре-й СВ если ее можно передать след образ:
F(x)= ,x€R f(t)- фун-я плотности.
23.Непрерывная св Пр-ы. Функция плотности непрерывной св и ее свойства.
СВ наз-я непрерывной если ее функция распределения яв-я непрерывной.. Множество возможных значений непрерывных СВ яв-я несчетным множеством. Пр-ы: время безотказной работы оборудования после очередного ремонта; время простоя клиента магазина в очереди; масса израсходованного автомобилем бензина на одном и том же расстоянии.
Зная фун-ю рапре-я можно найти фун-ю плотности f(x)=F(x)
Cв-ва f(x): 1) f(x)- не отрицательная (f(x)≥0)
2)
Теорема: если нек-я ξфун-я f(x) удовлет-т св-м 1и2, то сущ-т СВ(непре-я) для кот-й эта фун-я будет явл-я фун-й плотности.
24.Числовые характеристики св Математическое ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана дискретной св.
Числовые характеристики СВ
1)Математическое
ожидание-это
среднее(среднее взвешенное по вер-ти)
значение СВ. M[ξ]= =xipi+x2+p2+…
при условии, что ряд сходится абсолютно.
=xipi+x2+p2+…
при условии, что ряд сходится абсолютно.
Св-ва: 1)M[const]=const$
2)M[ξ+const]=M[ξ}+const; M[C+ξ]=CM[ξ],c=const
3) M[ξ}линейной комбинацииξ и ή есть линейная комбинация M[ξ}
M[άξ+βή]=άM[ξ]+βM[ή], ά=const, β=const
4) M[ξ}произведения 2-х СВ ξ и ή= произве-ю M[ξ} этих СВ M[ξή]=M[ξ]*M[ή]
2)мода-наибольшее веро-е значение,т.е. то значение ко-е принимается с наибо-й вер-ю.(точка локального мах функ-и плотности.(может иметь 1, 2 и более мод)
3)медиана- такое значение СВ Xmed для кот-го выполняется равенство
P{ξ< Xmed}= P{ξ> Xmed}=0,5.
Геоме-й смысл Xmed -координата той точки на оси абсцисс, для ко-й площади фигур, ограниченных кривой f(x) и осью абсцисс, одинаковы и равны ½.
4)дисперсия- мера рассеивания значений СВ относительно матем-го ожидания
D[ξ]=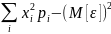
Cв-ва:1) D[ξ]≥0
2) D[ξ]=0, ξ=const
3) D[c*ξ]=c2 D[ξ]
4) D[άξ±βή]=ά2 D[ξ]+β2 D[ή], ξ и ή-независимые
5)Средне
квадратиче-ое отклонение σ[ξ]=
6)коэффициент
асимметрии показывает
на сколько распредел-е симметрично
относительно мат-го ожидания. A[X]=
7)коэф-т эксцесса
показывает
островершинность распределения.
Ex[x]= -3
-3
