- •1.Случ-й экспер-т. Пространство элементар-х исходов. Дискретные и непрерывные пространства элементар-х исходов. Примеры.
- •2.Случа-е события. Пр-ы. Достоверное, невозможное, противоположное соб-я. Несовместные соб-я. Полная группа соб-й. Пр-ы.
- •3.Случ-е соб-я. Пр-ы. Операции над соб-ми.
- •3 Аксиомы а.Н. Колмогорова
- •5.Классический метод выч-ия вер-ей. Пр-ы.
- •6.Статисти-ий метод вычисления вер-ей. Пр-ы.
- •7.Элементы комбинаторики. Классификация выборок. Пр-ы. Количество перестановок.
- •9.Элементы комби-ки. Неупор-ые выборки. Пр-ы.
- •10.Теор-а сложения вер-ей для 2-х соб-й (общий и частный случаи). Те-а сложения вер-ей для 3-х событий (общий и частный случаи).
- •2)Общий случай для 3-х событий
- •14.Формула полной вероят-и. Формула Байеса.
- •15.Испытания Бернулли. Фор-а Бернулли. Наиболее вероя-е число успехов в фор-е Бернулли.
- •16.Испытания Бернулли. Формула Пуассона.
- •17.Испытания Бернулли. Локальная формула Муавра-Лапласа.
- •18.Испытания Бернулли. Интегральная формула Муавра-Лапласа.
- •19.Случайная величина. Примеры. Дискретные и непрерывные случайные величины.
- •20.Дискретная случ-я величина. Пр-ы. Закон распределения дискретной случ-й величины.
- •21.Непрерывная св Пр-ы. Закон распределения непрерывной св.
- •22.Непрерывная св. Пр-ы. Функция распределения непрерывной св и ее свойства.
- •23.Непрерывная св Пр-ы. Функция плотности непрерывной св и ее свойства.
- •24.Числовые характеристики св Математическое ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана дискретной св.
- •25.Числовые характеристики св. Математич-е ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана непрерывной св
- •26.Числовые характеристики св. Свойства математического ожидания и дисперсии.
- •27.Биномиальный закон распределения. Примеры.
- •28.Закон распределения Пуассона. Примеры. Простейший поток событий.
- •30.Показательный (экспоненциальный) закон распределения. Примеры.
- •31.Нормальный закон распределения. Пр-ы.
- •32.Вычисление вер-и попадания непрерывной св в заданный интервал с помощью функции плотности и функции распределения.
- •34.Предмет и задачи математи-ой статистики. Генеральная и выборочная совокупности.
- •35.Вариационный ряд. Статист-й закон распр-я дискретной св. Столбцовая диаграмма.
- •36.Вариационный ряд. Статистический закон распределения непрерывной св Гистограмма.
- •37.Эмпирическая функция распределения и ее график. Св-ва.
- •38.Точечные оценки числовых характеристик cв. Пр-ы. Свойства оценок: несмещенность, эффективность и состоятельность.
- •39.Точечные оценки числовых характеристик св. Оценки математ-го ожидания, дисперсии, среднего квадратического отклонения. Пр-ы.
- •40.Точечные оценки числовых характеристик св. Оценки среднего квадратического отклонения, медианы, моды (для дискретной и непрерывной случайной величины). Примеры.
- •42.Статис-ая проверка гипотез. Параметрические и непараметрические гипотезы. Вер-ти ошибок 1-го и 2-го родов. Пр-ы.
- •48.Применение метода наименьших квадратов для нахождения оценок параметров уравнения регрессии. Нелинейная регрессионная модель.
- •49.Оценка коэффициента корреляции. Св-ва.
- •50.Проверка значимости кк.
- •51. Коэффициент детерминации и его свойства.
- •52.Проверка значимости кд.
1.Случ-й экспер-т. Пространство элементар-х исходов. Дискретные и непрерывные пространства элементар-х исходов. Примеры.
C Э- экпе-т исход ко-го нельзя заранее предсказать. Пространство элем. исходов- множество всех возможных исходов Е. Элем-е исходы, кот-е принадлежат множеству А (то есть wi €А), наз-я благоприятными событию A.
Пространство элем-х исходов, состоящее из конечного или счетного числа элементов наз-я дискретным. Пространство элем-х исходов, состоящее из несчетного числа элем-х исходов наз-я непрерывным. П-р:Е:подбр-ие прав-х монет; Е:подбр-ие игральной кости; Е:исслед-е времени безраб-й работы моб. тел.
2.Случа-е события. Пр-ы. Достоверное, невозможное, противоположное соб-я. Несовместные соб-я. Полная группа соб-й. Пр-ы.
Случайное соб-е- любое подмножество пространства элем-х соб-й. (А,В,С). П-р:
Е: под-я игр. кости;
Ω={1,..,6};А={выпадение четного числа
очков}; А={2,4,6}; Достоверным
соб-м- если
ему благоприятствует любой из элементарных
исходов(A =
).Невозможным
соб-м -если
ему не благоприятствует ни один
исход.().
Противоположным событию A
на-я соб-е
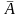 ,
состоящее в
не наступлении соб-я A.
Соб-я A
и B
на-я несовм-ми,
если они не могут произойти одновр-о,
то есть одновр-ое осуществление соб-й
A
и B
есть соб-е невозможное. Несколько
соб-й наз-я
несовм-ми,
если появление одного из них исключает
появление других в этом испыт-и.
,
состоящее в
не наступлении соб-я A.
Соб-я A
и B
на-я несовм-ми,
если они не могут произойти одновр-о,
то есть одновр-ое осуществление соб-й
A
и B
есть соб-е невозможное. Несколько
соб-й наз-я
несовм-ми,
если появление одного из них исключает
появление других в этом испыт-и.
Соб-я A и B на-я совместными, если они могут произойти одновременно. Несколько соб-й на-я совместными, если появление одного из них не исключает появление других в этом испытании.
Несколько несовмест-х соб-й образуют полную группу если в результате испыт-й обязательно появится одно из них.(А+В+..+Е=)
3.Случ-е соб-я. Пр-ы. Операции над соб-ми.
Случайное соб-е- любое подмножество пространства элем-х соб-й. (А,В,С). П-р:
Е: под-я игр. кости; Ω={1,..,6};А={выпадение четного числа очков}; А={2,4,6}; Операции:
1) Суммой(объединением)соб-й A и B (A B A + B)-состоящее в осуществлении хотя бы одного из соб-й A или B,т. е.,или A, или B, или оба вместе.
2) Произведением(пересечением)соб-й A и B (A B AB) -состоящее в одновременном осуществ-ии соб-й A и B.
3) Разностью соб-й A и B (A \ B, A – B)-состоящее в осуществ-ии соб-я A без осуществления соб-я B.
4)Противо-ым соб-ю A на-я соб-е , состоящее в ненаступлении соб-я A. Ā=\A,Ā+A=
Свойства: 1)AB= ВА; AB= ВА
2)A=; A=; A Ω =А; AΩ=А;
3)(AB) С= A(B С);(AB) С= A (B С)
4)А/В=АВ-; А==А; -=; -=
5)
 =
Ā
В-;
=
Ā
В-;
=
Ā
В-;
=
Ā
В-;
4.Вер-ть случ-го соб-я. Св-ва вероятности.
Для того чтобы сравнить м/д собой соб-я по степени их возможности, необходимо связать с каждым из них некоторое число, ко-е чем больше, тем более возможно наступление соб-я. Это число наз-я веро-ю соб-я. Основное положение теории вер-ей. Пусть Е нек-й Е с дискре-м пространством элеме-х исходов
={w1,w2,…,wn} поставим в соотвюкаждому элем-му исходу wi в соотв-е число р(wi)=рi>0, кот. Назовем вероя-ю, т. о.
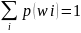
Для любого соб-я А вер-ю соб-я А назовем сумму вер-ей элемен-х исходов благоп-х этому соб-ю. А={wi1, wi2,…,win}
Р(А) =