7. Функции принадлежности. Понятие, виды.

Функция принадлежности нечёткого множества — обобщение индикаторной (или характеристической) функции классического множества. В нечёткой логике она представляет степень принадлежности каждого члена пространства рассуждения к данному нечёткому множеству.

Для пространства рассуждения   и данной функции принадлежности   нечёткое множество определяется как

Функция принадлежности   количественно градуирует принадлежность элементов фундаментального множества пространства рассуждения   нечёткому множеству  . Значение   означает, что элемент не включен в нечёткое множество,   описывает полностью включенный элемент. Значения между   и   характеризуют нечётко включенные элементы.

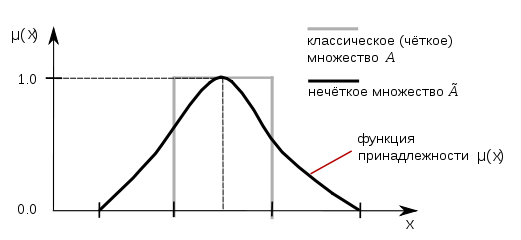
Нечёткое множество и классическое, четкое (crisp) множество

Классификация функций принадлежности нормальных нечетких множеств

Нечеткое множество называется нормальным, если для его функции принадлежности   справедливо утверждение, что существует такой  , при котором  .

Функция принадлежности класса s

Функция принадлежности класса s определяется как:

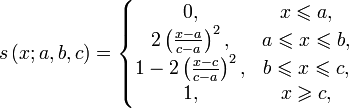
где  .

Функция принадлежности класса π

Функция принадлежности класса π определяется через функцию класса s:

где  .

Функция принадлежности класса γ

Функция принадлежности класса γ определяется как:

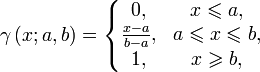
Функция принадлежности класса t

Функция принадлежности класса t определяется как:

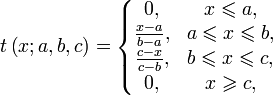
Функция принадлежности класса L

Функция принадлежности класса L определяется как:

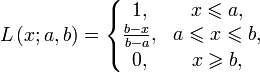
8. Правила вывода информации. Форматы отображения правил вывода.

Вывод (лат. conclusio) — процесс рассуждения, в ходе которого осуществляется переход от некоторых исходных суждений (предпосылок) к новым суждениям —заключениям.

Правила преобразования исходной системы предпосылок в систему заключений называются правилами вывода или правилами проведения умозаключений. Если вид посылок и заключений указан явно, то вывод называется прямым. Если в посылках и заключении указаны лишь виды выводов, от одного из которых разрешается переходить к другому, то вывод называют косвенным.

Понятие вывода используется во многих формальных системах: в логике, математике, информатике, логическом программировании и др. В математической логике правила логического вывода задаются в исчислении высказываний либо исчислении предикатов.

В информатике вывод умозаключений проводится с использованием правил, принципов и законов логического вывода на основе заданных фактов и правил с использованием методов и средств логического программирования.

В информатике для описания фактов и правил логического вывода, а также баз знаний и моделей экспертных систем широко используется язык логического программирования Пролог.

Умозаключения (отдельные шаги вывода) разделяют:

1. По направлению логического следования.

   1. Дедуктивные (от общего к частному).

   2. Индуктивные (от частного к общему).

   3. Трансдуктивные (от одной степени общности к такой же степени общности).

2. По достоверности вывода.

   1. Достоверные.

   2. Правдоподобные.

3. По числу посылок.

   1. Непосредственные.

   2. Опосредственные.