МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

СЕВМАШВТУЗ

ФАКУЛЬТЕТ: IV

КАФЕДРА: ФИЗИКИ

Лабораторная работа

ИССЛЕДОВАНИЕ РАБОТЫ

ИСТОЧНИКА ПОСТОЯННОГО ТОКА

Северодвинск

2002

ЛАБОРАТОРНАЯ РАБОТА №4

ИССЛЕДОВАНИЕ РАБОТЫ ИСТОЧНИКА

ПОСТОЯННОГО ТОКА

1. ЦЕЛЬ РАБОТЫ

Изучение различных режимов работы и определение к.п.д. источника тока.

МЕТОД ИЗМЕРЕНИЯ: Путём измерения силы тока, напряжения и мощности в цепи с источником тока при различных значениях внешнего сопротивления.

2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

В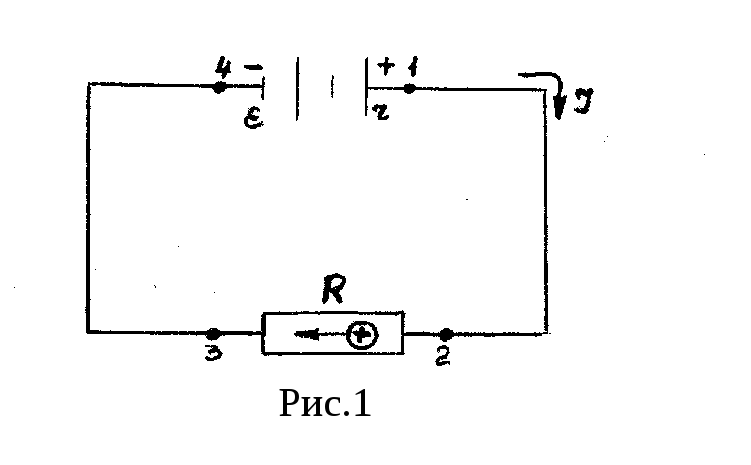 замкнутой цепи, состоящей из источника тока с внутренним сопротивлением r и проводника с сопротивлением R, будет поддерживаться постоянный ток, направленный во внешней цепи от положительного полюса к отрицательному, а внутри источника – от отрицательного к положительному.

Движение положительных зарядов внутри источника против сил электростатического поля можно объяснить только тем, что внутри источника действуют силы не электростатического происхождения. Такие силы называют сторонними. Природа их может быть механической, химической, биологической, тепловой и т.д.

Величина, численно равная отношению работы , совершаемой сторонними силами внутри источника тока при перемещении положительного заряда от одного полюса к другому, к величине этого заряда, называется ЭДС

(1)

Эта работа идёт на преодоление сопротивления среды при перемещении заряда q внутри источника и на увеличение потенциальной энергии этого заряда при перемещении, например, положительного заряда на положительный полюс, т.е. против сил кулоновского отталкивания. За счёт этой потенциальной энергии электрического поля заряд движется во внешней цепи.

Стороннюю силу , действующую на заряд q ,можно представить в виде

где – напряжённость поля сторонних сил.

Кроме сторонних сил при движении заряда по всей цепи на него действуют силы электрического поля

,

- напряжённость электрического поля.

Тогда результирующую силу, действующую на заряд в какой – либо точке цепи, можно записать в виде:

.

ЭДС можно также определить как отношение полной работы, совершаемой при перемещении положительного заряда по всей замкнутой цепи, к величине этого заряда

(2 )

При этом можно показать, что полная работа А по замкнутой цепи равна работе сторонних сил:

,т.к. сторонние силы действуют только внутри источника на участке 4-1 (рис.1).

, т.к. циркуляция вектора напряженности электрического поля равна нулю ввиду потенциального характера этого поля.

Таким образом, ЭДС равна работе, совершаемой сторонними силами по перемещению единицы положительного заряда внутри источника тока или равна полной работе, совершаемой по перемещению единицы положительного заряда по всей замкнутой цепи.

При этом важно иметь в виду, что во внешней цепи силы электрического поля совершают над положительным зарядом положительную работу А_{1,2,3,4 ,} действуя вдоль перемещения заряда, а внутри источника – такую же по величине отрицательную работу, действуя навстречу перемещению заряда. Сторонние силы внутри источника уравновешивают силы электрического поля и ещё перемещают заряд от отрицательного полюса к положительному, преодолевая внутреннее сопротивление, т.е. совершают работу А_4,1.

Таким образом, полная работа на замкнутой цепи:

А=А_1,2,3,4+А_4,1.

На внешнем участке 1,2,3,4, т.е. на сопротивлении R, работу А_1,2,3,4 можно выразить через разность потенциалов:

А_{1,2,3, 4} = (__)qUq, (3)

т.е. U = (₁ - ₄) = A_1,2,3,4 / q есть разность потенциалов или напряжение во внешней цепи. По закону Ома U = IR, где I - сила тока, R - сопротивление внешнего участка цепи.

Точно так же A_4,1 = (₄ - ₁)q = U_внутр q , (4)

т.е. U_внутр = ₄ - ₁ = A_4,1 / q есть разность потенциалов или напряжение во внутренней цепи, а по закону Ома U = Ir, где r -сопротивление внутреннего участка.

Следует заметить, что U  U_внутр, т. е. ₁ - ₄  ₄ - ₁ поскольку внутри источника поле электрических сил скомпенсировано полем сторонних сил.

Так как ЭДС источника

, то (5)

Т.о. ЭДС равна сумме падений напряжения на внешнем и внутреннем участке цепи.

Тогда или

Отсюда 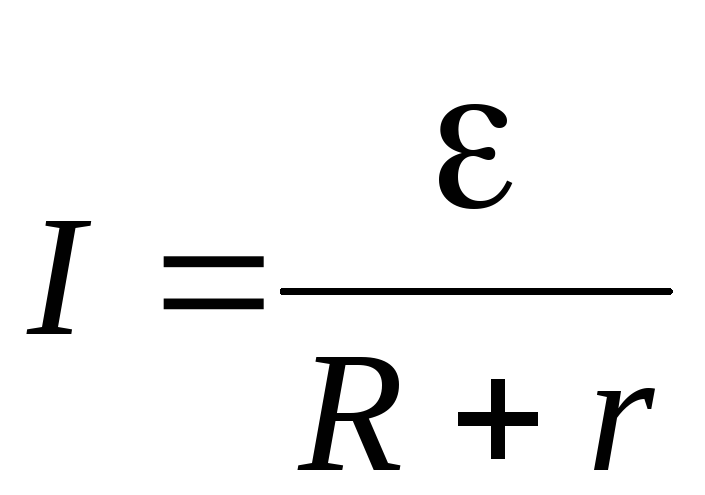- закон Ома для всей цепи.

ЭДС и падение напряжения в системе СИ измеряются в вольтах. При измерении вольтметром получим заниженное значение, т.к. вольтметр требует для своей работы наличия тока в цепи источник – вольтметр. При подключении вольтметра к зажимам источника при разомкнутой цепи он покажет U=  Ir, т.е. значение, меньшее ЭДС источника на величину падения напряжения Ir на внутреннем сопротивлении r самого источника. В тех случаях, когда внутреннее сопротивление вольтметра велико,ток в цепи вольтметра мал. Тогда   U. Для точного измерения величины ЭДС источника пользуются компенсационным методом.

Мощность (работа, совершённая в единицу времени), выделенная во всей замкнутой цепи, называется полной мощностью источника Р.

(7)

Мощность, выделенная во внешней цепи, называется полезной мощностью источника P_п.

. (8)

Отношение полезной мощности источника P_п к полной мощности P называется коэффициентом полезного действия источника.

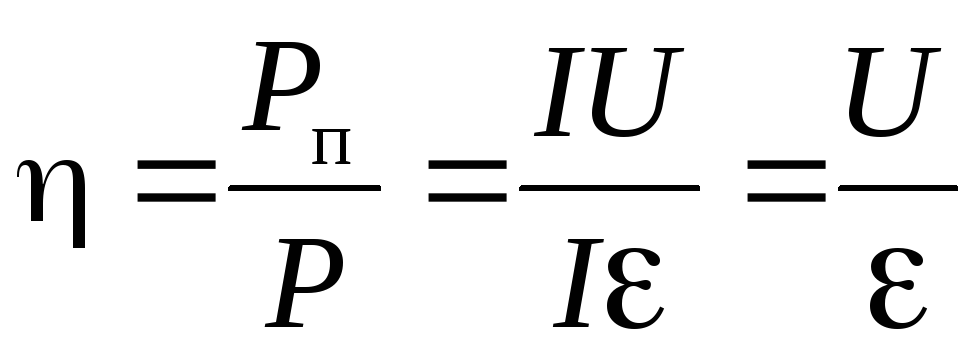(9)

При изменении величины внешнего сопротивления R меняются условия работы источника тока, что ведёт к изменению силы тока в цепи I, напряжения на зажимах с источника U, полной P и полезной P_п мощностей, к.п.д. . В зависимости от величины внешнего сопротивления R различают три режима работы источника тока:

1. Режим холостого хода при R =  /цепь разомкнута/;

2. Режим максимальной полезной нагрузки при R = r ;

3. Режим короткого замыкания при R = 0.

3. Вывод рабочей формулы

Падение напряжения во внешней цепи из уравнения ( 5 ) равно:

U = - I r . (10)

С учётом (8 ) полезную мощность P_п можно представить в виде:

P_п = IU = I(- Ir) = - I ² r + I. (11)

Из уравнения (11) видно, что полезная мощность есть функция второй степени от тока P_п =  (I ) и графически имеет вид параболы со смещённой от начала координат вершиной (рис. 2 )

Из уравнения (11) следует, что P_п дважды обращается в нуль: при I = 0 (режим холостого хода) и при  - I r = 0 , т.е. при силе тока I =  / r (режим короткого замыкания).

Взяв производную от P_п по I из уравнения (11) и приравняв её к нулю, найдём значение силы тока I , при котором полезная мощность P_п имеет максимальное значение:

= - 2 I r +  = 0, откуда I = .

Так как падение напряжения во внешней цепи равно U =  - Ir , то при I = получим: .

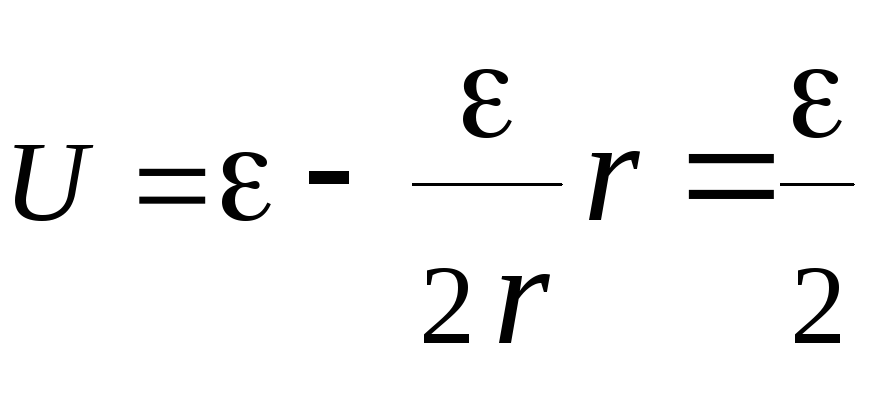Тогда по формуле (8) получим при I = максимальное значение полезной мощности P_п :

P_{п max} = IU = = (12)

По закону Ома для полной цепи . Сравнивая это выражение с I = , получим, что P_п = P_{п max} , когда внешнее сопротивление цепи R равно внутреннему сопротивлению источника, т.е. при R = r. Из выражения P = I  видим, что зависимость P =  ( I ) является линейной ( рис.2)

Из выражения 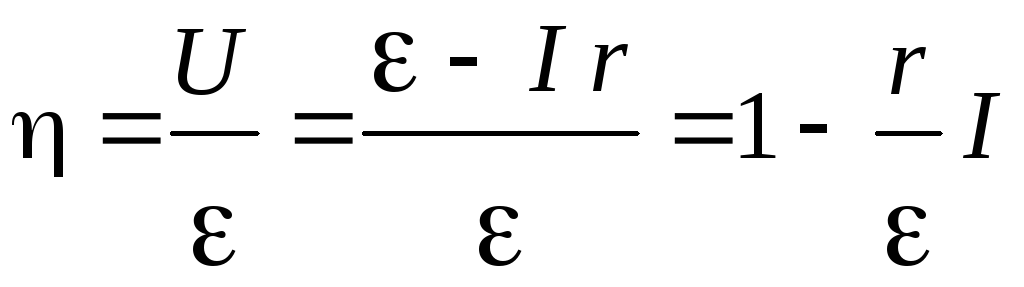видно, что зависимость  =  ( I ) является линейной (рис.2) . Очевидно, что с увеличением силы тока  уменьшается от своего максимального значения  = 1 (при I = 0) до минимального  = 0 (при I = ). При I = , что соответствует максимальному значению полезной мощности, к.п.д. становится равным:

.

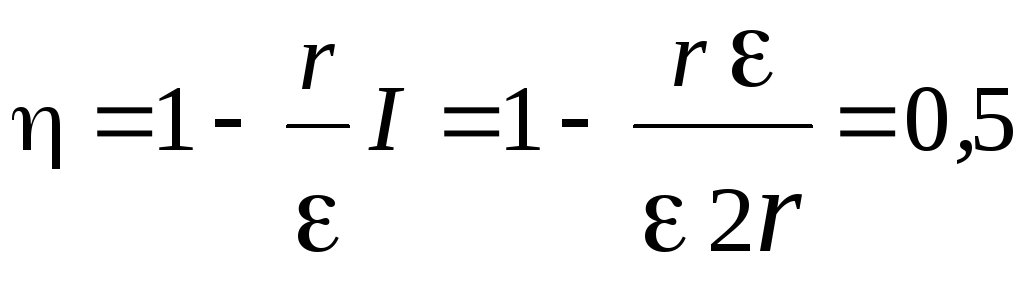Так как U = IR , то выражение (8) для полезной мощности можно записать в виде:

P_п = I ² R. (13)

Подставляя значение 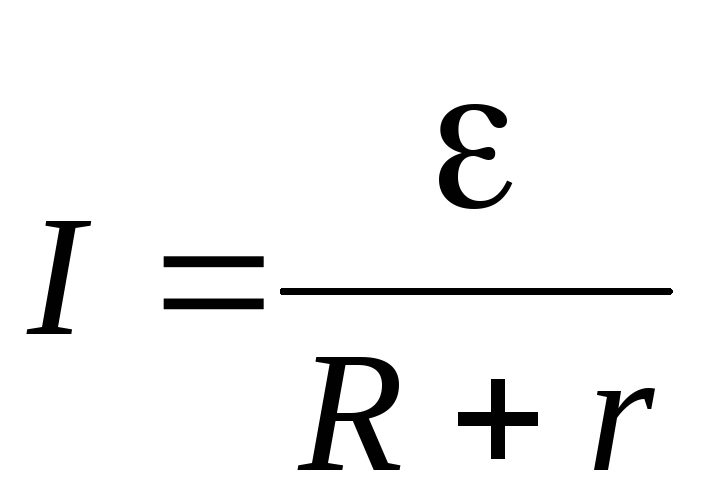, получим:

(14)

Здесь величины  и r - постоянные, следовательно, полезная мощность P_п является функцией внешнего сопротивления P_п =  ( R ) (рис.3).

Из уравнения (14) видно, что при R = 0 (короткое замыкание) и при

R =  (холостой ход) Pп = 0 . Взяв производную от P_п по R из уравнения (14) и приравняв ее к нулю, найдем значение внешнего сопротивления R, при котором P_п будет иметь максимальное значение.

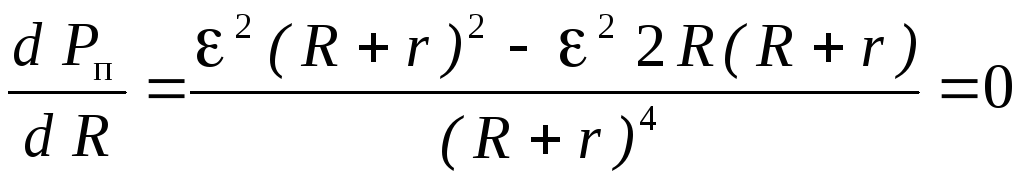
Знаменатель здесь не равен бесконечности, значит числитель должен быть равен нулю, т.е.

 ² (R + r)² -  ²2R (R + r) =  ² (R + r) (R + r – 2R) = 0.

Это равенство выполняется при R = r . Таким образом, P_п = P_{п max} , когда R = r. При этом из уравнения (14) имеем P_{п max} =.

Выражение (7) для полной мощности можно представить в виде:

(15)

Из уравнения (15) видно, что полная мощность Р принимает максимальное значение при R = 0 (короткое замыкание) , тогда P_max =. При R   полная мощность асимптотически стремится к нулю (рис.3).

К.п.д.  из уравнения (6) можно представить в виде:

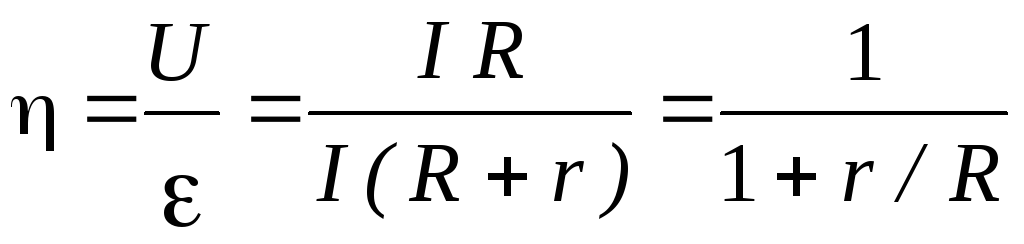(16)

Из уравнения (16) следует, что при R = 0 (короткое замыкание) к.п.д.  = 0. При увеличении R к.п.д.  возрастает и при R   (холостой ход)

  1 (рис.3). Так как полезная мощность достигает максимального значения при R = r , то в этом случае  = 0,5.

Особенности трех режимов работы источника видны из таблицы 1.

Таблица1

Режимы	I	U	Pп	P	
холостого хода	0		0	0	1
максимальной полезной нагрузки					0,5
короткого замыкания		0	0		0