45. Вихревое электрическое поле.

С переменным магнитным полем неразрывно связано вихревое индуктированное электрическое поле, которое не зависит от того, находятся в нём проводники или нет.

Характерная особенность вихревого электрического поля состоит в том, что циркуляция вектора E его напряжённости вдоль замкнутого контура зависит от выбора этого контура, т.е., в отличие от потенциального кулоновского поля, не равна тождественно нулю.

1°. Первое уравнение Максвелла в интегральной форме является обобщением закона электромагнитной индукции Фарадея в форме: .Согласно Максвеллу этот закон справедлив не только для проводящего, но и для любого замкнутого контура, мысленно выбранного в переменном магнитном поле. Это означает, что переменное магнитное поле создает в любой точке пространства вихревое электрическое поле независимо от того, находится в этой точке проводник или нет.

2°. Если воспользоваться выражением для магнитного потока, и теоремой Стокса из векторного анализа: , где dS = dS n (n – единичный вектор нормали к элементарной поверхности dS), то можно перейти от первого уравнения Максвелла в п. 1° к первому уравнению Максвелла в дифференциальной форме: . Здесь rot E в декартовых координатах выражается следующим определителем:

.

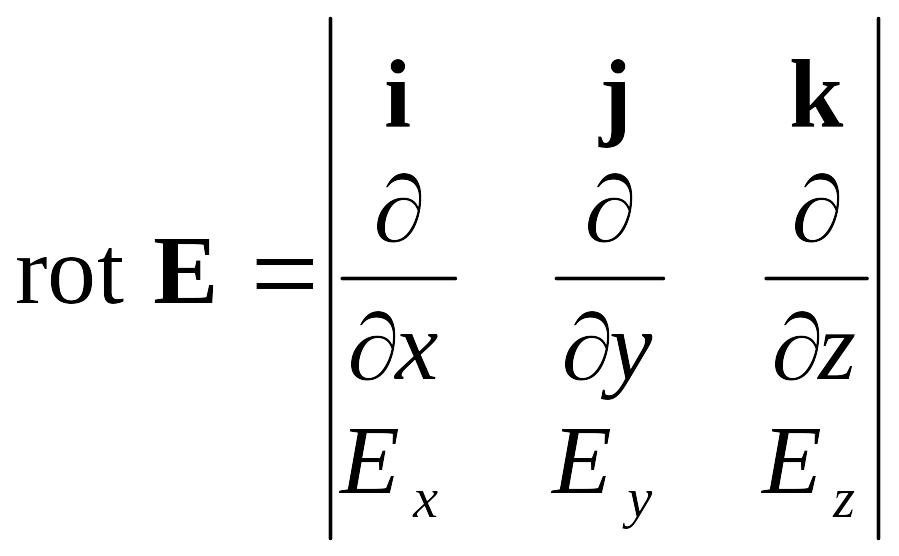3°. Возникновение в пространстве вихревого электрического поля под действием переменного магнитного поля используется в ускорителе электронов индукционного типа – бетатроне.

27. Закон Био – Савара – Лапласа. Применение закона б.-с.-л. К расчету индукции магнитн.Поля прямого тока и на оси кругового тока.

Французские ученые Био и Савар пытались получить общий закон, который позволял бы вычислять магнитную индукцию в каждой точке поля, создаваемого током, текущим по проводнику любой формы. Не удалось. Попросили Лапласа, он учел векторный характер магнитной индукции и высказал важнейшую гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиций, т.е. принцип независимого действия поля: , где dB – магнитная индукция магнитного поля малого элемента dl проводника с током, а интегрирование проводится по всей длине l проводника.

Магнитная индукция поля постоянного электрического тока в вакууме удовлетворяет закону Био-Савара-Лапласа: .

Здесь , j – плотность тока в элементе dl проводника; r – радиус-вектор, проведенный из этого элемента в проводника в рассматриваемую точку С поля(рис); k – коэффициент пропорциональности.

Вектор dB направлен в точке С перпендикулярно плоскости векторов dl и r по правилу буравчика.

Коэффициент пропорциональности k в законе Б-С-Л зависит от выбора системы единиц. В СИ это размерная величина: , где Гн/м – магнитн.постоянная. Т.о., в СИ закон Б-С-Л имеет вид: .

Так как , где - угол, под которым виден элемент dl проводника из точки С поля, то .

Из всего этого следует, что магнитная индукция поля, создаваемого в вакууме током, идущим по проводу конечной длины и любой формы, равна: .

Магнитное поле прямолинейного проводника с током.

По закону Б-С-Л, модуль вектора магнитной индукции в точке А поля элемента dl прямолинейного проводника MN: .

Где ; - расстояние от провода до точки А. Векторы dB полей всех малых элементов провода MN направлены в точке А одинаково – из-за чертежа перпендикулярно его плоскости. Это упрощает расчет В результирующего поля проводника MN. Вектор В направлен также из-за чертежа перпендикулярно его плоскости, а его модуль равен сумме модулей векторов В: 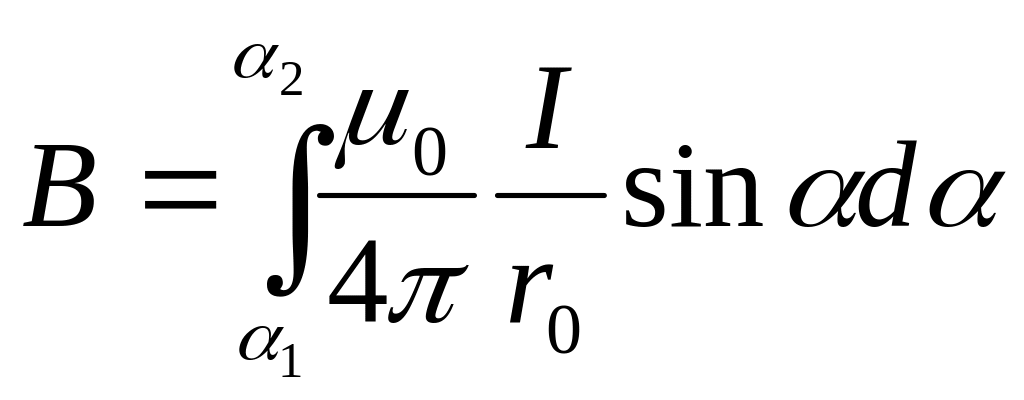. Т.о., . Если проводник бесконечно длинный, то , а и .

Магнитное поле кругового витка с током.

В центре О кругового витка радиуса r с электрическим током векторы dB магнитных полей всех малых элементов витка направлены одинаково перпендикулярно плоскости витка. Также направлен и вектор В результирующего поля всего витка. По закону Б-С-Л: , где - угол, под которым из точки О виден элемент dl витка. Интегрируя это выражение по всем элементам витка, т.е. по l от 0 до или по от 0 до : .

Определим теперь магнитную индукцию поля витка с током в произвольной точке на оси витка, т.е.на прямой , проходящей через центр витка перпендикулярно его плоскости. На рис. Показан круговой виток радиуса R, плоскость которого перпендикулярна плоскости чертежа, а ось лежит в этой плоскости. В точке С на оси векторы: для полей различных малых элементов dl витка с током не совпадают по направлению. Векторы и для полей двух диаметрально противоположных элементов витка и , имеющих одинаковую длину dl, равны по модулю: .

Результирующий вектор направлен в точке С по оси витка, причем .

Вектор В индукции в точке С для магнитного поля всего витка направлен также вдоль оси , а его модуль: .

Если воспользоваться понятием вектора магнитного момента витка с током, то можно переписать: . .