Лек. 8. Электрическое поле движущихся зарядов. Магнитное поле. Магнитная индукция. Магнитостатика в вакууме. Магнитное поле постоянного тока. Поток магнитного поля.

Взаимодействие точечных неподвижных зарядов полностью описывается законом Кулона. Однако закон Кулона недостаточен для анализа взаимодействия точечных зарядов, причем такой вывод следует не из конкретных особенностей кулоновского взаимодействия, а обусловливается релятивистскими свойствами пространства и времени и релятивистским уравнением движения. Это утверждение в принципе вытекает из соображений.

Релятивистское уравнение движения

dp/dt = F (8.1)

инвариантно и имеет одинаковый вид во всех инерциальных системах отсчета, в частности в системе координат K , которая движется равномерно и прямолинейно относительно K:

dp/dt = F (8.2)

штрихи относятся к системе K’, которая движется равномерно и прямолинейно относительно К.

в левые части этих уравнений входят чисто механические величины, поведение которых при переходе из одной системы отсчета в другую известно. Следовательно, можно связать между собой некоторой формулой левые части уравнений (8.1) и (8.2). Но тогда оказываются связанными между собой силы в правой части уравнений. Наличие такой связи обусловливается требованием релятивистской инвариантности уравнения движения. Поскольку в левые части уравнений (8.1) и (8.2) входят скорости, заключаем, что сила взаимодействия движущихся зарядов зависит от скорости и не сводится к кулоновской силе. Тем самым доказывается, что взаимодействие движущихся зарядов осуществляется не только кулоновской силой, но также силой другой природы, называемой магнитной. Выявить это можно из примера взаимодействия бесконечной заряженной нити и точечного заряда.

В системе координат К заряженная нить покоится и направлена вдоль оси (рис.21). Точечный заряд расположен на оси на расстоянии y₀ от нити. Обозначим S₀-площадь поперечного сечения нити, считая

Рис. 21.Схема взаимодействия элемента нити и точечного заряда

S₀ Если объемная плотность зарядов , то на элементе длины dx нити находится заряд dq =S₀dx. Полагаем заряд нити и точечный заряд положительными. В этом случае силы, действующие на точечный заряд со стороны заряда элемента нити, направлены как показано на рис.21

По закону Кулона

Учитывая, что

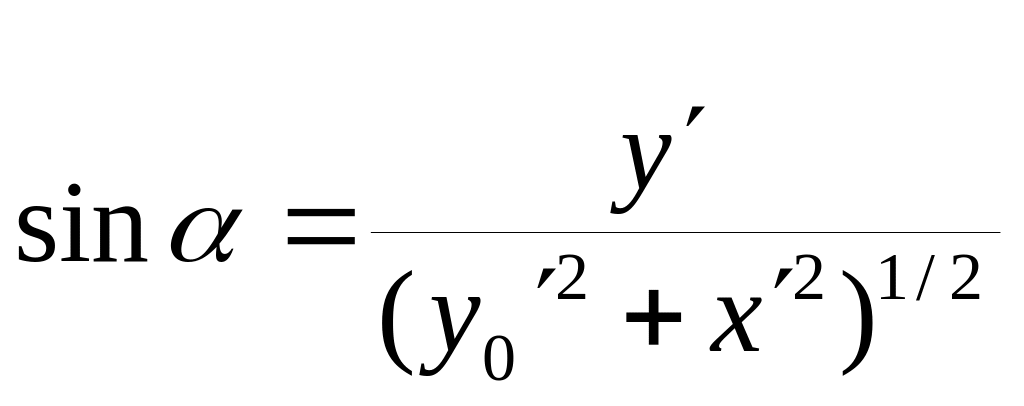
для компонент силы получаем

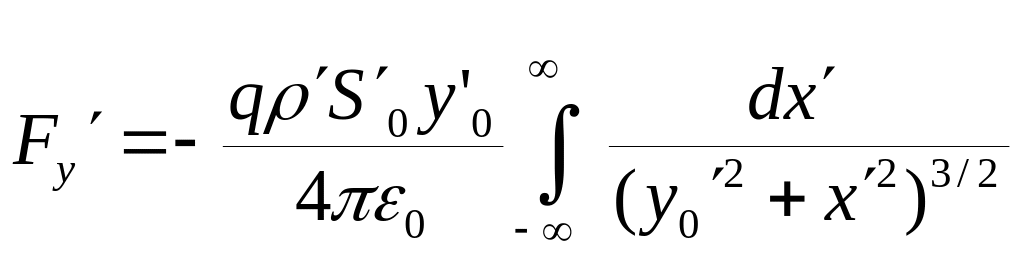
Первый интеграл равен нулю, поскольку в подыинтегральном выражении нечетная функция, а для вычисления второго интеграла используется замена переменных

x =y₀ctg dx = y₀d/sin², 1+ ctg² =1/sin², тогда

=0, = (8.5)

Кроме того, F_z=0. Принимая во внимание, что заряд в данный момент покоится

Рассмотрим это взаимодействие в системе координат К, движущейся относительно системы К со скоростью v в направлении отрицательных значений оси X. Направим ось X вдоль нити так, чтобы ее положительное направление совпадало с положительным направлением оси X, и будем считать эту систему неподвижной. В системе координат К система К, нить и заряд движутся в направлении положительных значений оси X со скоростью v. Вычислим силу кулоновского отталкивания со стороны движущейся нити на движущийся заряд. Вследствии инвариантности заряда точечный заряд q неизменен. Размеры движущейся нити сокращаются и плотность зарядов на единицу длины увеличивается

 = /1-v²/c²

Где 1-v²/c² учитывает релятивистское изменение масштабов.

Поскольку в перпендикулярном направлении скорости движения размеры остаются неизменными, то площадь поперечного сечениядвижущейся нити и расстояние от нити до точечного заряда будут неизменными.

Тогда получим

f_x=0, f_y=qS₀/(2₀y₀), f_z =0,

Используя выражение для плотности заряда, с учетом (8.5)

f_y=qS₀/(2₀y₀1-v²/c²) = qS₀/(2₀y₀1-v²/c²) = F_y/1-v²/c²), (8.9)

где S₀ =S₀, y₀ = y₀

Кулоновская сила обозначена малой буквой, чтобы отличить от полной силы, действующей на заряд которая не сводится к кулоновской силе.

Сила полная в системе координат К направлена по оси У и связана с импульсом уравнением движенеия

F_y = dp_y/dt

В системе координат К эта связь имеет вид

F_y = dp_y/dt

По формулам преобразования теории относительности

p_y = p_y,

dt/dt=1-β² /(1-vu_x /c²), β=v/c (8.12)

где u_x– компонента скорости частицыв системе координат К, причем в данном случае u_x=0.

С учетом (8.12) находим

F_y = dp_y/dt = (dp_y/dt) (dt/dt) = F_y1-β² (8.13)

Сравнивая (8.9) и (8.13)

F_y = (1-β²) f_y

Кулоновская сила отталкивания f_y больше силы F_y, действующей на движущийся заряд со стороны движущейся нити. Следовательно, кроме кулоновской силы отталкивания на заряд действует еще некая сила притяжения, отличная от кулоновской.

Разность для силы магнитной природы имеет вид

F_ym = F_y - f_y = - f_y (v²/c²)

Знак минус означает, что сила направлена к заряженной нити, т.е. сила притяжения. Эта сила второго порядка малости по v/c относительно кулоновского взаимодействия. Релятивистский эффект появления магнитного поля проявляется при любых скоростях.

Взаимодействие параллельных проводников с током.

Если заряды движутся в тонкой цилиндрической проволоке, которая в целом электрически нейтральна. Тогда кулоновские силы со стороны движущихся зврядов, образующих электрический ток, экранируются зарядами противоположного знака проволоки и вне проволоки действует лишь магнитная сила.

Следовательно, вокруг проводника с током появляется действие магнитной силы на движущиеся заряды, которые образуют электрический ток. При этом возникаем магнитное взаимодействие токов. Это получается как результат релятивистского анализа взаимодействия движущихся зарядов, хотя магнитное поле было открыто много раньше появления релятивистских представлений.

Положим, что движущие заряды представляют ток, текущий по проводнику, параллельно исходному току, текущему вдоль оси Х и расположенному на расстоянии r от него. Для исходного тока используются индексы 1, а для линейного – индексы 2. на каждый заряд тока 2 со стороны тока 1 действует сила притяжения F_my

Или в предствлении через ток

F_my = - = - = - (8.16)

где I₁=qvS₀, r = y₀

Обозначим n₂ линейную концентрацию зарядов на втором проводнике. На элементе длины dx₂ находится dq₂ = n₂dx₂ зарядов, на которые действует магнитная сила

dF_m = F_my n₂dx₂ (8.17)

подставляя в (8.17) выражение (8.16)

dF_m=- n₂dx₂ (8.18)

где I₂ = qvn₂. Кроме того, в теории магнетизма принято использовать магнитную постоянную вместо μ₀ = 1/₀c²

Тогда

dF_m = - dx₂ (8.19)

это выражение характеризует взаимодействие прямолинейных токов в бесконечных параллельных проводниках. Условие применимости - малость поперечных размеров проводников по сравнению с расстоянием между ними.

Единица силы тока. Из (8.19) видно, что на длину l₂ проводника приходится сила

F_m = - l₂ (8.20)

Знак минус показывает, что при одинаковых направлениях токов 1 и 2 между проводниками действует сила притяжения. Если направления токов различны, то возникает сила отталкивания. Из (8.20) следует определение единицы силы тока – ампер- сила тока, которая в параллельных проводниках бесконечной длины на расстоянии 1м в вакууме, вызывает силу 2 10^-7 Н на метр длины. Отсюда следует, что μ₀ =410^-7 Н/А².

Сила Лоренца. Сила Ампера.

Рассмотрим взаимодействие зарядов в системе координат К, движущейся относительно системы К со скоростью v в направлении положительных значений оси X.

В общем случае проекции сил в различных системах координат не равны между собой. Однако, между ними имеются определенные соотношения, обеспечивающие инвариантность уравнений движения, т.е. их одинаковый вид в различных системах координат

dp_x/dt = F_x, dp_y/dt = F_y , dp_z/dt = F_z (9.1)

dp_x/dt = F_x, dp_y/dt = F_y, dp_z/dt = F_z. (9.2)

Левые части этих уравнений преобразуем с помощью формул теории относительности для импульса и преобразований Лоренца

p_y = p_y p_z = p_z (9.3)

Где E= mc² –полная энергия материальной точки, β=v/c.

Формулы приводятся к виду

F_x =dp_x/dt =(dp_x/dt) (dt/dt)= =

= F_x + + (9.4)

F_y =dp_y/dt = (dp_y/dt) (dt/dt) = (9.5)

F_z =dp_z/dt = (dp_z/dt) (dt/dt) = (9.6)

Где u_x, u_y, u_z - скорости точки в системе K; F_x, F_y, F_z вошли в правые части уравнений в результате использования уравнений движения (9.2). При вычислении(9.4) принята во внимание формула

dE/dt = Fu (9.7)

выражающая закон сохранения энергии в системе координат K. С помощью формул сложения скоростей

(9.8)

Выражение (9.4) приведем к виду

F_x = F_x + + (9.9)

Для упрощения (9.5) и (9.6) необходимо важное соотношение, которое получается из формул для преобразования скоростей. Запишем прямые и обратные преобразования, например, у-проекции скорости

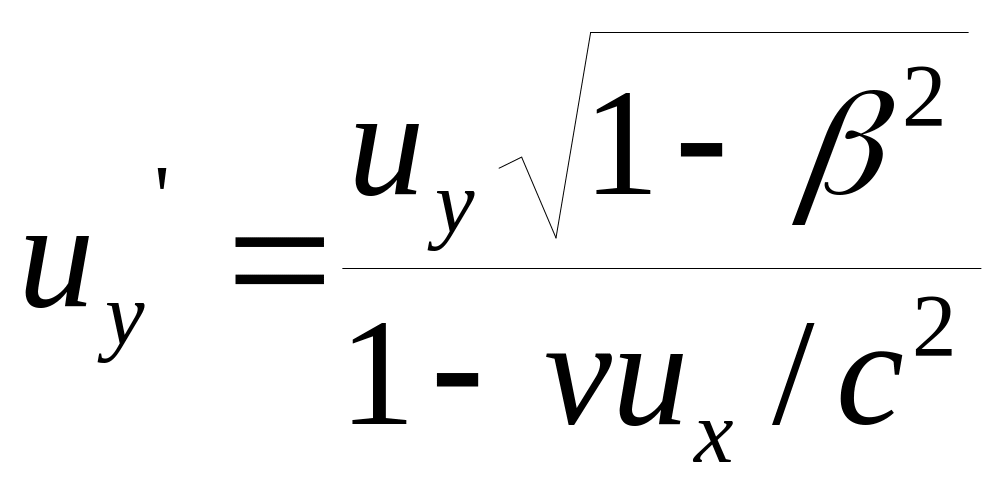
Перемножая почленно левые и правые части этих равенств и сокращая полученные равенства на общий множитель u_уu_y находим

(1+v u_x/c²)/(1-v u_x/c²)=1-β². (9.10)

Учитывая (9.10), преобразуем формулы (9.5) и (9.6)

F_y = (9.11)

F_z = (9.12)

Таким образом, с помощью формул (9.9), (9.10) и (9.12) сила в системе координат К выражена через силу в системе К. По принципу относительности можно написать и обратные преобразования.

Запишем формулы преобразования сил в векторной форме. Введем обозначения

Z = (F_x, F_y/1-β², F_z/1-β²) (9.13)

G=[0, - (v/c²) F_z/1-β²), (v/c²) F_x/1-β²)] (9.14)

Нетрудно проверить, что с помощью (9.13) и (9.14) формулы (9.9) (9.11) и (9.12) записываются в виде векторного равенства

F =Z + u× G (9.15)

Так как F – вектор, то и вся правая часть-вектор. Равенство справедливо для произвольных u. Следовательно, каждое из слагаемых в правой части является вектором. Поскольку

u× G и u –векторы, то и G тоже вектор. Таким образом, определяемые равенствами (9.13) и (9.14) величины Z и G являются векторами.

Сила Лоренца.

Положим, что в системе координат K имеется только электрическое поле и, следовательно, сила (F_x F_y F_z) не зависит от скорости u частицы. Тогда Z не зависит от скорости частицы u частицы и представляет собой электрическую силу в системе координат K.

Аналогично вектор G также не зависит от скорости u частицы, а может зависеть лишь от координаты и времени. Поэтому зависимость силы от скорости частицы содержится во втором слагаемом (9.15)

F = u× G

Это магнитная сила, направленная перпендикулярно скорости частицы и вектору G , представляющему магнитное поле, которое действует на движущуюся частицу. Поскольку Z в формуле (9.15) представляет электрическую силу, действующую на заряд q, то напряженность

Е = Z/q

Аналогично индукция магнитного поля

B = G/q

С учетом предыдущих формул, сила, действующая на заряд, записывается в форме

F= qE + qu× B

Это сила Лоренца. Первое слагаемое определяет силу электрического взаимодействия, второе – действие магнитного поля.

МАГНЕТИЗМ

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ТОКИ

5.1. Сила Лоренца

Магнитное поле - это особый вид материи. Подобно тому, как элек­трическое поле проявляет себя действием на заряды, магнитное поле проявляется в том, что на движущиеся заряды и электрические токи в этом поле действуют силы. Количественной характеристикой магнитно­го поля служит вектор магнитной индукции В. Если в пространстве существует магнитное поле, то в каждой его точке Р(r) имеется вектор В, который может изменяться с течением времени:

(5.1)

В = B(t, r).

Магнитное поле называется постоянным, когда магнитная индукция В

от времени не зависит. Если вектор В не зависит от радиус-вектора r, то магнитное поле называется однородным (рис. 5.1).

Опытным путем была установлена формула, которая описывает дей­ствие магнитного поля на движущийся со скоростью v электрический за­ряд q. Сила, с которой магнитное поле действует на движущийся заряд, называется силой Лоренца. Эта сила коллинеарна векторному произве­дению вектора скорости на вектор магнитной индукции:

(5.2)

По определению векторного произве­дения модуль силы Лоренца

F = | q | v В sin a , (5.3)

где а - угол между векторами v и В . Формулу (5.2) можно рассматривать как определение вектора магнитной индукции. Единицей измерения магнитной индукции в СИ служит тесла (T): [В] = Т = Н с/(Кл м) = кг/(с²А).

Согласно формуле (5.2) сила Лоренца, действующая на заряд в маг­нитном поле, перпендикулярна и вектору скорости v заряда, и вектору В индукции магнитного поля (рис. 5.2). При этом скалярное произве­дение вектора скорости на вектор силы Лоренца,

vF =0,

т.е. мощность силы Лоренца равна нулю. Отсюда следует, что сила Лоренца работу не совершает и кинетическая энергия частицы при ее движении в магнитном поле со временем не изменяется.

Рис. 5.2. Сила Лоренца

5.2. Движение заряженной частицы в однородном и постоянном магнитном поле

Пусть в пространстве существует однородное и постоянное магнитное поле. Такое поле характеризуется в любой точке пространства одним и

тем же вектором В . Построим систему координат так, чтобы ось у совпа­дала по направлению с вектором В магнитной индукции. При этом две проекции В_х и В_z вектора В будут равны нулю: В {0, В, 0}. Исследуем движение заряженной частицы в таком

Запишем второй закон Ньютона:

mv = q [ v В ] , (5.4)

где m, q - масса и заряд частицы.

Проекции вектора [v В ] на оси координат можно найти по известному правилу из векторной алгебры:

= =

При помощи этого выражения запишем второй закон Ньютона в проек­циях на оси координат:

mv_x = - q В v_z , т v_y = 0 , mv_z = q В v_x . (5.5)

Решив эту систему уравнений, можно найти при заданных начальных условиях зависимость от времени вектора скорости частицы: v = v(t), a затем из уравнения r = v - зависимость r = r(t), описывающую движение частицы.

Задача. Решить систему уравнений (5.5). Найти зависимость r = r(t) при произвольных начальных условиях. Показать, что траекто­рией движения заряда в магнитном поле является винтовая линия.

Согласно формуле (5.2) сила Лоренца равна нулю, когда вектор скоро­сти коллинеарен вектору магнитной индукции. Поэтому вдоль силовой линии однородного магнитного поля заряженная частица движется равномерно и прямолинейно:

F = 0 , v = const .

Направим ось у вдоль силовых линий магнитного поля (рис. 5.3). В таком случае координата у заряженной частицы будет изменяться со временем по закону

y(t)=y₀+vt

Рис.5.3. Вдоль силовой линии однородного магнитного поля заряженная частица движется равномерно и прямолинейно

Пусть в начальный момент времени t = 0 скорость заряда была пер­пендикулярна вектору В : v_y(0) = 0. При этом из второго уравнения системы (5.5) следует, что v_y(t) = 0, т.е. частица все время будет дви­гаться в плоскости перпендикулярной вектору В : v  В . Так как сила Лоренца работу не совершает и кинетическая энергия частицы со вре­менем не изменяется, модуль вектора скорости также постоянен. В этом случае тангенциальное ускорение а_т = v будет равно нулю, а нормальное ускорение в силу второго закона Ньютона будет

а_п =|q|vB/m

В

(5.6)

Рис. 5.4- Когда скорость за­ряженной частицы перпенди­кулярна силовым линиям одно­родного магнитного поля, она движется по окружности

Видно, что в постоянном и однород­ном магнитном поле нормальное уско­рение заряженной частицы со

време­нем не изменяется. Это означает, что частица будет двигаться по окружно­сти (рис. 5.4). Радиус

R этой окруж­ности найдем при помощи формулы для центростремительного ускорения

а_п =v²/R (5.7)

Приравняем правые части равенств (5.6) и (5.7). Получим:

R= т v/(|q|B)

В общем случае заряженная частица в однородном магнитном поле мо­жет совершать два вида движений. Во-первых, частица может двигаться равномерно с некоторой скоростью v||_ вдоль прямой, которая является силовой линией магнитного поля. Во-вторых, частица может двигаться с постоянной скоростью v_ по окружности, которая расположена в плос­кости, к которой силовые линии магнитного поля перпендикулярны. Эти два движения частица может совершать одновременно. В таком случае траекторией движения частицы будет винтовая линия (рис. 5.5). Эта линия характеризуется такими параметрами, как радиус R и шаг h, т.е. наименьшее расстояние между двумя точками на этой линии, отсчитан­ное вдоль ее оси. При этом проекции v||_ и v_ вектора скорости v будут связаны с его модулем и углом а между ним и вектором В соотношени­ями

v|| = v cos a , v = v sin a .

Время Т, за которое частица совершает один оборот по винтовой ли­нии, называется периодом обращения. За это время, двигаясь по окруж­ности со скоростью v , она пройдет путь 2R, а при движении вдоль силовой линии со скоростью v|| - путь h:

2 R = v Т, h = v|| Т .

Радиус R винтовой линии связан со скоростью v± соотношением

R=m v//(|q|B)

V

Рис. 5.5. Траектория движения заряженной частицы в однородном и постоянном магнитном поле - винтовая линия

5.3. Действие магнитного поля на проводник с током. Сила Ампера

Рассмотрим прямолинейный участок проводника с током, помещенно­го в пространстве, где имеется однородное магнитное поле. Электриче­ский ток есть направленное движение заряженных частиц, называемых носителями тока. На движущийся в магнитном поле заряд действует сила Лоренца.

Сумма всех сил Лоренца, которые действуют на носители тока в проводнике, может быть преобразована к виду(5.8)

(5.8)

где I - сила тока, текущего в проводнике; l - вектор, направление которо­го совпадает с направлением тока, а модуль равен длине l рассматрива­емого участка проводника (рис. 5.6). Сила F , определяемая формулой (5.8), называется силой Ампера. Согласно определению векторного про­изведения сила Ампера перпендикулярна векторам l и В , а ее модуль

F= IlВ sin a ,

где а - угол между векторами l и В . Сила Ампера не приложена к какой-либо точке проводника, а распределена по его объему.

Формулы (5.8) и (5.9) справедливы только в том случае, когда прямой проводник находится в однородном магнитном поле. Чтобы найти в об­щем случае силу, которая действует на тонкий провод с током в магнит­ном поле, разделим его на небольшие участки. Каждый такой участок можно считать прямолинейным, а магнитное поле в нем - однородным.

По формуле (5.8) найдем силу Ампера dF , которая действует на один из участков провода:

(5.10)

где dl - векторный элемент участка провода. Сила, с которой магнит­ное поле действует на тонкий провод с током, равна криволинейному интегралу

Рис. 5.6. Сила Ампера

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ТОКИ (продолжение)

5.4. Контур с током в магнитном поле

Пусть прямоугольная плоская проволочная рамка (контур) с током

находится в однородном магнитном поле В {0, В, 0} (рис. 5.7,а). Вер­тикальная сторона рамки равна а, горизонтальная - b. Силы Ампера, действующие на вертикальные стороны рамки, равны по величине 1аb, где I - сила тока. Эти силы образуют пару, момент которой равен

М = Fb sin a = I аbВ sin a ,

где а - угол между единичным вектором п, перпендикулярным плоскости

контура, и вектором В индукции магнитного поля. Примем следующее условие. Пусть направление вектора п будет связано с направлением тока в рамке правилом правого винта. Введем вектор

p_m = I Sn , (5.13)

где S - площадь рамки. В данном случае S = аb. Вектор р_т называется магнитным моментом рамки с током.

а )

б)

Рис. 5.7.

Используя формулы (5.12), (5.13) и определение вектора момента си­лы, запишем для этого вектора выражения:

(5.14)

М = [р_т В ]

M = p_mBsina. (5.15)

Из этих формул следует, что магнитное поле стремится повернуть рамку с током в такое положение, в котором векторы р_т и В направлены в одну сторону и угол а = 0 (рис. 5.7,b).

Пусть момент инерции рамки равен J. Запишем основное уравнение вращательного движения рамки

J dw/dt = - p_т В sin а (5.16)

где w = а - угловая скорость рамки. Знак "минус" в правой части это­го уравнения означает, что силы Ампера стремятся повернуть рамку в положение устойчивого равновесия, когда а = 0. Умножим левую часть уравнения (5.16) на w, а правую - на

da /dt=w

и перенесем полученное справа выражение в левую часть

Jw dw/dt + p_т В sin а(da /dt)

Это равенство нетрудно преобразовать к виду

d/dt( Jw²/2 - p_т В cos а)=0

Отсюда получим

Jw²/2 - p_т В cos а= const

Это равенство выражает собой закон сохранения энергии. Первое слага­емое есть кинетическая энергия вращения рамки, а второе

Е_р = - p_т В cos a (5.17)

- потенциальная энергия контура с током в магнитном поле. Формулу (5.17) можно записать так:

(5.18)

Как следует из формул (5.17) и (5.18), когда рамка находится в по­ложении, в котором векторы р_т и В сонаправлены и угол а = 0, ее потенциальная энергия принимает наименьшее значение -р_тВ. Следо­вательно, это есть положение устойчивого равновесия.

Рассмотрим контур с током, который имеет возможность перемещать­ся в пространстве. Пусть каким-либо образом удается сохранять ори­ентацию контура такой, что вектор р_т всегда направлен так же, как и вектор В. Из формулы (5.17) следует, что при этом энергия контура

Е_р = -р_тВ. (5.19)

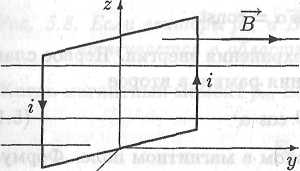
Если магнитное поле неоднородно, т.е. магнитная индукция различна в разных точках пространства, то на контур будет действовать сила, стре­мящаяся переместить его в те области пространства, где энергия контура меньше. Согласно (5.19) энергия контура меньше там, где больше маг­нитная индукция. Поэтому контур будет втягиваться в область более сильного поля (рис. 5.8).

Рис. 5.8. Если векторы р_т и В направлены сонаправлены, то контур с током втягивается в область сильного магнитного поля

Когда магнитный момент р_т направлен против поля, энергия контура

Е_p = р_тВ.

В этом случае контур будет выталкиваться из магнитного поля, т.е. на него будет действовать сила, которая стремится переместить контур в те области пространства, где поле слабее и поэтому энергия контура меньше (рис. 5.9).

Рис. 5.9. Если векторы р_т и В направлены противоположно, то контур с током выталкивается из магнитного поля