
- •21. Магнитная индукция. Сила Лоренца.
- •22. Движение заряженных частиц в постоянном магнитном поле.
- •23. Эффект Холла
- •32. Теорема Остроградского-Гаусса для магнитного поля.
- •19. Закон Джоуля – Ленца для участка цепи
- •19. Обобщенный закон Ома для участка цепи.
- •36. Магнитное поле в веществе.
- •31. Магнитное поле соленоида и тороида.
- •37. Намагниченность.
- •33. Электромагнитная индукция. Закон Фарадея-Ленца.
- •39. Напряженность магнитного поля.
- •34. Явление самоиндукции. Индуктивность. Индуктивность соленоида и тороида.
- •26. Магнитное поле постоянного тока.
- •22. Магнитное поле.
- •25. Контур с током в магнитном поле.
- •28. Магнитный момент.
- •48. Уравнения Максвелла. Материальные уравнения.
- •44. Энергия контуров с током. Энергия магнитного поля. Плотность энергии магнитного поля.
- •47. Условия квазистационарности. Квазистационарные токи.
- •46. Ток смещения.
- •24. Закон Ампера.
- •45. Вихревое электрическое поле.
- •27. Закон Био – Савара – Лапласа. Применение закона б.-с.-л. К расчету индукции магнитн.Поля прямого тока и на оси кругового тока.
- •24. Контур с током в магнитном поле.
- •§ III.10.5. Закон полного тока. Магнитные цепи.
- •18. Классическая теория электропроводности металлов.
- •29. Вихревой характер магнитного поля. Циркуляция магнитного поля в вакууме.
28. Магнитный момент.
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других) обусловлен существованием у них собственного механического момента — спина.
Магнитный момент измеряется в А*м2 или Дж /Тл (СИ).
Магнитный
момент плоского замкнутого контура с
током I:
![]() ,
где S
– площадь поверхности, ограниченной
контуром, n
– единичный вектор нормали к плоскости
контура,
,
где S
– площадь поверхности, ограниченной
контуром, n
– единичный вектор нормали к плоскости
контура,
![]() - вектор площадки S.
- вектор площадки S.
Если
контур с током не плоский, то натянутую
на него поверхность площадью S
разбирают на столь малые участки площадью
dS,
что каждый из них можно считать плоским.
Поэтому магнитный момент любого контура
с током равен:
![]() .
.
Вращающий
момент, действующий на рамку с током:
![]() ,
где
,
где
![]() - угол между векторами
- угол между векторами
![]() и В.
и В.
Для
произвольного замкнутого контура
магнитный момент находится из:
![]() ,
,
где ![]() — радиус-вектор,
проведенный из начала координат до
элемента длины контура
— радиус-вектор,
проведенный из начала координат до
элемента длины контура ![]() .
.
В
общем случае произвольного распределения
токов в среде:
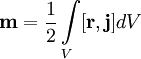 ,
,
где ![]() — плотность
тока в
элементе объёма dV.
— плотность
тока в
элементе объёма dV.
48. Уравнения Максвелла. Материальные уравнения.
Полная система уравнений Максвелла включает 4 уравнения:
![]() (1);
(1);
![]() (3);
(3);
![]() (2);
(2);
![]() (4).
(4).
Материальные
уравнения
характеризуют электрические и магнитные
свойства среды. В случае изотропных
несегнетоэлектрических и неферромагнитных
сред и макротоков, подчиняющихся закону
Ома, эти уравнения имеют вид:
![]() ,
,
![]() ,
,
![]() .
Здесь
.
Здесь
![]() и
и
![]() - электрическая и магнитная постоянные;
и
- относительные диэлектрическая и
магнитная проницаемости среды в
рассматриваемой точке поля;
- удельная электрическая проводимость
среды.
- электрическая и магнитная постоянные;
и
- относительные диэлектрическая и
магнитная проницаемости среды в
рассматриваемой точке поля;
- удельная электрическая проводимость
среды.
На
границе раздела сред должны выполняться
определенные граничные условия,
вытекающие из уравнений Максвелла.
Граничные условия для электромагнитн.поля
имеют вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
здесь
,
здесь
![]() - поверхностная плотность свободных
зарядов в точке М на поверхности раздела
сред; n
– единичный вектор нормали к поверхности
раздела, проведенный из среды 1 в среду
2(рис);
- поверхностная плотность свободных
зарядов в точке М на поверхности раздела
сред; n
– единичный вектор нормали к поверхности
раздела, проведенный из среды 1 в среду
2(рис);
![]() -
единичный вектор, касательный к
поверхности раздела сред;
-
единичный вектор, касательный к
поверхности раздела сред;
![]() - единичный вектор, касательный к
поверхности раздела сред и ортогональный
;
- единичный вектор, касательный к
поверхности раздела сред и ортогональный
;
![]() - вектор линейной плотности поверхностного
тока проводимости. Вектор
направлен вдоль поверхности по направлению
тока в ней и численно равен
- вектор линейной плотности поверхностного
тока проводимости. Вектор
направлен вдоль поверхности по направлению
тока в ней и численно равен
![]() ,
где
,
где
![]() - сила тока проводимости, проходящего
через малый участок длиной dl
сечения поверхности, проведенного
перпендикулярно направлению поверхностного
тока.
- сила тока проводимости, проходящего
через малый участок длиной dl
сечения поверхности, проведенного
перпендикулярно направлению поверхностного
тока.
1-ое
уравнение Максвелла в интегральной
форме:
![]() .
.
Циркуляция вектора E напряженности электрического поля по произвольному неподвижному замкнутому контуру равна взятой с обратным знаком скорости изменения магнитного потока через поверхность S, натянутую на этот контур.
2-ое
уравнение:
![]() .
.
![]() ,
j
– вектор плотности макротока.
,
j
– вектор плотности макротока.
2-ое
уравнение можно записать:
![]() ,
,
![]() - плотность полного тока,
- плотность полного тока,
![]() .
.
Циркуляция вектора Н напряженности магнитного поля по произвольному неподвижному замкнутому контуру L равна алгебраич. сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур.
3-е
уравнение:
![]() или
или
![]() .
.
![]() - объемная плотность свободных зарядов.
- объемная плотность свободных зарядов.
Поток смещения через произвольную неподвижную замкнутую поверхность равен суммарному свободному заряду, который находится внутри области, ограниченной этой поверхностью.
4-е
уравнение:
![]() .
.
Магнитный поток через произвольную неподвижную замкнутую поверхность, мысленно проведенную в электромагнитном поле, равен нулю.
Дифуры Максвелла получаются из интегральных с помощью 2 теорем:
Теорема
Гаусса:
![]() ,
,
![]() ,
где
,
где
![]() - проекции вектора а на оси прямоугольной
декартовой системы координат.
- проекции вектора а на оси прямоугольной
декартовой системы координат.
Теорема
Стокса:
![]() .
.
Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения охватить огромный курс явлений, начиная от электростатического поля неподвижных зарядов и кончая электромагнитной природой света.
