Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозки некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о более рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
Задача формулируется так. Имеется m
пунктов производства, в каждом из которых
сосредоточено
(
)
единиц однородного продукта. Этот
продукт нужно доставить n
потребителям, где потребность составляет
(
)
единиц. Причем
.
Известны величины
– затраты на перевозку единицы продукции
из
-го
пункта производства в
-тый
пункт потребления. Обозначим через
количество продукта, перевозимое из
-го
пункта производства в
-тый
пункт потребления. Матрица
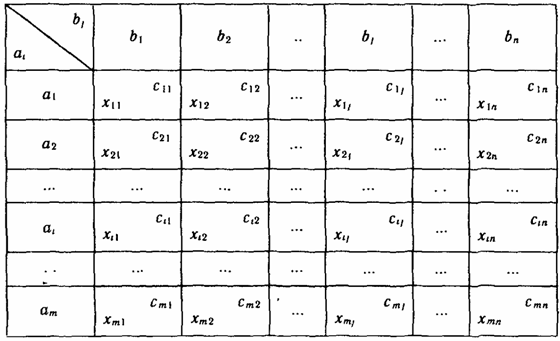
называется матрицей тарифов,
– матрицей перевозок. С целью удобства
построения математической модели
матрицы тарифов и перевозок совмещают
в одну, именуемую макетом транспортной
задачи (таблица 2).
Математическая модель транспортной
задачи: целевая функция, описывающая
транспортные затраты,
минимизируется
при ограничениях: на возможности
поставщиков – весь продукт из пунктов
производства должен быть вывезен
(
),
на спрос потребителей, который должен
быть удовлетворен:
(
),
при условии неотрицательности переменных,
исключающем обратные перевозки:
(
,
).
Таблица 2 Макет транспортной задачи
