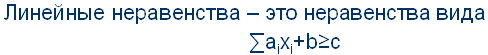- •Перечень вопросов к экзамену по дисциплине «Математика»
- •Понятие определителя матрицы. Вычисление определителей -го порядка ( ).
- •Найти точки разрыва функции и установить их род.
- •Найти частное решение дифференциального уравнения , удовлетворяющего начальным условиям
- •Решить уравнение .
- •21. Ранг матрицы
- •22. Обратная матрица
- •25. Система линейных уравнений. Теорема Кронекера-Капелли
- •28. Матричный метод решения систем линейных уравнений
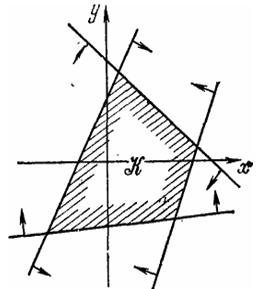
- •29. Систимы линейных неравенств. Графический метод решения систем линейных неравенств с двумя переменными
- •35. Числовые последовательности. Бесконечно малые и бесконечно большие последовательности.
- •36. Предел числовой последовательности. Свойства сходящихся последовательностей
- •37. Монотонные числовые последовательности. Экономическая интерпретация числа е
- •Монотонные числовые последовательности Понятие функции одной переменной, ее область определения и значений, способы задания и график функции
- •42. Односторонние пределы функции одной переменной
- •Исследовать график функции на характер выпуклости и перегиб.
- •Задача планирования производства продукции.
- •Задачи линейного программирования. Задача на составление смеси.
- •Графический метод решения задач линейного программирования
- •Симплекс-метод решения злп
- •Транспортная задача
Найти точки разрыва функции
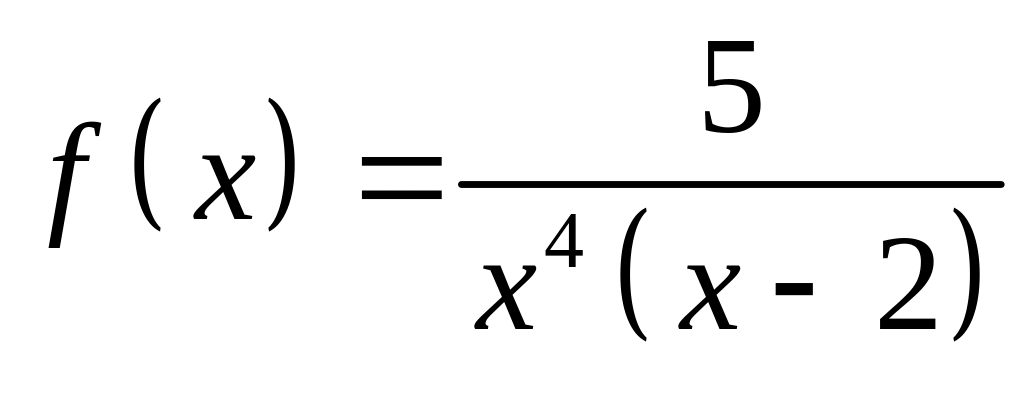 и установить их род.
и установить их род.Найти точки разрыва функции и установить их род.
Найти интервалы монотонности и точки экстремума функции
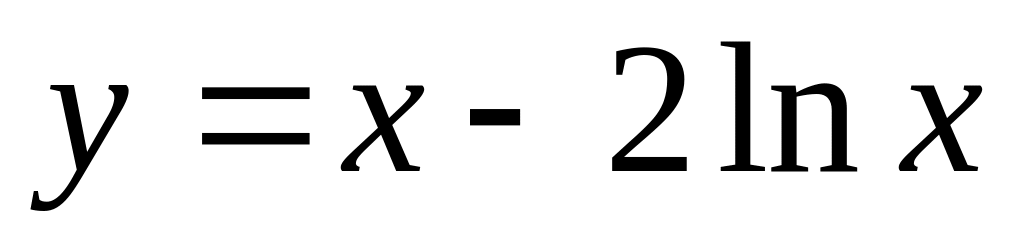 .
.Вычислить определенный интеграл:

Исследовать график функции
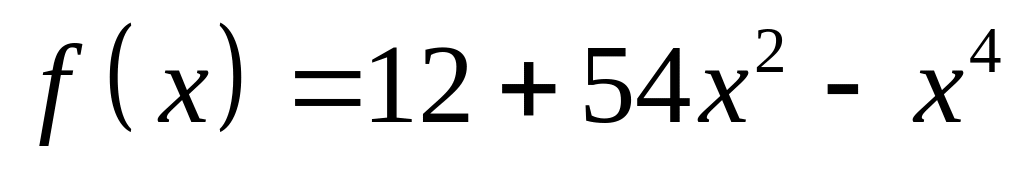 на характер выпуклости и перегиб.
на характер выпуклости и перегиб.Найти наибольшее и наименьшее значение функции
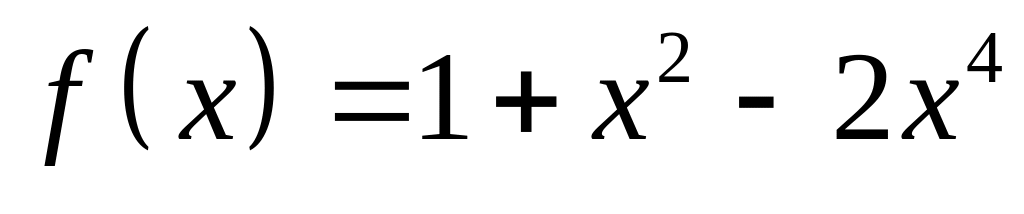 на отрезке
на отрезке
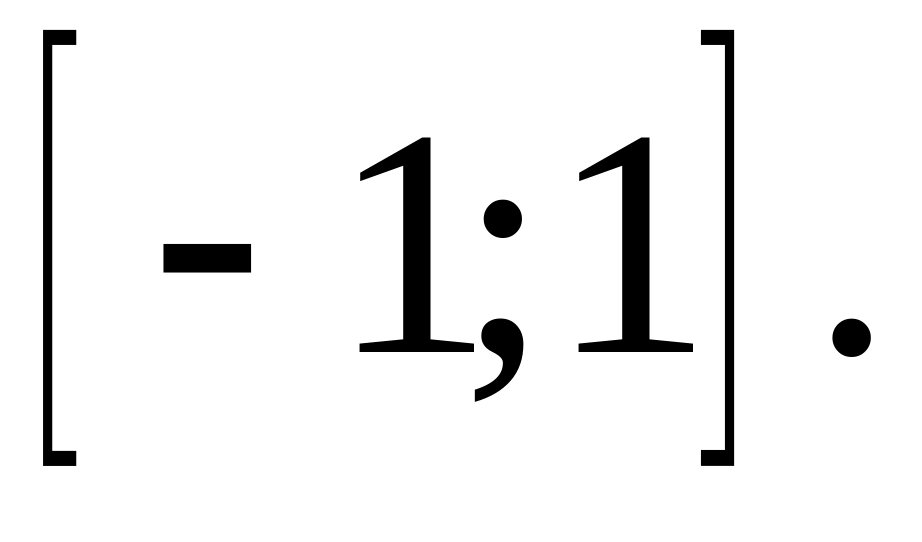
Вычислить частные производные первого порядка и полный дифференциал функции
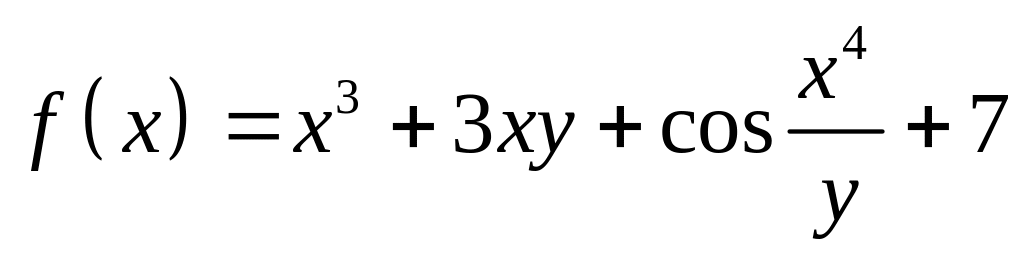 .
.Найти полный дифференциал функции
 в точке
в точке
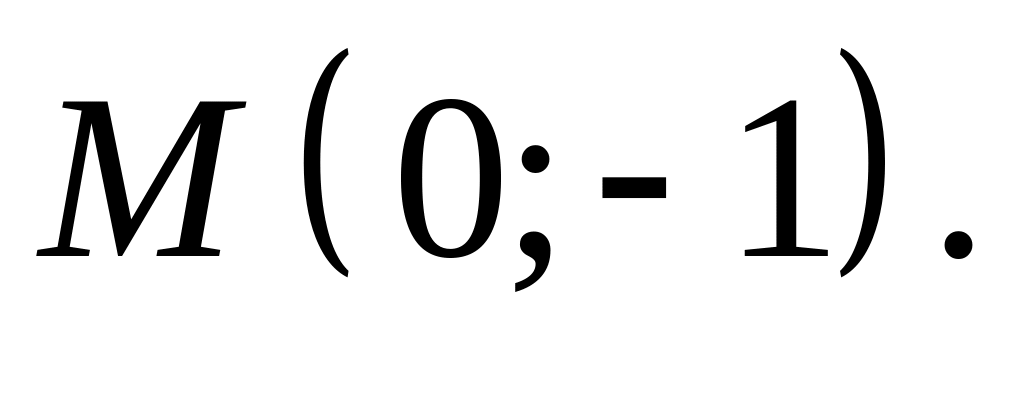
Найти частные производные второго порядка функции
 .
.Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению
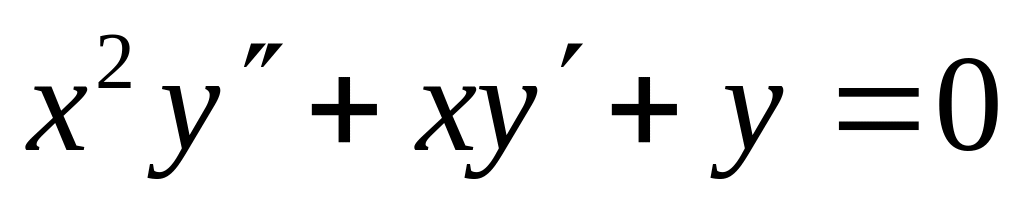 .
.Вычислить предел
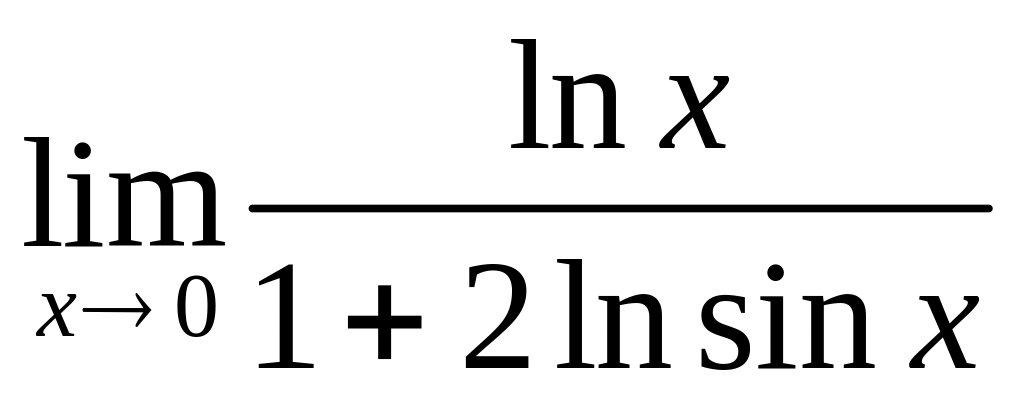 ,
используя правило Лопиталя.
,
используя правило Лопиталя.Найти неопределенный интеграл
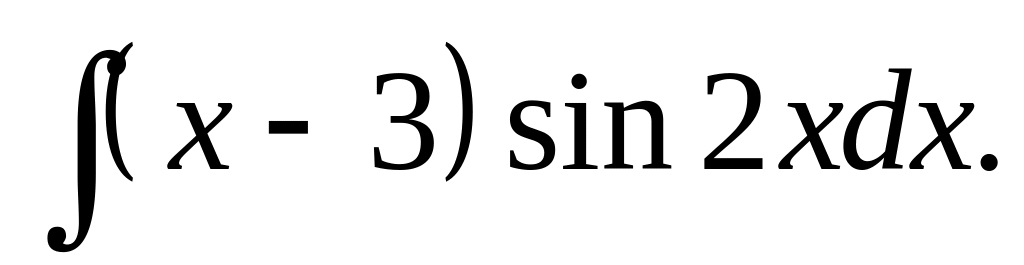
Найти определенный интеграл

Вычислить площадь фигуры, ограниченной линиями:
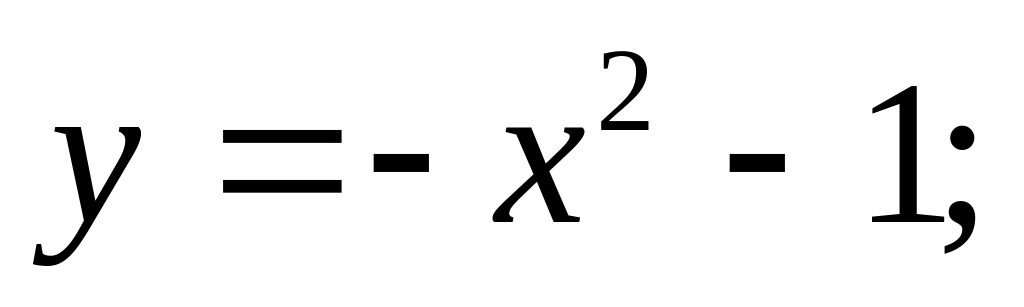
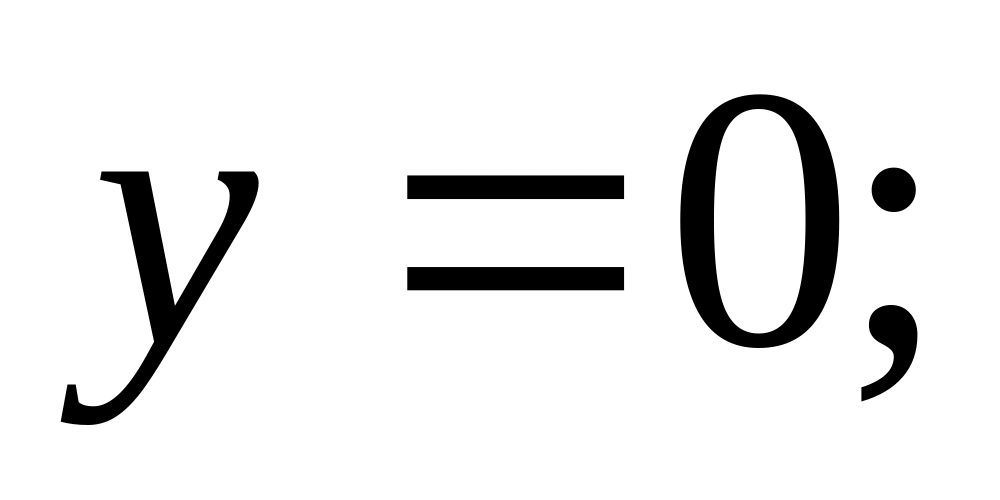
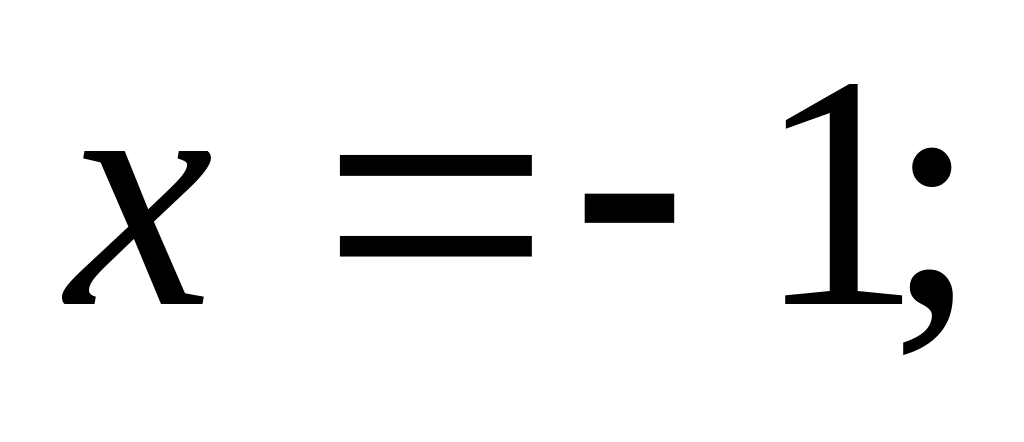
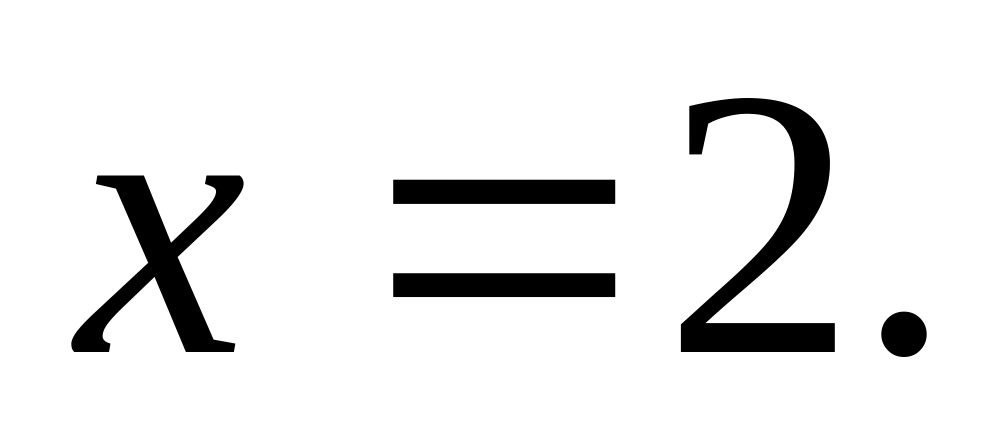
Решить задачу Коши
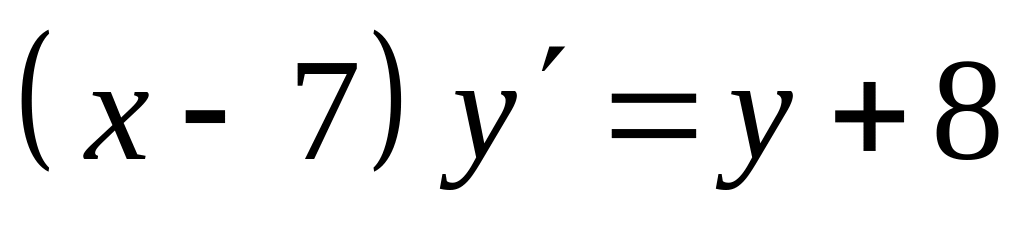 ,
,
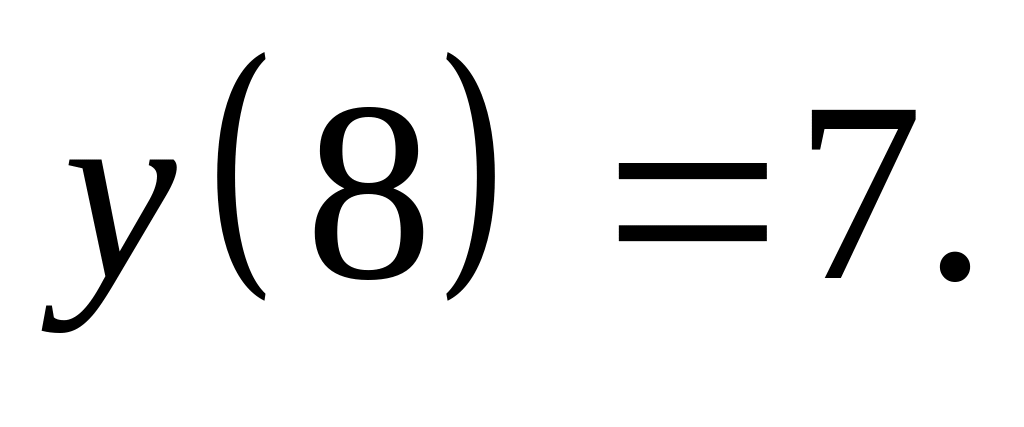
Решить дифференциальное уравнение
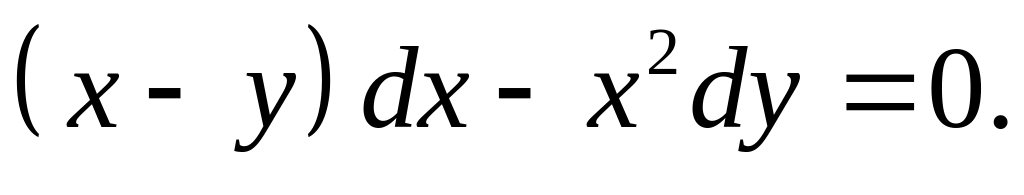
Найти частное решение дифференциального уравнения
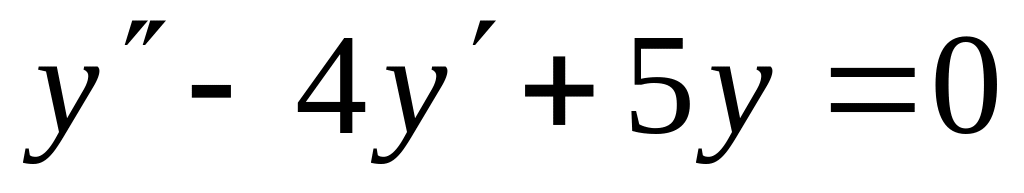 ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям
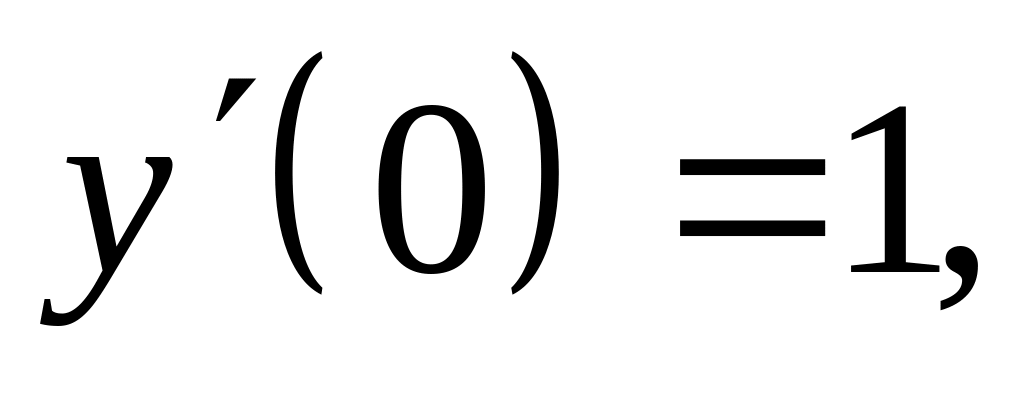
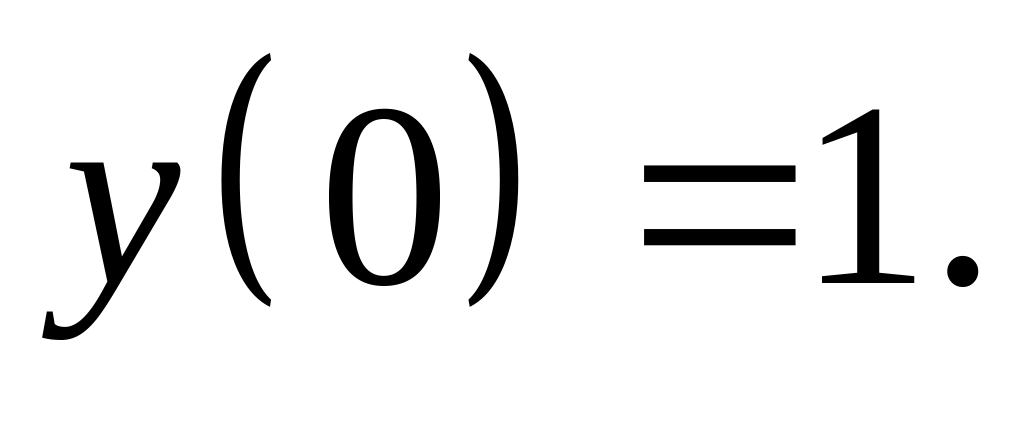
Найти частное решение дифференциального уравнения , удовлетворяющего начальным условиям
Методом математической индукции доказать, что
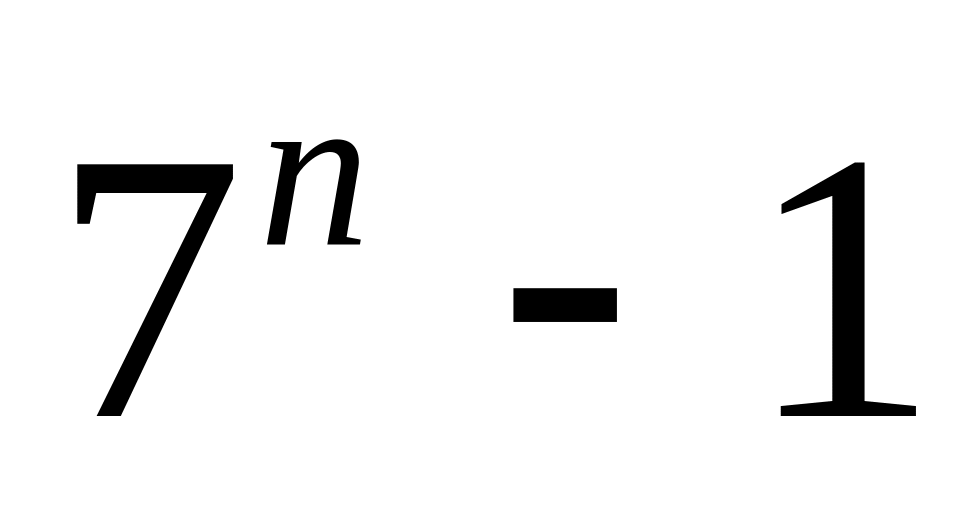 делится на 6.
делится на 6.Решить уравнение
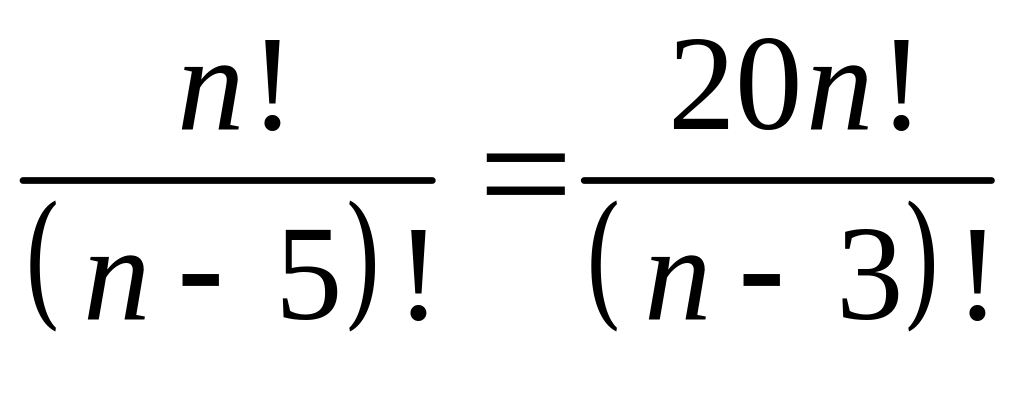 .
.Решить уравнение .
Студент пришел на зачет, зная только 35 вопросов из 50. преподаватель задает 3 вопроса. Зачет будет сдан, если студент ответит хотя бы на 2 вопроса из трех. Найти вероятность того, что студент сдаст зачет.
Из группы студентов, в которой 20 девушек и 5 юношей, для участия в олимпиаде выбирают 8 человек. Найти вероятность того, что все юноши окажутся среди участников.
Каждая из букв О, Т, Ч, А, К записана на одной из пяти карточек. Карточки раскладываются в произвольном порядке. Найти вероятность того, что при этом получается слово ТОЧКА.
21. Ранг матрицы




22. Обратная матрица
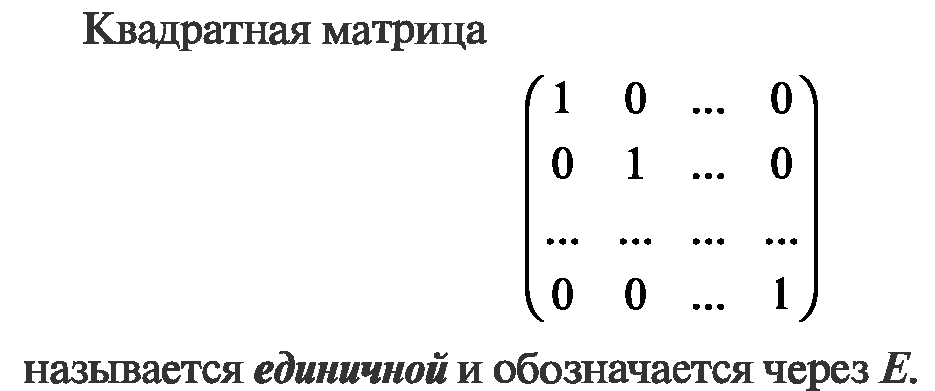

25. Система линейных уравнений. Теорема Кронекера-Капелли



Назовем расширенной матрицей системы матрицу вида
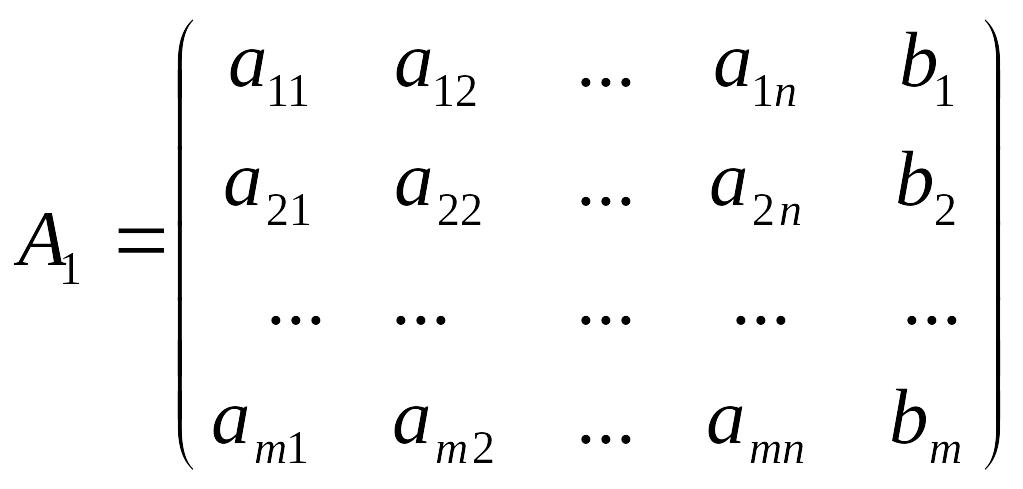 ,
,
а матрицей системы – матрицу из коэффициентов при неизвестных.
Теорема Кронекера-Капелли. Система совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.
28. Матричный метод решения систем линейных уравнений
Пусть дана система линейных уравнений
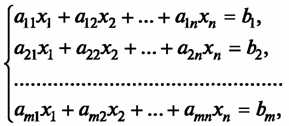
Запишем ее в
матричном виде
![]() где
где
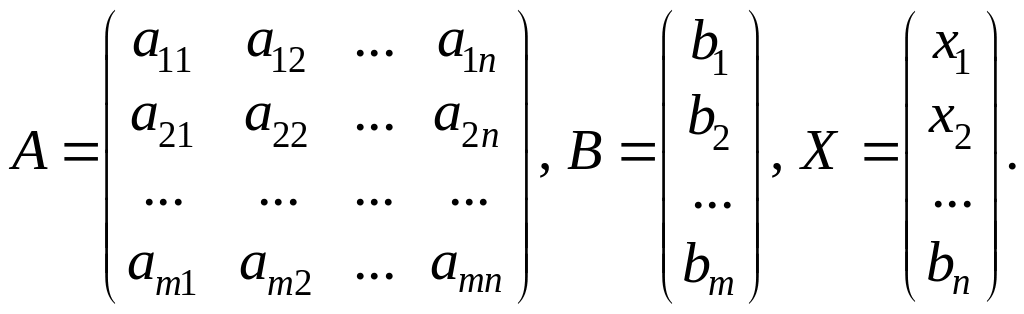
Матричный метод
решения основан на использовании формулы
![]()
Таким образом,
чтобы найти решение системы матричным
методос, сначала необходимо найти
матрицу
![]() ,
обратную к матрице А, а затем вычислить
произведение
,
обратную к матрице А, а затем вычислить
произведение
![]() ,
которое и будет искомым решением.
,
которое и будет искомым решением.
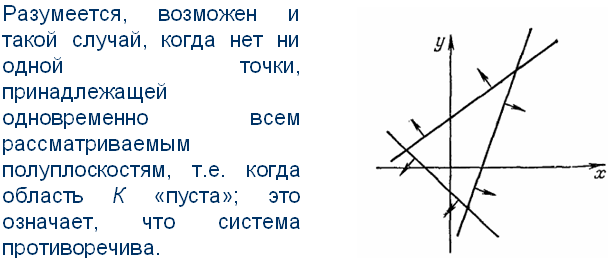
29. Систимы линейных неравенств. Графический метод решения систем линейных неравенств с двумя переменными