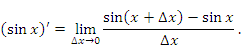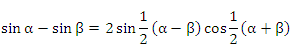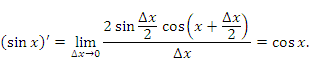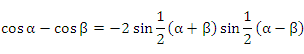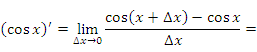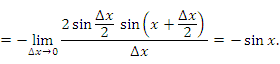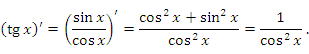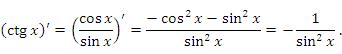45. Производная функции. Её геометрический и механический смысл.

Производной функции f(x) в точке x₀называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно мало). Записывается так.

Lim_Δx→0 (Δf(x₀)/Δx)=lim_Δx→0 ((f(x+Δx)-f(x₀))/Δx)=f`(x₀)

Функция f, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой на данном промежутке.

Геометрический смысл производной

Пусть функция   определена в некоторой окрестности   токи  , непрерывна в этой точке и  , а   (рис.2).

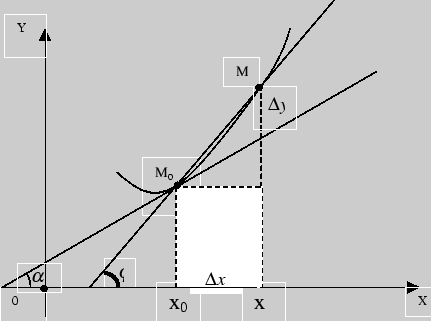
Рис. 2

Придав произвольное приращение аргументу  , так чтобы  , перейдем к точке   с абсциссой   и ординатой  , где  .

Уравнение прямой, проходящей через точки   и   (секущей графика функции  , имеет вид:  , где отношение   представляет собой угловой коэффициент секущей ( .

Касательной к графику функции   в точке   называется предельное положение секущей  , при стремлении точки   по графику   к точке  .

Для того, чтобы секущая   при   стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел  , то есть , чтобы существовала конечная производная функции   в точке  .

Угловой коэффициент касательной получается путем перехода от   к пределу при :

Таким образом, получим, что  , где   - угол наклона касательной к оси   (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции   в точке   имеет вид

В случае бесконечной производной  .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при  , получаем уравнение касательной к графику функции в точке   в виде  , то есть касательная является в данном случае вертикальной прямой, проходящей через точку   оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и   - длина пути, проходимого за время  , отсчитываемого от некоторого момента времени  .

Для определения скорости   в данный момент   придадим переменной   некоторое приращение  , при этом приращение пути будет равно  .

Отношение   называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени  , и обозначается

Предел   называется величиной мгновенной скорости движения в момент времени  .

Таким образом, мгновенная скорость в момент времени   прямолинейного движения, совершаемого по закону   равна значению производной  .

46. Производная суммы, произведения, частного.

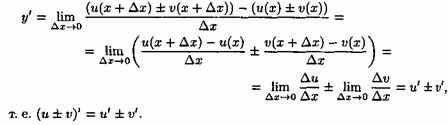
47. Производная сложной, обратной функции. Производные сложных тригонометрических функций.

Производная обратной функции

   Пусть f : [a, b] → [c, d] непрерывная, строго монотонная на интервале [a, b] функция, имеющая производную в точке х₀   [a, b]. Тогда обратная функция g = f ^-1: [c, d] →[a, b] имеет производную в точке y₀ = f(x₀) интервала [c, d] равную

,

если f '(x₀) ≠ 0. Если f '(x₀) = 0, то g '(y₀) = + ∞ (в случае, когда f возрастает), и g '(y₀) = − ∞ (в случае, когда f убывает).    Доказательство. Пусть f (x) возрастает на [a, b] и f '(x) ≠ 0. Тогда в окрестности точки y₀ = f (x₀) существует обратная функция g = f ^-1; она непрерывна и также возрастает на [c, d], в силу чего g (y) ≠ g(y₀), если у ≠ у₀. Таким образом,

.

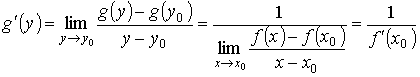Производная сложной функции

Пусть функция f: [a, b] → [c, d], а функция g:[a₁, b₁] → [c₁, d₁], причём [a₁, b₁]   [c, d]. Если функция f дифференцируема в точке х₀   [a, b], а функция gдифференцируема в точке y₀ = f (x₀)   [a₁,b₁], то сложная функция F(x) = g( f ( x )) имеет в точке х₀ производную, равную

g ' ( f ( x₀ ) )·f ' ( x₀ ).

Доказательство. Так как функция g(y) дифференцируема в точке у₀, то имеем

Δ g (y) = g ' (y₀)·Δy + δ(Δy)·Δy,

где δ(Δ х) → 0 при Δ х → 0. Так как функция f (x)дифференцируема в точке х₀, то имеем

Δ y = f ' ( x₀ )·Δx + ε (Δx)·Δx,

где ε(Δх) → 0 при Δ х → 0. Поставляя второе соотношение в первое, получим

Разделив обе части последнего соотношения на Δх, получим

.

Переходя к пределу при Δх → 0 в левой и правой части последнего равенства с учётом непрерывности рассматриваемых функций, получим

g ' ( f ( x ) )|_x0 = g ' (y₀)·f ' (x₀).

Что и требовалось доказать.

По определению производной функции Учитывая тригонометрическое тождество и первый замечательный предел, получим Вывод правила дифференцирования функции     основывается на тригонометрическом тождестве и первом замечательном пределе:   Для вывода правила дифференцирования функции     представим эту функцию в виде отношения синуса к косинусу и воспользуемся правилом дифференцирования частного от деления двух функций: 4.Аналогично обосновывается правило дифференцирования функции   :