63. Асимптоты кривых. Общая схема построения графиков функций.

Асимптоты функции

   Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.

Вертикальные асимптоты

   Вертикальные асимптоты определяются точками разрыва функции и границами области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Некоторые особенности поведения функции в окрестности вертикальных асимптот представлено на рисунке.    Вертикальные асимптоты определяются точками разрыва второго рода В этом случае f( x₀ ± 0) = ± ∞, или f ( x₀ ± 0) = + ∞ , или f (x₀ ± 0) = − ∞.    Следует отметить, что в этом случае может отмечаться всё разнообразие поведения функции в окрестности точки разрыва. Например, на рис. 8.2 приведён график элементарной функции

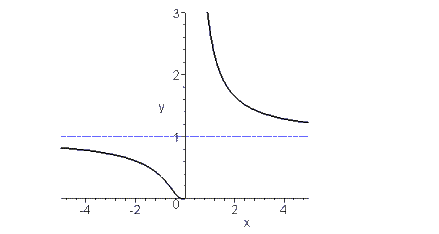. Рис. 8.2. Точка разрыва второго рода для данной функции определяется только справа

Горизонтальные асимптоты

   Если

,

то у = b — горизонтальная асимптота кривой y = f (x) (правая – при х стремящемуся к плюс бесконечности, левая – при х стремящемуся к минус бесконечности и двусторонняя, если пределы при х стремящемуся к плюс-минус бесконечности равны).

Рис. 8.3. Примеры горизонтальных двухсторонних и односторонних асимптот

Наклонные асимптоты

   Уравнение наклонной асимптоты функции y = f (x) определим уравнением y =k·x + b. При этом параметры наклонной асимптоты определяются соотношениями

, .

   Для того, чтобы функция y = f (x ) имела асимптоту y = k ·x + b, н еобходимо и достаточно, чтобы существовали указанные выше конечные пределы.    Доказательство. По определению асимптоты имеем

.

Так как MP = MP₁·cos α, где угол α есть величина постоянная, равная углу наклона асимптоты к оси Ох. Поэтому соотношение для определения асимптоты можно записать в виде

.

Так как точки М и Р₁ соответствуют одному и тому же значению аргумента, то это соотношение можно записать в виде

.                        (9.1)

Если вынести за скобки х, то

,

из этого однозначно будет следовать

,

или

.

Откуда следует соотношение для нахождения углового коэффициента асимптоты

.

Зная угловой коэффициент асимптоты, из соотношения (9.1) получим

.

Общее исследование функции и построение графика

   С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление вогнутости графика, наличие асимптот.    Обычно используют следующую схему исследования функций:

1. Определение области определения.

2. Определение четности или нечетности.

3. Определение периодичности функции.

4. Определение интервалов знака постоянства первой производной.

5. Определение интервалов знака постоянства второй производной.

6. Составление таблицы результатов.

   х
   у '
   у ''
   у

7.    В первой строчке таблицы указываются интервалы, на которые разбивается область определения функции точками разрыва, точками экстремума и точками перегиба в порядке следования. Сами эти точки в порядке следования помещаются в отдельные столбцы. Во второй строчке таблицы в каждой ячейке указываются знаки первой производной. В третьей строчке таблицы в каждой ячейке указываются знаки второй производной. В четвёртой строчке определяется характер поведения функции в каждой ячейке. Если это точки экстремума или точки перегиба, то указываются значения функции в этих точках.

8. Нахождение асимптот.

9. Построение графика функции, начинается с построения асимптот и характерных точек.

64-65. Комплексные числа и формы их представления. Алгебраические действия над комплексными числами.

Определения. Комплексным числом называется выражение вида x + y·i, в котором х и у - вещественные числа, а i – некоторый символ, если при этом приняты условия: 1) x + 0·i = х, 0 + y·i = y·i и 1·i = i, (− 1)·i = − i, 2) x + y·i = x₁ + y₁·i тогда и только тогда, когда х = х₁, у = у₁, 3) (x₁ + y₁·i) + (x₂ + y₂·i) = (х₁ + х₂) + (y₁ + y₂)·i, 4) (x₁ + y₁·i) · (x₂ + y₂·i) = (х₁·x₂ - y₁·y₂) + (х₁·y₂ + y₁·x₂)·i.    Из условий 1) и 4) получаются степени числа i:

i2 = − 1, i3 = − i, i4 = 1, и т.д.

(1)

Комплексное число x + y·i, в котором x = 0, у ≠ 0, называется мнимым числом. Символ i называется мнимой единицей.

   2°.Действия над комплексными числами. Сложение, вычитание, умножение и возведение в степень комплексных чисел можно выполнять по правилам этих действий над многочленами с заменой степеней числа i по формулам (1). Деление комплексных чисел и извлечение корня из комплексного числа определяются как действия обратные.

   3.Тригонометрическая форма комплексного числа. Комплексное число x + y·i определяется парой вещественных чисел (х, у) и поэтому изображается точкой М(х, у) плоскости или её радиус-вектором   называется модулем комплексного числа, а угол его φ с осью Ох называется аргументом комплексного числа.

Так как

x = r cos φ, y = r sin φ

то

x + y·i = r·( cos φ + i sin φ)

(2)

4°. Действие над комплексными числами в тригонометрической форме:

(3)

(4)

[r·( cos φ + i sin φ)]n = rn (cos n φ + i sin n φ)

(5)

(6)

где k = 0, 2 , 3, …. Формулы (5) и (6) называются формулами Муавра.    5.Формула Эйлера: e^i φ = cos φ + i sin φ.    6.Логарифм комплексного числа: ln z = ln r + i·φ₀ + 2 k π i , где φ₀ - значение аргумента φ, удовлетворяющее неравенствам − π ≤ φ ≤ + π. Выражение ln r + i·φ₀ называется главным значением логарифма.

66-67.

Теорема Безу

   При делении многочлена f (x) = A₀xⁿ + A₁x^n-1 + … + A_n на разность х – а получается остаток, равный f (а).    Доказательство. При делении f (x) на х – а частным будет многочлен f₁(x), степень которого будет на единицу ниже степени многочлена f (x) и остаток, который будет постоянным числом: f (x) = (х – а )·f₁(x) + R. Переходя к пределу в левой и правой части этого равенства при х → а, получим R = f(а).     Если х = а — корень многочлена, то f (а) = 0 и многочлен f (x) нацело делится на разность х – а и многочлен представляется в виде

f (x) = ( х – а )·f₁ (x),

где f₁ (x) — многочлен.

Основная теорема алгебры

   Всякая целая рациональная функция f (x) имеет, по крайней мере, один корень, действительный или комплексный.

Теорема о разложении многочлена на линейные множители

   Всякий многочлен n – ой степени разлагается на n линейных множителей вида х – а и множитель, равный коэффициенту при старшей степени xⁿ.    Доказательство. Пусть f (x) = A₀xⁿ + A₁x^{n - 1} + … + A_n — многочлен n – ой степени. Этот многочлен в силу основной теоремы алгебры имеет один корень а₁. Тогда из следствия теоремы Безу будем иметь f (x) = (х – а₁)·f₁ (x), где f₁ (x) — многочлен степени n - 1. Многочлен f₁ (x) тоже имеет корень а₂.    Тогда f₁ (x) = (х – а₂ )·f₂ (x), где f ₂ (x) — многочлен степени n – 2. Аналогично f₂ (x) = (х – а₃)·f₃ (x). Продолжая процесс выделения линейных множителей, дойдём до соотношения f_n(x) = (х – а _n )·f_n, где f_n — число (многочлен нулевой степени), и это число равно коэффициенту при хⁿ, то есть f_n = А₀. На основании всех этих равенств можно записать

f (x) = А₀·( х – а ₁)·( х – а₂)· … ·( х – а_n).

Кратные корни многочлена

   Если в разложении многочлена n – ой степени на линейные множители f (x) = А₀·( х – а ₁) ·( х – а ₂)·…·( х – а_n), некоторые линейные множители окажутся одинаковыми, то их можно объединить, и тогда разложение многочлена на множители будет иметь вид

.

При этом k₁ + k₂ + … + k_m = n. В этом случае корень а₁ называется корнем кратности k₁, корень а₂ называется корнем кратности k₂, и так далее.    Если многочлен имеет корень а кратности k, то будем считать, что многочлен имеет k одинаковых корней. Всякий многочлен n – ой степени имеет ровно nкорней (действительных или комплексных).

Разложение многочлена на множители в случае комплексных корней

   Если многочлен f (x) с действительными коэффициентами имеет комплексный корень a + i·b , то он имеет и сопряжённый корень a - i ·b. В разложении f (x) = А₀·( х – а ₁) ·( х – а ₂)· …·( х – а_n) комплексные корни входят попарно сопряжёнными парами. Перемножив линейные множители, соответствующие паре сопряжённых корней, получим трёхчлен второй степени с действительными коэффициентами

[x − (a + ib)]·[x + (a + ib)] = [(x − a) − ib]·[(x − a) + ib] = (x − a)² + b² = x² − 2 ax + a² + b² = x² + px + q

где р = – 2·а, q = а ² + b ² — действительные числа. Если число a+ i·b является корнем кратности k, то сопряжённое число a - i ·b должно являться корнем той же кратности k. Так что наряду с линейным множителем х - (a + i·b) в разложение многочлена входят столько же линейных множителей вида х - (a - i·b).    Таким образом, многочлен с действительными коэффициентами разлагается на множители вида

При этом k₁ + k₂ + … + 2s₁ + … + 2s_m = n.

Для того чтобы многочлены P_n(z) и Q_n(z) были тождественны, необходимо и достаточно, чтобы их коэффициенты при одинаковых степенях z были равны.