1. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.

Числовой ряд. Рассмотрим произвольную числовую последовательность  и составим сумму ее членов 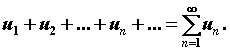    Это выражение называют числовым рядом, или просто рядом. Члены последовательности  называют членами ряда.

Сумма первых n членов ряда  . - n-ой частичная сумма.

 

Сходимость числового ряда. Ряд     называют сходящимся, если существует и конечен предел последовательности      частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают    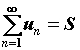,  . Если предел частичных сумм не существует или бесконечен, то ряд расходится и суммы не имеет.

Теорема 1. Если сходится ряд, получившийся из данного ряда отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.

Иными словами, на сходимость ряда не влияет отбрасывание конечного числа его членов.

Доказательство. Пусть Sn—сумма n первых членов ряда, Ck —сумма k отброшенных членов, Qn-k - сумма членов ряда, входящих в сумму Sn и не входящих в Ck. Тогда имеем: Sn= Ck + Qn-k

где Ck — постоянное число, не зависящее от n.

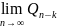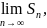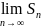Из последнего соотношения следует, что если существует , то существует и если существует , то существует , а это и доказывает справедливость теоремы.

Теорема 2. Если ряд a1 + a2 + … an сходится и его сумма равна s, то ряд

ca1 + са-2 + ...can , где с — какое-либо фиксированное число, также сходится и его сумма равна сs.

Доказательство. Обозначим n-ю частичную сумму 1 ряда через Sn, а 2 ряда— через 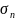. Тогда

Отсюда ясно, что предел n-й частичной суммы ряда (4) существует, так как

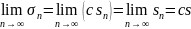
Итак, ряд сходится и его сумма равна сs.

Теорема 3. Если ряды a1+a2+… и b1 + b2 + . . . сходятся и их суммы, соответственно, равны , то ряды (a1+b1) + (a2+b2) + … и (a1 – b1) + (a2 – b2) + … также сходятся и их суммы, соответственно, равны 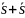и .

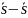Необходимое условие сходимости ряда.

Теорема.

Если числовой ряд   сходится, то его общий член при неограниченном возрастании n стремится к нулю, т.е.

Доказательство.

Пусть данный ряд сходится. Тогда по определению сходящегося ряда

;

так как вместе с   также и  , то  , т.е.

Здесь  , а  .

Поэтому 

Отсюда  , что и требовалось доказать.

Нарушение необходимого признака устанавливает расходимость ряда. Это значит, что если некоторого ряда  , то такой ряд является расходящимся. В этом случае применение необходимого признака дает законченный результат. Если же для некоторого ряда этот признак выполнен, то соответствующий ряд может быть и сходящимся и расходящимся. В таких случаях, т.е. при выполнении условия  , вопрос о сходимости ряда требует дальнейшего исследования.

Действия с числовыми рядами

Выделяют следующие действия с числовыми рядами (они имеют смысл, т.е. сохраняют сумму ряда, только если она существует):

Линейная комбинация рядов

Если ряды   и   сходятся, то сходится и ряд   (α, β — постоянные), при этом

Группировка членов ряда

Сгруппируем слагаемые ряда  , объединив без изменения порядка следования по нескольку (конечное число) членов ряда. Получим некоторый новый ряд  . Раскрытие скобок в ряде в общем случае недопустимо, однако: если после раскрытия скобок получается сходящийся ряд, то раскрытие скобок возможно; если а каждой скобке все слагаемые имеют один и тот же знак, то раскрытие скобок не нарушает сходимости и не изменяет величину суммы.

Перестановка членов ряда

Если ряд сходится абсолютно, то любой ряд, полученный из него перестановкой членов, также сходится абсолютно и имеет ту же сумму, что и исходный ряд. Если ряд сходится условно, то для любого наперёд заданного A (в том числе  ,  ,  ) можно так переставить члены этого ряда, что преобразованный ряд сходится к A (расходится к  ,  ,  ) либо не имеет предела (теорема Римана).