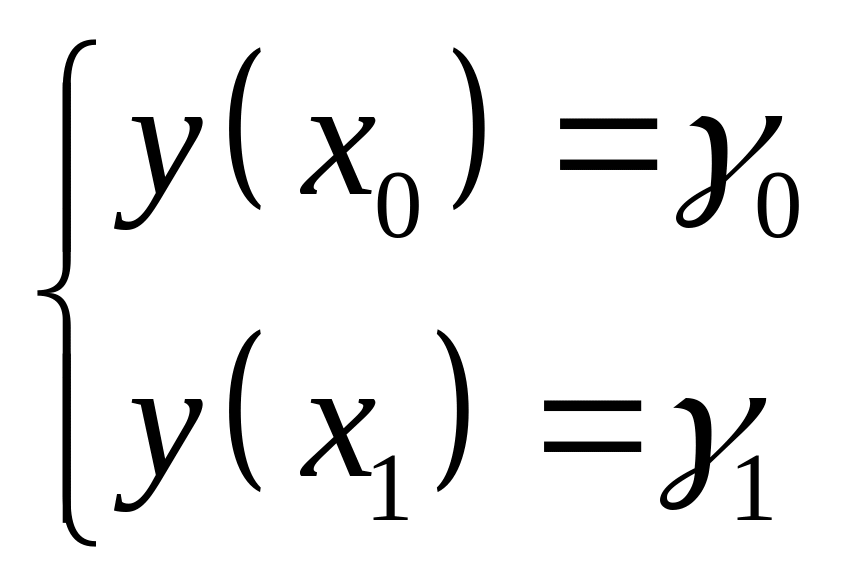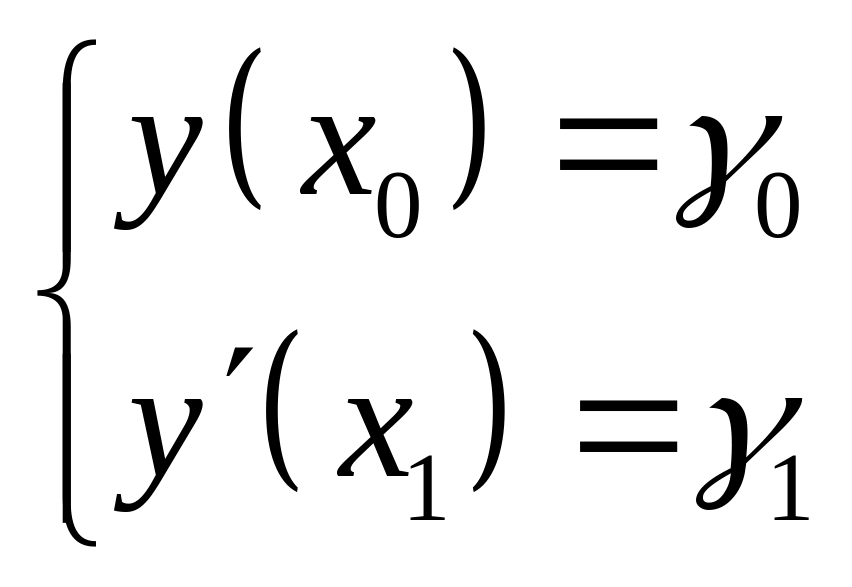- •Билет № 1
- •1°. Пример
- •2°. Определения.
- •3 °. Геометрический смысл ду.
- •4°. Задача Коши.
- •1°. Уравнение в полных дифференциалах.
- •2°. Принцип сжатых отображений.
- •3°. Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.
- •3°. Связь нормальных систем с общими дифференциальными уравнениями (оду) n-го порядка.
- •5°. Нормальная линейная система (нлс).
- •1°. Линейная однородная система (лос).
- •2°. Фундаментальная система решений (фср).
- •Фундаментальная матрица однородной системы и её свойства. Определитель Вронского.
- •3°. Определитель Вронского (Вронскиниан).
- •5°. Линейные однородные дифференциальные уравнения -го порядка.
- •Свойства уравнения :
- •4°. Линейные неоднородные уравнения - го порядка с постоянными коэффициентами и правой частью.
- •5°. Лос с постоянными коэффициентами.
- •5°. Лос с постоянными коэффициентами.
- •1°. Теорема о непрерывной зависимости решений от реальных условий.
- •2°. Устойчивость по Ляпунову. Асимптотическая устойчивость.
- •3°. Теорема Ляпунова.
- •4°. Классификация точек покоя линейных систем 2-го порядка с постоянными коэффициентами.
2°. Устойчивость по Ляпунову. Асимптотическая устойчивость.

![]() ,
,
 на
на
![]() .
.
Опред.:
Решение
![]() нормальной системы называется устойчивым
по Ляпунову,
если
нормальной системы называется устойчивым
по Ляпунову,
если
![]()
![]() той же системы, удовлетворяющее
неравенству
той же системы, удовлетворяющее
неравенству
![]() ,
,
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
,
![]() .
.
Опред.: Решение асимптотически устойчиво, если оно устойчиво по Ляпунову и
![]() ,
.
,
.
![]()
![]()
![]() .
.
Решение нормальной
системы устойчиво тогда и только тогда,
когда устойчиво нулевое решение
преобразованной системы
![]()
![]()
Билет №22
3°. Теорема Ляпунова.
Теорема:
Пусть нормальная
система
имеет решение
.
Пусть существует дифференцируемая
функция
![]() ,
удовлетворяющая условиям:
,
удовлетворяющая условиям:
1).
![]() ,
,
![]() .
.
2).
если
-
решение, то
![]() при
при
![]() ,
тогда точка покоя
,
тогда точка покоя
![]() устойчива по Ляпунову.
устойчива по Ляпунову.
Если к тому же
![]()
![]() при
при
![]() ,
,
то точка покоя
асимптотически устойчива.
,
,
то точка покоя
асимптотически устойчива.
Опред.:
Функция
![]() называется функцией Ляпунова.
называется функцией Ляпунова.
Следствие:
Если действительные
части всех собственных чисел матрицы
отрицательны, то любое решение
![]() ассимптотически устойчиво.
ассимптотически устойчиво.
Доказательство:
,
![]() -
собственные числа матрицы
.
-
собственные числа матрицы
.
Если
![]() ,
,
![]() .
.
 .
.
Билет № 23
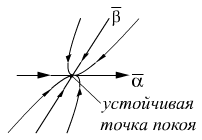
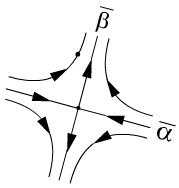
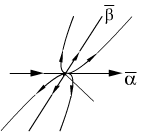
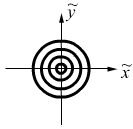
4°. Классификация точек покоя линейных систем 2-го порядка с постоянными коэффициентами.


![]()
![]() ,
где
,
где
 .
.
1.
|
Устойчивый узел.
|
2.
,
|
|
3.
.
|
«седло»
|
4. ![]()
![]()
Утверждение:
![]() -
действ. вектор функц. тогда и только
тогда, когда
-
действ. вектор функц. тогда и только
тогда, когда
![]() .
.

![]()
![]()
![]() ,
,
![]() -
линейно не зависимы.
-
линейно не зависимы.



![]() -
невырожденная матрица.
-
невырожденная матрица.
Оператор хорошо преобразует вектора.
![]() .
.


![]()
семейство окружностей, преобразованных оператором |
семейство эллипсов «центр».
|
5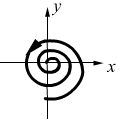 .
.
![]() ,
,
![]() ,
,
![]() .
устойчивый фокус.
.
устойчивый фокус.
![]()
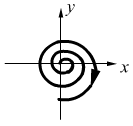
6. ,
,
![]() .
неустойчивый фокус.
.
неустойчивый фокус.
7 О |
8
|
9 О
|
1
0.
|
1 О бщее решение: |
1
2.
|
1
О бщее решение:
|
1
4.
|
Билет № 24
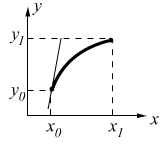
§ 10. Краевая задача для ЛДУ 2-го порядка.
1°.Постановказадачи.
![]()

![]()
![]()
![]()
![]()
Опред.:
Если
![]() ,
то краевые условия называются однородными.
,
то краевые условия называются однородными.
![]()
Опред.:
Если
![]() удовлетворяет краевым условиям, то
удовлетворяет краевым условиям, то
![]() удовлетворяет однородным краевым
условиям.
удовлетворяет однородным краевым
условиям.
![]()
![]()
Пример 1:
|
Пример 2:
|
Билет № 25
2°. Задача Штурма-Лиувилля.
![]()
![]() -
непр.дифф.
-
непр.дифф.
![]() ,
,
![]() -
непрерывны на
-
непрерывны на
![]() ,
,
![]() ,
,
![]() на
,
на
,
![]() .
.
Требуется найти
все значения
![]() (собственное значение) при которых
существует собственная функция
(собственное значение) при которых
существует собственная функция
![]() ,
удовлетворяющая уравнению и краевым
условиям.
,
удовлетворяющая уравнению и краевым
условиям.
Свойства собственного значения и собственной функции.
1.
Существует монотонной возрастающая
последовательность собственных значений
![]() ,
причем
,
причем
![]() соответствует собственная функция
соответствует собственная функция
![]() ,
обращающаяся в ноль ровно
раз на
,
обращающаяся в ноль ровно
раз на
![]() .
.
2. Если
![]() ,
то все собственные значения положительны,
за исключением случая
,
то все собственные значения положительны,
за исключением случая
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.
Собственные функции на отрезке
образуют ортонормированную систему с
весом
,
то есть
![]()
4.
Всякая функция
![]() ,
удовлетворяющая краевым условиям и
имеющая непрерывную 1-ю производную и
кусочно-непрерывную 2-ю производную,
разлагается в абсолютно и равномерно
сходящийся ряд по собственным функциям
:
,
удовлетворяющая краевым условиям и
имеющая непрерывную 1-ю производную и
кусочно-непрерывную 2-ю производную,
разлагается в абсолютно и равномерно
сходящийся ряд по собственным функциям
:
![]() ,
где
,
где
![]() .
.
Пример:
![]()
![]()
![]()
Характеристические
корни:
![]() .
.
1).
![]() ,
,
![]()


![]() .
.
2).
![]()
![]()
![]() .
.
3).
![]()
![]()
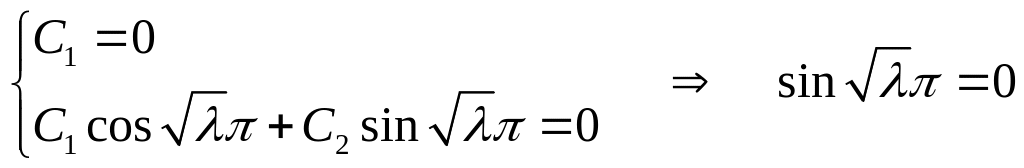 ;
;
![]() ,
,
![]() ;
;
![]()
![]() (
(![]() ,
,
![]() ,
,
![]() )
)
![]() ,
,
![]()
![]()
![]() - орт. на
- орт. на
![]() .
.
Билет № 26
§ 1. Классификация УРЧП.
1°. Определение.
Опред.:
УРЧП – это
у-е
 ,
где
,
где
![]()
 - независимые
переменные,
- независимые
переменные,
![]() .
.
![]()
Примеры у-ий в матфизике:
![]()

![]()
![]()
 ,
,
![]()
![]() .
.
![]()
![]()
2°. Линейные уравнения 2-го порядка от двух независимых переменных.
![]() .
.
Существуют следующие типы таких уравнений:
Гиперболические:
![]()
Параболические:
![]()
Эллиптические:
![]()
3°. Уравнение характеристик.
![]()
![]()
![]()
 ,
,

 - эти семейства
кривых называются характеристическими
кривыми
(или характеристиками).
- эти семейства
кривых называются характеристическими
кривыми
(или характеристиками).
Если сделать замену
переменных
![]() ,
,
![]() ,
и подставить ее в исходное уравнение,
оно существенно упростится.
,
и подставить ее в исходное уравнение,
оно существенно упростится.
![]() .
.
Билет № 27
4°. Приведение к каноническому виду линейных уравнений 2-го порядка от двух независимых переменных.
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Гиперболический тип.
![]()
![]() .
.
Можно считать, что
(так как если
![]() ,
то в исходном уравнении меняются местами
переменные
и
.
Если же
,
то в исходном уравнении меняются местами
переменные
и
.
Если же
![]() ,
то вообще решать нечего).
,
то вообще решать нечего).
Следовательно, , .

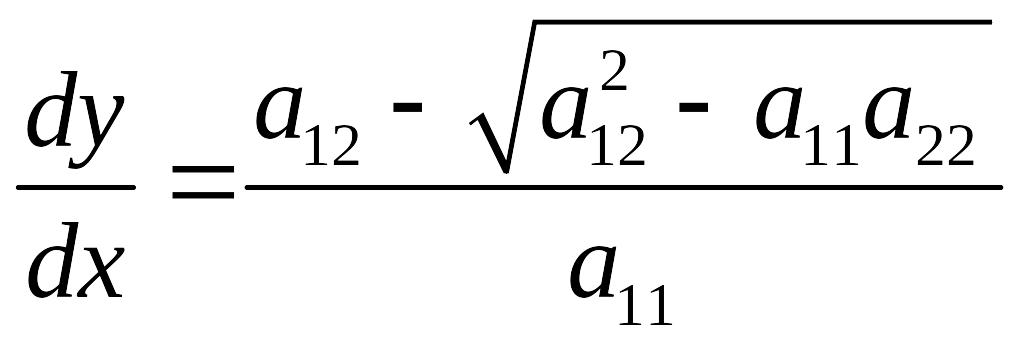
![]()
![]()
![]()
![]() .
.
Билет № 28
4°. Приведение к каноническому виду линейных уравнений 2-го порядка от двух независимых переменных.
,
Параболический тип.
Можно считать,
что
,
![]() .
.
![]()
![]()
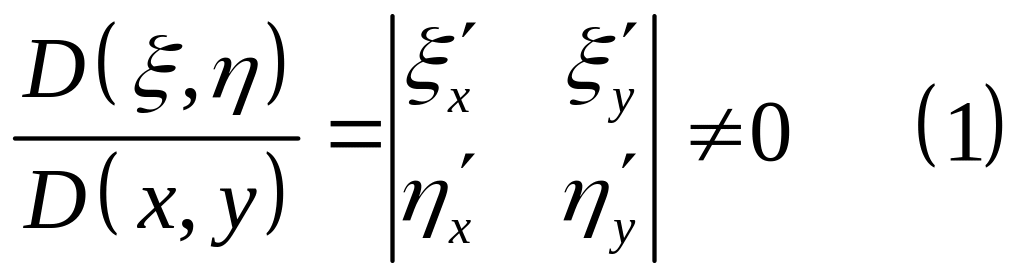
![]()
![]() ,
,
![]()
![]()
![]()
![]()
Эллиптический тип.
Можно считать, что
(так как если
,
то
![]() ,
чего быть не может).
,
чего быть не может).
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
 Следовательно,
Следовательно,
![]() .
.
![]()
![]()
![]() .
.
Билет №29
§ 2. Колебания бесконечной струны.
1°. Постановка задачи.
Опред.: Струна бесконечная - то есть колебания на одном конце струны очень нескоро дойдут до другого конца.
![]()
Н ачальные
условия:
ачальные
условия:
![]()

![]()
Нужно найти положение струны в заданный момент времени в полуплоскости.
2°. Формула Даламбера.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
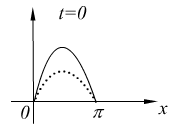
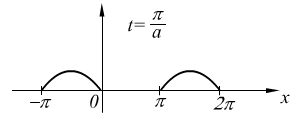
3°. Физический смысл.
![]()
![]()
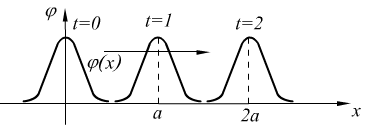

бегущая волна
Билет № 30
§ 3. Начально-краевая задача для уравнения 2-го порядка от двух независимых переменных.
1°. Постановка задачи.
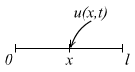
![]()
![]()
Краевые условия:
|
|
2°. Метод Фурье.
![]()
![]()

Если бы
![]() ,
то
,
,
то
,
![]() ,
,
![]()

![]()

![]() ,
,
![]() .
.
![]()
Если функция непрерывна и имеет кусочно-непрерывную производную, то тригонометрический ряд для сходится абсолютно и равномерно к .
Докажем, что
производные
![]() и
и
![]() существуют.
существуют.
 - абсолютно и
равномерно сходятся, так как:
- абсолютно и
равномерно сходятся, так как:

![]() и достаточно
больших
.
и достаточно
больших
.
Билет № 31
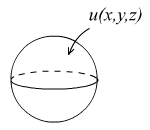
§ 4. Задача Дирихле для уравнения Лапласа.
1°. Постановка задачи для трехмерного тела.
![]()
![]()
2°. Задача Дирихле для круга.
![]()
 ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
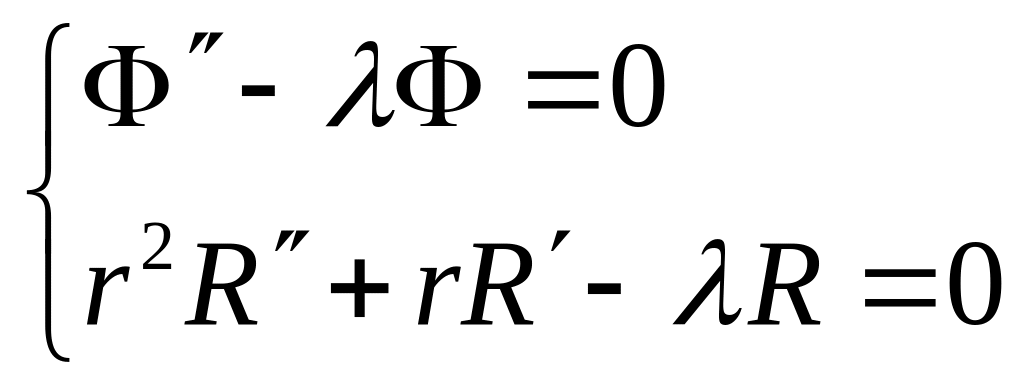
![]()


,
![]()
![]()
Подставляем во второе уравнение , получаем:
![]()
![]()
Получилось уравнение Эйлера.
![]() ,
,
![]()
![]() ,
,
![]()
Если
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() проинтегрировав,
получаем
проинтегрировав,
получаем
![]() (в нуле не определен, поэтому по смыслу
задачи мы должны взять
(в нуле не определен, поэтому по смыслу
задачи мы должны взять
![]() ).
).
Получим:
![]() ,
,
![]() ,
,
![]()
Любая функция этого набора удовлетворяет уравнению Лапласа. Рассматривая сумму этих функций, то есть ряд:
![]() ,
,
![]()
Должно быть
справедливо для всех
![]() .
.
![]() ,
,
![]() ,
,
![]()
Билет № 32
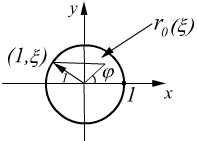
3°. Интегральная функция Пуассона.
![]()
![]()
![]()

(ядро Пуассона)
![]()
![]() {представим
как сумму геометрической прогрессии}
{представим
как сумму геометрической прогрессии}
![]()
 .
.
![]() .
.
![]() .
.
4°. Формула Пуассона для шара.
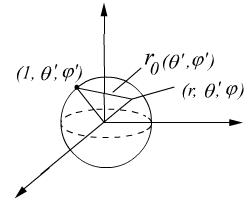
![]() .
.
Билет № 33
§ 5. Колебания закрепленной струны.
1°. Постановка задачи.
Уравнение колебаний струны:
Граничные условия:
|
Начальные условия:
|
2°. Метод Фурье.
![]()
![]()
![]()
![]()
Задача Лиувилля:
 ,
,
![]()
![]()
![]()
![]()
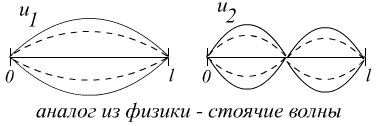
![]()
![]()
![]()
![]()
![]()
![]()
Билет № 34
§ 6. Вывод уравнений математической физики.
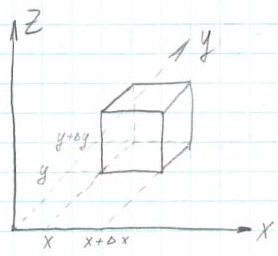
1°. Уравнение теплопроводности.
|
Количество тепла, проходящее через
левую грань куба справа налево за
интервал времени (t,∆t+t),
равно
Общее количество тепла, входящее в Q, за интервал времени (t,t+∆t)
,
|
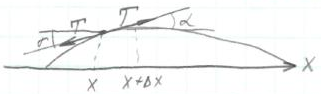
2°. Уравнения малых колебаний струны.
|
|
![]() (x+∆x,t)-
(x+∆x,t)-![]() (x,t))=T
(x,t))=T![]() (x,t)∆x
(x,t)∆x
𝜌∆x (x,t)=T (x,t)∆x
![]()

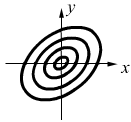


 .
.


 бщее
решение:
бщее
решение: 
 .
.





 .
.



 бщее
решение:
бщее
решение:





 1.
1.



 3.
3.