
- •Билет № 1
- •1°. Пример
- •2°. Определения.
- •3 °. Геометрический смысл ду.
- •4°. Задача Коши.
- •1°. Уравнение в полных дифференциалах.
- •2°. Принцип сжатых отображений.
- •3°. Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.
- •3°. Связь нормальных систем с общими дифференциальными уравнениями (оду) n-го порядка.
- •5°. Нормальная линейная система (нлс).
- •1°. Линейная однородная система (лос).
- •2°. Фундаментальная система решений (фср).
- •Фундаментальная матрица однородной системы и её свойства. Определитель Вронского.
- •3°. Определитель Вронского (Вронскиниан).
- •5°. Линейные однородные дифференциальные уравнения -го порядка.
- •Свойства уравнения :
- •4°. Линейные неоднородные уравнения - го порядка с постоянными коэффициентами и правой частью.
- •5°. Лос с постоянными коэффициентами.
- •5°. Лос с постоянными коэффициентами.
- •1°. Теорема о непрерывной зависимости решений от реальных условий.
- •2°. Устойчивость по Ляпунову. Асимптотическая устойчивость.
- •3°. Теорема Ляпунова.
- •4°. Классификация точек покоя линейных систем 2-го порядка с постоянными коэффициентами.
4°. Линейные неоднородные уравнения - го порядка с постоянными коэффициентами и правой частью.
![]()
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]()
![]() ,
где
,
где
![]() ,
,
![]() .
.
![]() ,
,
![]()
Теорема:
Если
![]() -
корень кратности
-
корень кратности
![]() характеристического многочлена
,
то частное решение уравнения
характеристического многочлена
,
то частное решение уравнения
![]() можно искать в виде
можно искать в виде
![]() ,
где
,
где
![]() ,
,
![]() .
.
Доказательство:
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Билет № 19
5°. Лос с постоянными коэффициентами.

![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() - собственный
вектор
- собственный
вектор
![]() с собственным числом
с собственным числом
![]() .
.
![]()
![]()
![]() -
корни характеристического многочлена.
-
корни характеристического многочлена.
![]() -
собственные вектора.
-
собственные вектора.
Опред.: Если собственные числа различны, то соответствующие им собственные вектора линейно-независимы.
Опред.: Линейный оператор (матрица) называется диагонализируемым, если она имеет линейно-независимых собственных векторов.
Опред.:
Если
-
линейно независимы, то
![]() - ФСР.
- ФСР.
Билет № 20
5°. Лос с постоянными коэффициентами.
Опред.: Если матрица не диагонализируемая, то ее характеристическое уравнение имеет кратные корни.
![]()
Лемма:
Пусть
-
фундаментальная матрица ЛОС
,
где
![]() -
матрица
-
матрица
![]() ,
а
,
а
![]() -
невырожденная матрица. Тогда
-
невырожденная матрица. Тогда
![]() .
.
ЛОС
![]() ,
где
,
где
![]()
Доказательство:
![]()
![]()
Следствие 1:
|
|
Вывод: собственные числа увеличатся на .
Следствие 2:
- постоянная матрица.
![]()
Вывод: собственные числа не изменятся.
Теорема (о структуре общего решения):
Фундаментальную
систему решений линейной однородной
системы
можно составить из
подмножеств, соответствующих попарно
различным корням
![]() характеристического многочлена, причем
корню
кратности
соответствует
линейно независ. решений вида
характеристического многочлена, причем
корню
кратности
соответствует
линейно независ. решений вида
 ,
где
,
где
![]() -
многочлены степени не превосходящей
-
многочлены степени не превосходящей
![]() .
.
Доказательство:
Доказательство проводим индукцией по при фиксированном .
База индукции
при
![]() все корни (собственные числа) различны
теорема справедлива.
все корни (собственные числа) различны
теорема справедлива.
Шаг индукции.
Предположим,
что теорема справедлива для числа
![]() .
Докажем ее для
.
.
Докажем ее для
.
Без ограничения
общности можно считать, что
![]() ,
,
![]() ,
а теорема уже доказана для случая, когда
-
корень кратности
,
,
а теорема уже доказана для случая, когда
-
корень кратности
,
![]() -корень
кратности
-корень
кратности
![]() ,
,
![]() -корень
кратности
-корень
кратности
![]() .
.
Можно считать, что
![]() ,
иначе делаем замену
,
иначе делаем замену
![]() на
на
![]() .
.
Пусть
![]() - собственный вектор, соответствующий
.
Значит,
- собственный вектор, соответствующий
.
Значит,
 .
Можно считать, что
.
Можно считать, что
![]() .
.
Сделаем замену
переменных:
![]() ,
,
 ,
,


 .
.
,

Из уравнения
![]() следует:
следует:

![]()

учитывая, что
![]() ,
получаем:
,
получаем:
![]() .
.
ФСР
:
|
|
ФСР
|
В данной матрице
|
![]() ,
,
![]() (где
-
фундаментальная матрица исходной
системы).
(где
-
фундаментальная матрица исходной
системы).
|
В результате такого произведения получим матрицу, аналогичную матрице . |
Билет № 21
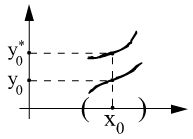
1°. Теорема о непрерывной зависимости решений от реальных условий.
![]()
![]()
![]()
![]()
![]()
Опред.:
Решение
называется непрерывно зависящим от
начальных условий на интервале
![]() :
:
![]()
![]()
![]()
![]()
Теорема:
Если
непрерывна на
,
![]() на
,
то
ур-я
на
,
то
ур-я
![]() ,
непрерывно зависит от начальных условий
на интервале
,
где
,
непрерывно зависит от начальных условий
на интервале
,
где
![]() ,
.
,
.
Доказательство:


![]()
![]()

![]()




 .
. - степень
- степень

