
- •1. Элементы теории множеств
- •1.1 Понятие множества. Основные определения
- •Способы задания множества
- •Равенство множеств
- •Подмножество
- •Операции над множествами
- •Предварительные замечания
- •Объединение множеств
- •1.5.3 Пересечение множеств
- •1.5.4 Разность множеств
- •1.5.5 Симметрическая разность
- •1.5.6 Универсальное множество
- •1.5.7 Дополнение множества
- •Принцип двойственности в алгебре множеств
- •Тождества алгебры множеств
- •Разбиение множества
- •Упорядочение элементов и прямое произведение множеств
- •Упорядоченное множество
- •Прямое произведение множеств
- •1.9.3 Проекция множества
- •1.10 Соответствия
- •1.10.1 Обратное соответствие
- •1.10.2 Композиция соответствий
- •1.10.3 Отображения и функции
- •1.10.4 Основные свойства отображений
- •1.11 Функция
- •1.11.1 Способы задания функции
- •1.11.2 Сужение функции
- •1.11.3 Обратная функция
- •1.11.4 Функция времени
- •1.11.5 Понятие функционала
- •1.11.6 Понятие оператора
- •1.12 Отношения
- •1.12.1 Задание бинарных отношений
- •Свойства отношений
- •1.12.3 Отношение эквивалентности
- •1.12.4 Отношение порядка
- •1.13 Конечные и бесконечные множества
- •1.13.1 Счётные и несчётные множества
- •1.13.2 Свойства счетных множеств
- •1. Всякое подмножество счетного множества конечно или счетно.
- •2. Объединение любого конечного или счетного множества счетных множеств есть снова счетное множество.
- •3. Всякое бесконечное множество содержит счетное подмножество.
- •1.13.3 Эквивалентность множеств
- •1.13.4 Теорема г. Кантора
- •1.13.5 Теорема Кантора – Бернштейна
- •1.13.6 Верхняя и нижняя границы множества
- •1.13.7 Теорема о верхних и нижних границах подмножества
- •1.13.8 Понятие мощности множества
- •2. Основные положения теории графов
- •2.1 Определение графа
- •2.2 Матричные представления графа
- •2.3. Достижимость
- •2.4. Неориентированные графы
- •2.5. Изоморфизм графов
- •2.6. Отношение порядка и отношение эквивалентности на графе
- •2.7. Характеристики графов
- •2.8 Операции над графами
- •2.9. Определение путей экстремальной длины
- •2.9.1. Задача о кратчайшем пути между двумя вершинами (ориентированного графа
- •2.9.2 Задача о нахождении пути максимальной длины между двумя фиксированными вершинами ориентированного графа
- •Номера работ обозначены числами в кружке.
- •Литература
1.5.4 Разность множеств
Разностью множеств А и В называют множество, состоящее из тех и только тех элементов, которые принадлежат только множеству А и не принадлежат множеству В. Разность множеств1 А и В обозначается А\В. Формально определение разности множеств А и В можно записать в виде:
![]() .
1.16
.
1.16
Примеры.
Пусть имеем А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда А\В={4,8,16}, а B\A={1,2,7,17,30}.
A={a,b,c,d}; B={a,d,e,f,g}. В этом случае получаем: А\В={b,c} и B\A={e,f,g}.
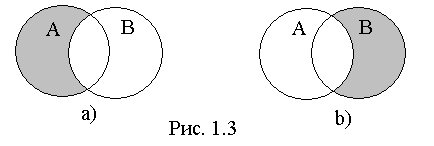 Если как и ранее
множества А и В изобразить в виде точек
кругов А и В соответственно, то разность
множеств будет представляться так, как
это показано на рис. 1.3, где а) соответствует
разности А\В, b)- разности
B\A.
Если как и ранее
множества А и В изобразить в виде точек
кругов А и В соответственно, то разность
множеств будет представляться так, как
это показано на рис. 1.3, где а) соответствует
разности А\В, b)- разности
B\A.
1.5.5 Симметрическая разность
Симметрической разностью множеств А и В называют множество, состоящее из объединения множеств разностей А\В и В\А. Симметрическая разность множеств А и В обозначается символом , т.е А В. Таким образом, по определению
![]() .
1.17
.
1.17
Нетрудно
убедиться, что
![]() .
1.18
.
1.18
Примеры.
Имеем: А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда
А В={1,2,4,7,8,16, 17,30}.
A={a,b,c,d}; B={a,d,e,f,g}. В этом случае получаем А В={b,c,e,f,g}.
Графически симметричная разность множеств А и В может быть представлена как показано на рис. 1.4. Закрашенные области соответствуют симметрической разности множеств А и В.

1.5.6 Универсальное множество
Если в некотором рассмотрении участвуют только подмножества некоторого фиксированного множеств I, то это самое большое множество называют универсальным (или полным) множеством.
В различных конкретных случаях роль универсального множества играют различные множества. Так, при рассмотрении студентов института универсальным (полным) множеством является вся совокупность студентов. Отдельные группы (факультеты) можно рассматривать как подмножества. В некоторых случаях универсальным множеством может являться и отдельная группа, в которой имеют место свои подмножества (отличники; студенты, проживающие в общежитии; юноши; девушки и т.п.).
Вполне очевидно, что для универсального множества справедливы следующие соотношения:
![]() и
и
![]() 1.19
1.19
Универсальное множество удобно изображать графически в виде множества точек прямоугольника. Различные области внутри прямоугольника будут означать различные подмножества универсального множества. Изображение множества в виде областей в прямоугольнике, представляющем универсальное множество, называют диаграммой Эйлера-Венна.
1.5.7 Дополнение множества
Множество
![]() ,
определяемое из соотношения
,
определяемое из соотношения
![]() 1.20
1.20
называют дополнением множества А (до универсального множества I)
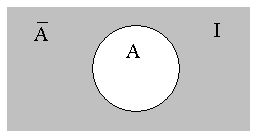
Графически дополнение множества А может быть представлено как показано на рис. 1.5.
Формальное определение дополнения множества А может быть записано как
![]() 1.21
1.21
Из
определения дополнения множества
следует, что А и
![]() не имеют общих элементов, т.е.
не имеют общих элементов, т.е.
![]() 1.22
1.22
 Кроме
того,
Кроме
того,
![]() 1.23
1.23
Из
симметрии формул 1.22 и 1.23 следует, что
не только
является
дополнением А, но и А является дополнением
.
Но дополнение
есть
![]() .
Таким образом
.
Таким образом
![]() 1.24
1.24
Рис. 1.5
С помощью операции дополнения удобно представить разность множеств:
![]() =
=![]() ,
т.е
,
т.е
![]() 1.25
1.25
