2. Объединение множеств

Объединением множеств А и В называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В. Объединение множеств А и В обозначается символом , т.е. .

Определение объединения множеств можно записать как

1.6

Объединение множеств иногда называют суммой множеств и обозначают А+В. Однако свойства объединения множеств несколько отличаются от свойств суммы при обычном арифметическом понимании. Поэтому термином сумма пользоваться не рекомендуется.

Примеры.

1. Пусть А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда

={1,2,4,5,7,8,12,16,17, 21,30}.

2. Пусть A={a,b,c,d}; B={a,d,e,f,g}. Тогда ={a,b,c,d,e,f,g}.

Е сли множества А и В представить в виде точек, ограниченных окружностями А и В соответственно, то объединение множеств представляет собой закрашенную область, ограниченную обоими кругами, как это показано на рис. 1.1.

Понятие объединения множеств можно распространить и на большее число множеств. Пусть М={X₁, X₂,…. X_n} – совокупность n множеств X₁, X₂, … X_n, называемую системой множеств. Объединение этих множеств представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств системы М.

1.7

Для объединения множеств справедливы коммутативный и ассоциативный законы:

; 1.8

. 1.9

Вполне очевидно, что . 1.10

1.5.3 Пересечение множеств

Пересечением множеств А и В называют множество, состоящее только их тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. Пересечение множеств обозначается символом , т.е. . Определение пересечения может быть записано как

1.11

Пересечение множеств иногда называют произведением множеств, что некорректно.

Примеры.

1. Если А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}, то 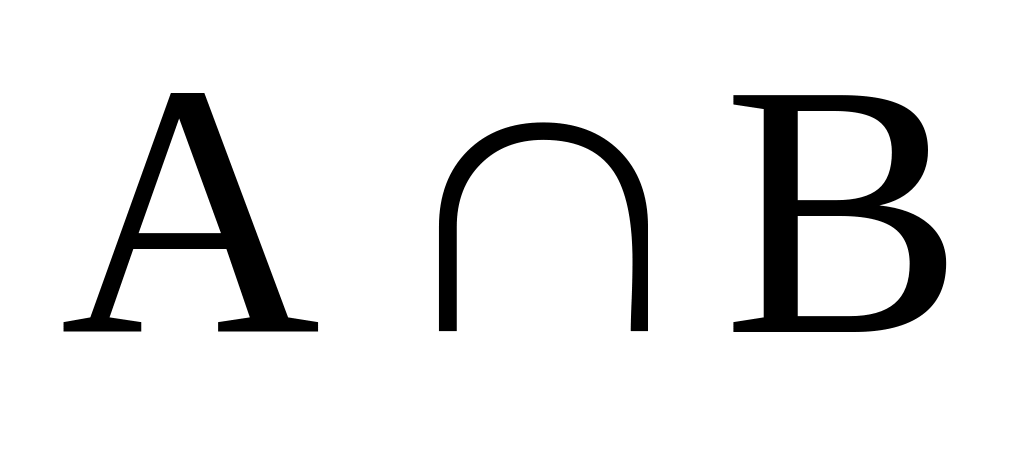={5,12,21}.

2. Если A={a,b,c,d}; B={a,d,e,f,g}, то ={a,d}.

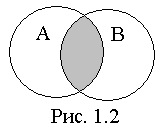Если А – множество левого круга, В – множество правого круга, то пересечение множеств представляет собой закрашенную область, являющуюся общей частью обоих кругов, как это показано на рис. 1.2.

Множества А и В называются непересекающимися, если они не имеют общих элементов, т.е. =.

Пример. Пусть А={3,4,5}, B={2,6,7}. Тогда =.

Множества А и В находятся в общем положении, если выполняются три условия:

• Существует элемент множества А, не принадлежавший множеству В;

• Существует элемент множества В, не принадлежавший множеству А;

• Существует элемент, принадлежащий как множеству А, так и множеству В.

Пересечение распространяется и на большее количество множеств. Пусть имеем систему множеств М={X₁, X₂,…. X_n}. Множество

1.12

представляет собой множество, элементы которого принадлежат каждому из множеств системы М.

Пересечение множеств обладает свойством коммутативности

1.13

и ассоциативности

1.14

Кроме того имеет место соотношение: . 1.15