
- •1. Элементы теории множеств
- •1.1 Понятие множества. Основные определения
- •Способы задания множества
- •Равенство множеств
- •Подмножество
- •Операции над множествами
- •Предварительные замечания
- •Объединение множеств
- •1.5.3 Пересечение множеств
- •1.5.4 Разность множеств
- •1.5.5 Симметрическая разность
- •1.5.6 Универсальное множество
- •1.5.7 Дополнение множества
- •Принцип двойственности в алгебре множеств
- •Тождества алгебры множеств
- •Разбиение множества
- •Упорядочение элементов и прямое произведение множеств
- •Упорядоченное множество
- •Прямое произведение множеств
- •1.9.3 Проекция множества
- •1.10 Соответствия
- •1.10.1 Обратное соответствие
- •1.10.2 Композиция соответствий
- •1.10.3 Отображения и функции
- •1.10.4 Основные свойства отображений
- •1.11 Функция
- •1.11.1 Способы задания функции
- •1.11.2 Сужение функции
- •1.11.3 Обратная функция
- •1.11.4 Функция времени
- •1.11.5 Понятие функционала
- •1.11.6 Понятие оператора
- •1.12 Отношения
- •1.12.1 Задание бинарных отношений
- •Свойства отношений
- •1.12.3 Отношение эквивалентности
- •1.12.4 Отношение порядка
- •1.13 Конечные и бесконечные множества
- •1.13.1 Счётные и несчётные множества
- •1.13.2 Свойства счетных множеств
- •1. Всякое подмножество счетного множества конечно или счетно.
- •2. Объединение любого конечного или счетного множества счетных множеств есть снова счетное множество.
- •3. Всякое бесконечное множество содержит счетное подмножество.
- •1.13.3 Эквивалентность множеств
- •1.13.4 Теорема г. Кантора
- •1.13.5 Теорема Кантора – Бернштейна
- •1.13.6 Верхняя и нижняя границы множества
- •1.13.7 Теорема о верхних и нижних границах подмножества
- •1.13.8 Понятие мощности множества
- •2. Основные положения теории графов
- •2.1 Определение графа
- •2.2 Матричные представления графа
- •2.3. Достижимость
- •2.4. Неориентированные графы
- •2.5. Изоморфизм графов
- •2.6. Отношение порядка и отношение эквивалентности на графе
- •2.7. Характеристики графов
- •2.8 Операции над графами
- •2.9. Определение путей экстремальной длины
- •2.9.1. Задача о кратчайшем пути между двумя вершинами (ориентированного графа
- •2.9.2 Задача о нахождении пути максимальной длины между двумя фиксированными вершинами ориентированного графа
- •Номера работ обозначены числами в кружке.
- •Литература
2.2 Матричные представления графа
Одной из форм математического представления графа является его представление в виде матриц смежности инциденций.
Вершины х и y являются смежными, если они различны и если существует дуга, идущая из х в y.
Дугу u называют инцидентной вершине х, если она заходит в эту вершину или исходит из нее.
Обозначим через х1, х2, …, хn вершины графа, а через u1, u2, …, um его дуги.
Матрицей смежности
R=![]() графа G=(Х,
Г) называется квадратная матрица порядка
n
(n
– число вершин графа), элементы которой
ri,j
(i=1,
2, …n;
j=1,2,
…n)
определяются следующим образом:
графа G=(Х,
Г) называется квадратная матрица порядка
n
(n
– число вершин графа), элементы которой
ri,j
(i=1,
2, …n;
j=1,2,
…n)
определяются следующим образом:
![]() 2.6
2.6
Матрица смежности
полностью определяет структуру графа.
Возведем матрицу смежности в квадрат.
Элемент
![]() матрицы R2
определяется по формуле:
матрицы R2
определяется по формуле:
![]() 2.7
2.7
Слагаемое
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() и
и
![]() ,
в противном случае слагаемое
,
в противном случае слагаемое
![]() .
Так как из равенства
.
Так как из равенства
![]() следует существование пути длины два
(пути, проходящего через две дуги) из
вершины хi
в вершину
xj,
проходящего через вершину xk,
то
равно числу путей длины два, идущих из
xi
в xj
через xk.
следует существование пути длины два
(пути, проходящего через две дуги) из
вершины хi
в вершину
xj,
проходящего через вершину xk,
то
равно числу путей длины два, идущих из
xi
в xj
через xk.
Если
![]() является элементом матрицы
является элементом матрицы
![]() ,
то
0
равно числу путей длины p,
идущих из xi
в xj.
,
то
0
равно числу путей длины p,
идущих из xi
в xj.
Пример. На рис. 2.4 задан граф G. построить матрицу смежности и выяснить, сколько путей длины три существует в графе G.
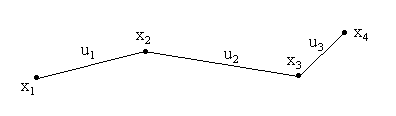
Рис. 2.4
Решение.
![]()
![]()
![]()
![]()
Элемент
![]() ,
следовательно в данном графе существует
единственный путь длиной три – это путь
из вершины х1
в вершину х4:
х1 u1
x2
u2
x3
u3
x4.
,
следовательно в данном графе существует
единственный путь длиной три – это путь
из вершины х1
в вершину х4:
х1 u1
x2
u2
x3
u3
x4.
Все элементы
матрицы
![]() равны нулю. Следовательно, в графе
отсутствуют пути длиной четыре.
равны нулю. Следовательно, в графе
отсутствуют пути длиной четыре.
Матрицей инциденций
![]() называется прямоугольная матрица
размерности nm
(n-число
вершин, m
– число дуг), элементы которой
называется прямоугольная матрица
размерности nm
(n-число
вершин, m
– число дуг), элементы которой
![]()
![]() определяются следующим образом:
определяются следующим образом:
![]() 2.8
2.8
Если граф G не содержит петель, то каждый столбец матрицы S содержит единственный элемент, равный 1 (дуга имеет начало) и единственный элемент, равный –1 (дуга имеет конец), а остальные элементы равны нулю.
Пример. Построить матрицу смежности и матрицу инциденций для графа, приведенного на рис. 2.5.
Решение. Матрица
смежности будет иметь вид:
xi
x1
x2
x3
x4
x5
x1
0
1
0
1
0
x2
0
0
1
1
0
x3
0
0
0
0
0
x4
0
1
1
0
1
x5
1
0
1
0
0
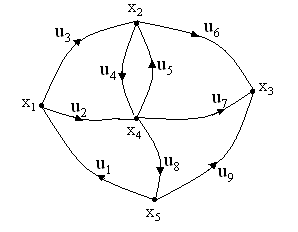 Рис.
2.5
Рис.
2.5
Матрица инциденций будет иметь вид:
-
xi /uj
u1
u2
u3
u4
u5
u6
u7
u8
u9
x1
-1
1
1
0
0
0
0
0
0
x2
0
0
-1
1
-1
1
0
0
0
x3
0
0
0
0
0
-1
-1
0
1
x4
0
-1
0
-1
1
0
1
1
0
x5
1
0
0
0
0
0
0
-1
1
Или в более компактной форме матрица смежности R и инциденций S будут иметь вид:
![]() ;
;
![]() .
.
