§ 2. Линейные нормальные системы с постоянными коэффициентами

1. Линейные нормальные однородные системы с постоянными коэффициентами. Рассмотрим систему

, (1)

где постоянная матрица. Опишем методы интегрирования системы (1).

1⁰. Метод Эйлера. Решение системы (1) ищут в виде

где искомые постоянные числа, причем хотя бы одно число , . Подставляя в систему (1) и сокращая на получаем систему ЛОАУ с неизвестными .

(2)

Для того, чтобы она имела нетривиальное решение, необходимо и достаточно, чтобы ее детерминант не был равен нулю:

. (3)

Равенство (3) называют характеристическим уравнением системы (1). Находя из (3), для каждого из находим соответствующий собственный вектор матрицы , определенный системой (2).

Рассмотрим следующие случаи:

а) Корни характеристического уравнения действительные и различны. Тогда матрица имеет линейно независимых собственных векторов , где . Тогда решением системы будут вектор-функции .

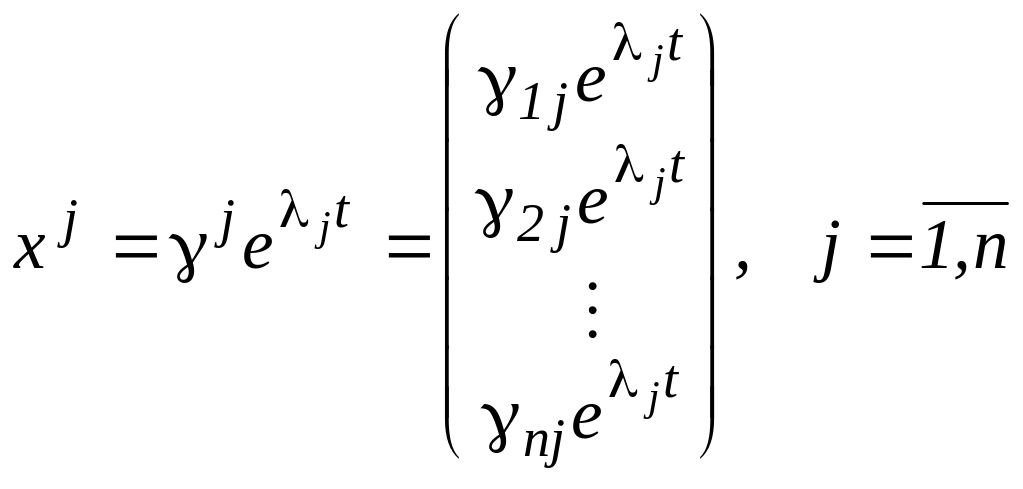Функции линейно независимы, значит, образуют базис решений системы (1). Действительно, для матрицы

имеем , так как его столбцы – линейно независимые собственные векторы.

Таким образом, общее решение системы линейных однородных уравнений с постоянными коэффициентами в случае действительных различных корней характеристического уравнения имеет вид

.

б) Корни характеристического уравнения комплексные, а именно паре комплексно сопряженных корней характеристического уравнения соответствует пара действительных решений

, .

Общее решение системы (1) в этом случае .

в) Среди корней характеристического уравнения есть кратные. Если есть характеристическое число кратности , то ему соответствуют решения вида

, (4)

где – полиномы от степени не выше, чем , которые в совокупности имеют произвольных коэффициентов, причем все остальные коэффициенты этих полиномов выражаются через эти произвольных коэффициента.

На практике при нахождении решения, соответствующего характеристическому числу , полиномы считают полинмами ( ) степени с неопределенными коэффициентами. Подставляя (4) в (1) и сравнивая коэффициенты при одинаковых степенях слева и справа, необходимо выразить все коэффициенты через из них, которые остаются произвольными.

Все полученные таким образом линейно независимые решения в свокупности образуют ФСР. Тогда общее решение системы имеет вид .

2⁰. Решение с помощью матриц. Решение строится, используя понятие жордановой нормальной формы матрицы.

Набор векторов называют жордановой цепочкой матрицы , если

.

Вектор – собственный, векторы называются присоединенными.

Теорема о структуре решения системы (1). Для произвольной квадратной матрицы порядка существует базис , состоящий из жордановых цепочек , ,..., , соответствующих собственным значениям матрицы . Причем, для каждой такой цепочки существует система решений, так что решения системы (1) записываются

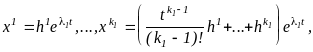
(5)

При этом формула

, (6)

где – константы, всегда дает решение системы (1) и каждое решение системы (1) описывается формулой (6).

2. Линейные неоднородные системы. Рассмотрим линейную неоднородную систему

, (7)

где – вектор-функция с непрерывными на компонентами, и определены.

Теорема (о структуре общего решения линейной неоднородной системы дифференциальных уравнений). Общее решение системы (7) имеет вид , где – ФСР соответствующей однородной системы, некоторое частное решение системы (7).

Для системы имеет место принцип суперпозиций частных решений.

Систему линейных неоднородных уравнений можно решать:

1) методом исключения путем приведения ее к одному уравнению -го порядка,

2) методом вариации произвольных постоянных. Пусть базис решений системы известен и – есть общее ее решение, =col( ).

Заменим на , продифференцируем и подставим и в (7). Получим или, с учетом, что – фундаментальная матрица соответствующей однородной системы, Отсюда ( – будет сущствовать, так как ). Будем иметь ,

Тогда общее решение системы (1)

(8)

3) Метод неопределенных коэффициентов. Если то частное решение неоднородной системы (7) находят по правилам, определенным следующей теоремой.

Теорема. Частное решение системы где -векторный полином степени комплексное число, имеет вид причем векторный полином с компонентами степени, не большей, чем , а число совпадает с кратностью в характеристическом уравнении.

Неизвестные коэффициенты полиномов (компонент ) определяются путем подстановки и сравнения коэффициентов подобных членов, а действительные решения выделяются так же, как и в методе Эйлера.

4) Построение интегрируемых комбинаций. Метод Даламбера. Рассмотрим этот метод в случае системы двух уравнений Умножая второе уравнение системы на чило и складывая с первым уравнением, получим

.

Перепишем последнее уравнение в виде ( )

. (9)

Выберем так, чтобы . Тогда (9) приведется к линейному относительно виду

,

интегрируя которое, получим

. (10)

Если уравнение имеет разные действительные корни и , то из (10) получим два независимых первых интеграла данной системы, значит, интегрирование будет закончено.