6.2.2. Сечение цилиндра плоскостью
При сечении цилиндра плоскостью образуются следующие линии (рис. 6.71 а, б): окружность, если секущая плоскость перпендикулярна оси цилиндра (β); эллипс, если секущая плоскость наклонная (α); прямые линии, если секущая плоскость параллельна образующим цилиндра (γ).
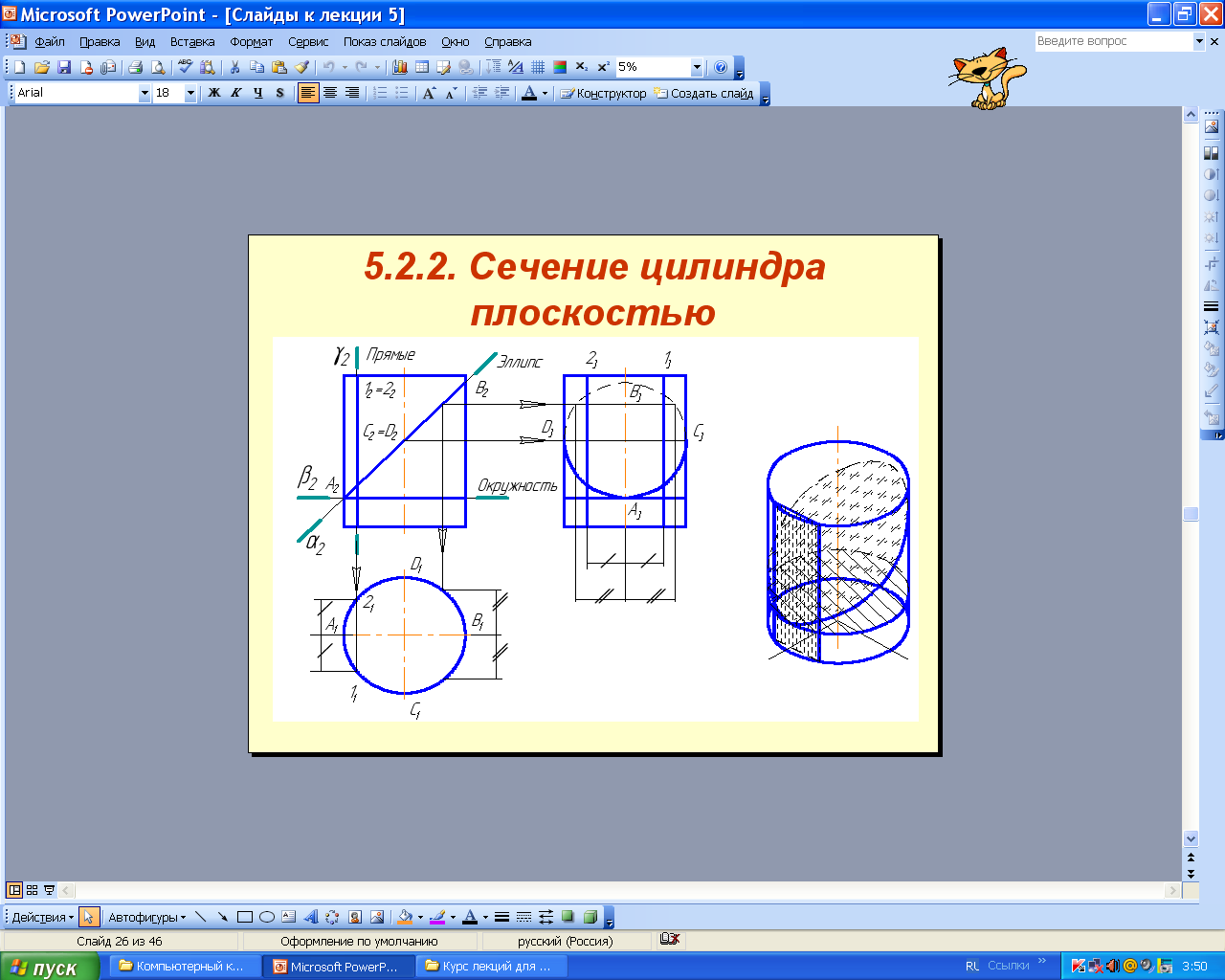
а б
Рис. 6.71
6.2.3. Построение развертки наклонного цилиндра (наклонной призмы) способом раскатки
Рис. 6.72 Анимации\Рис. 6.72.exe
Построение развертки боковой поверхности наклонного цилиндра (наклонной призмы) способом раскатки возможно тогда, когда образующие цилиндра (ребра призмы) являются прямыми уровня. Сущность способа раскатки состоит в том, что участки боковой поверхности между образующими цилиндра (ребрами призмы) совмещают с плоскостью проекций (рис. 6.73). Основание цилиндра разделяют на равные промежутки (вписывают в основание многоугольник), через точки деления проводят образующие (1,2,3, ..,6). В приведенном примере образующие цилиндра являются фронталями. От конечных точек натуральной величины образующих к ним проведены перпендикуляры, на которых циркулем сделаны засечки, равные размеру хорды окружности основания (точки 4,3,2,1,8,7,6,5). Полученные точки обводят кривой линией (или для призмы соединяют отрезками прямых). Таким образом, развертка боковой поверхнос- ти наклонного цилиндра выполняется как развертка вписанной в него наклонной призмы.
Рис. 6.73 Анимации\Рис. 6.73.exe
6.2.4. Сечение шара плоскостью
В сечении шара плоскостью всегда образуется окружность, которая может проецироваться в линию, эллипс или окружность.
На рис. 6.74 построено сечение шара фронтально-проецирующей плоскостью . На фронтальной проекции сечение проецируется в линию, на горизонтальной проекции оно проецируется в виде эллипса, для построения которого достаточно построить характерные точки сечения: высшую и низшую точки (1 и 2), крайние левую и правую (3 и 4), точки видимости (5 и 6). На фронтальной проекции отмечают точки 12 и 22 пересечения плоскости с очерком шара. По линиям связи эти точки переносят на горизонтальную проекцию (11 и 21). Для построения проекций точек 3 и 4 к секущей плоскости проводят плоскость симметрии сечения y, которая пересекает плоскость по линии 3-4 (32=42). Для построения горизонтальных проекций этих точек через точки 32 и 42 проводят вспомогательную плоскость (2), которая пересекает шар по окружности радиусом R. Точки 5 и 6, определяющие границу видимости линии сечения на горизонтальной проекции, лежат на очерковой окружности. Натуральная величина линии сечения равна окружности радиусом 1232.
Рис. 6.74 Анимации\Рис. 6.74.exe