
- •14.8. Основные теоремы дифференциального исчисления
- •14.8. 1. Теорема Ферма (1601-1665гг)
- •Предположим, что т.Е. То будем иметь:
- •Геометрический смысл теоремы Ферма
- •14.8.2. Теорема м. Ролля (1652-1719)
- •Геометрический смысл теоремы Ролля
- •14.8.3. Теорема Лагранжа (1736-1813)
- •Геометрический смысл теоремы Лагранжа
- •14.8.4. Теорема Коши (1789-1857)
- •14.8.5. Правило Лопиталя (1661-1704)
- •Лекция 15. Применение дифференциального исчисления к исследованию функции
- •15.1. Признаки монотонности функции
- •15.2. Экстремумы функции
- •Необходимый признак экстремума функции
- •15.4. Применение второй производной к исследованию функции Второй достаточный признак экстремума.
- •15.5. Выпуклость и вогнутость линии. Точки перегиба
- •15.6. Асимптоты линий
- •15.7. Общая схема исследования функции
- •5. Алгоритм исследования функции на выпуклость и точки перегиба.
- •6. Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке .
- •7. Алгоритм отыскания асимптоты графика функции .
- •8. Алгоритм исследования и построения графика функции.
15.6. Асимптоты линий
Определение
15.5.
Прямая
линия
![]() называется асимптотой,
,
если расстояние от точки линии
до прямой
стремится к нулю при
называется асимптотой,
,
если расстояние от точки линии
до прямой
стремится к нулю при
![]() .
Будем различать вертикальные
и
наклонные
асимптоты.
.
Будем различать вертикальные
и
наклонные
асимптоты.
1) Вертикальные асимптоты графика функции находятся так,
если
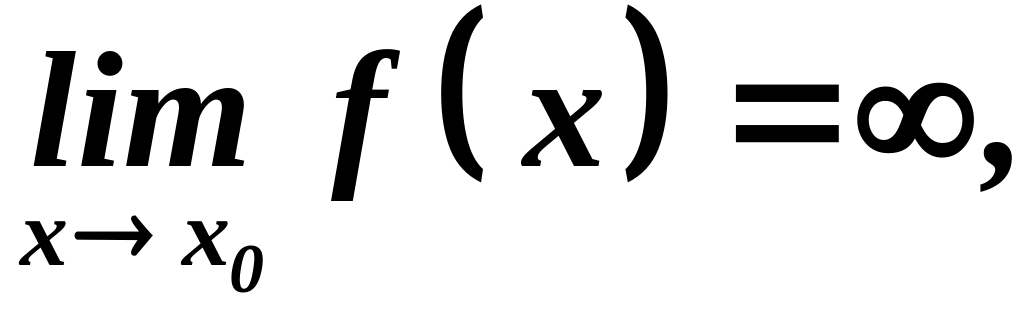 то
то
![]() - вертикальные асимптоты. (Функция,
стремящаяся к
- вертикальные асимптоты. (Функция,
стремящаяся к
![]() исследуется в окрестности точки
,
т.е.
исследуется в окрестности точки
,
т.е.
![]() или
или
![]() ).
).
2) Наклонные асимптоты.
Асимптота
– это прямая, следовательно, ее уравнение
![]() ,
где
,
где
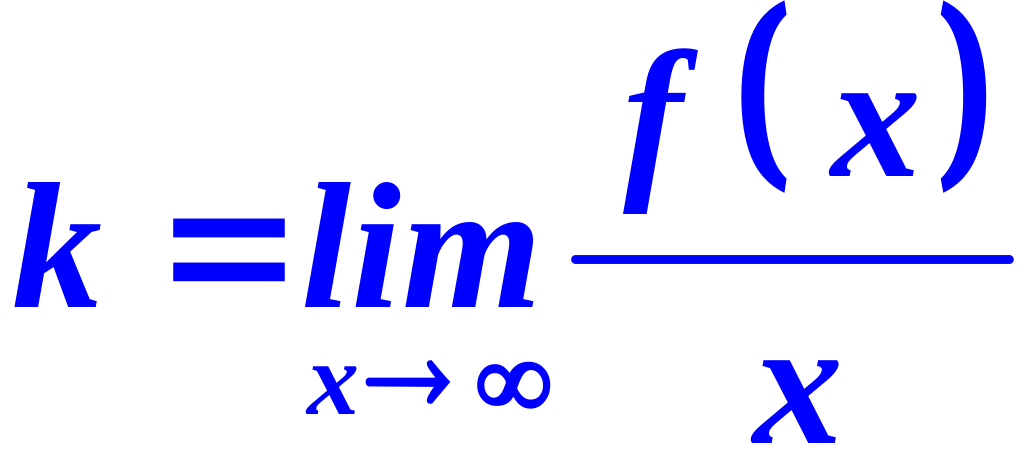 ,
(15.1)
,
(15.1)
 ,
(15.2)
,
(15.2)
Заметим,
что если равенство (15.1)
может осуществляться, а равенство (15.2)
нет
![]() ,
тогда линия
- асимптот не имеет.
,
тогда линия
- асимптот не имеет.
Пример
15.6 .Дана
функция
![]() .
Найти асимптоты.
.
Найти асимптоты.
Вертикальная
асимптота:
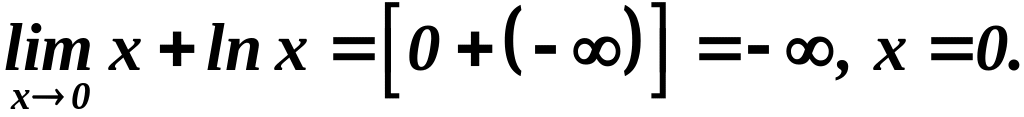
Наклонные
асимптоты:
:
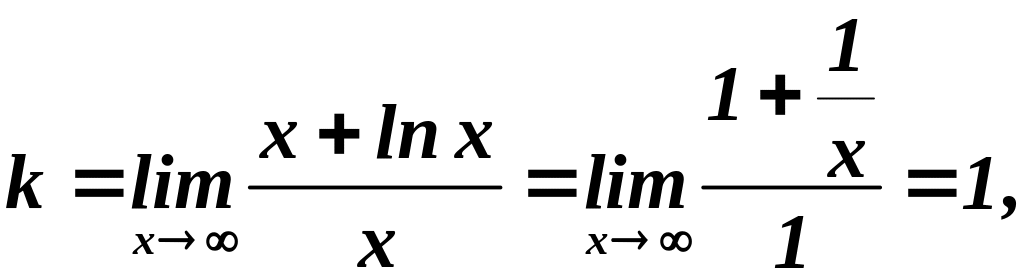
 Наклонных
асимптот нет.
Наклонных
асимптот нет.
Пример
15.7.
Дана функция
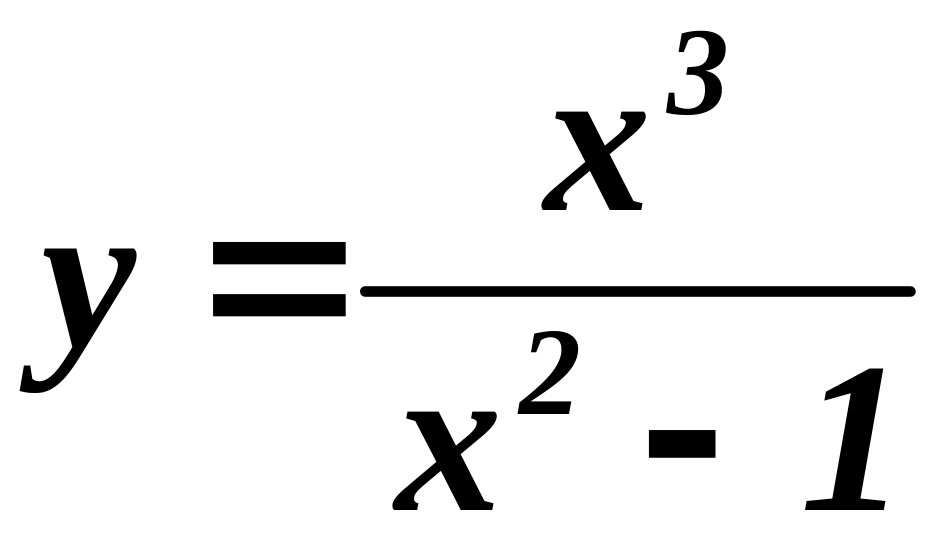 .
Найти асимптоты.
.
Найти асимптоты.
Вертикальные:
![]() - вертикальные асимптоты. Наклонные:
- вертикальные асимптоты. Наклонные:
![]()
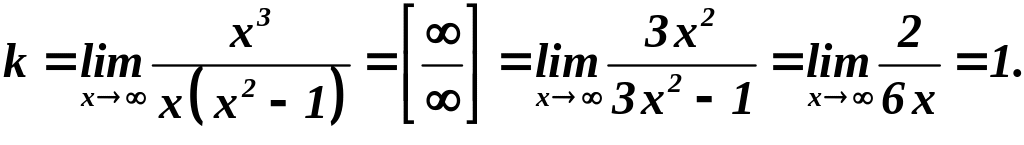
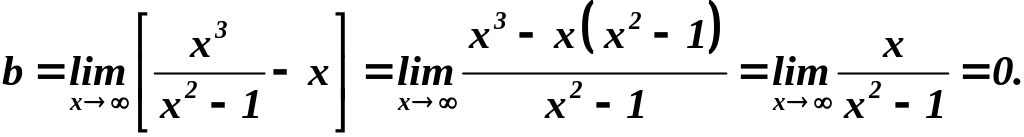
Следовательно,
наклонные асимптоты
![]() (биссектриса I
и III
координатных углов).
(биссектриса I
и III
координатных углов).
15.7. Общая схема исследования функции
Область определения функции.
Точки разрыва и интервалы непрерывности.
Асимптоты.
Точки пересечения графика с осями координат.
Четность нечетность графика (симметрия графика).
Интервалы монотонности. Экстремумы и значения функции в экстремумах.
Интервалы выпуклости, вогнутости функции, точки перегиба.
Пример
15.8.
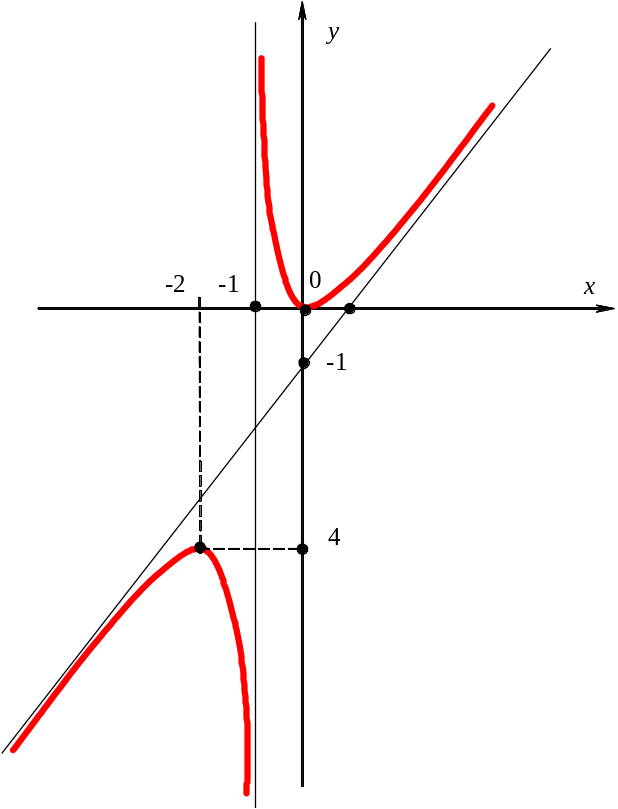
Исследовать функцию и построить её
график
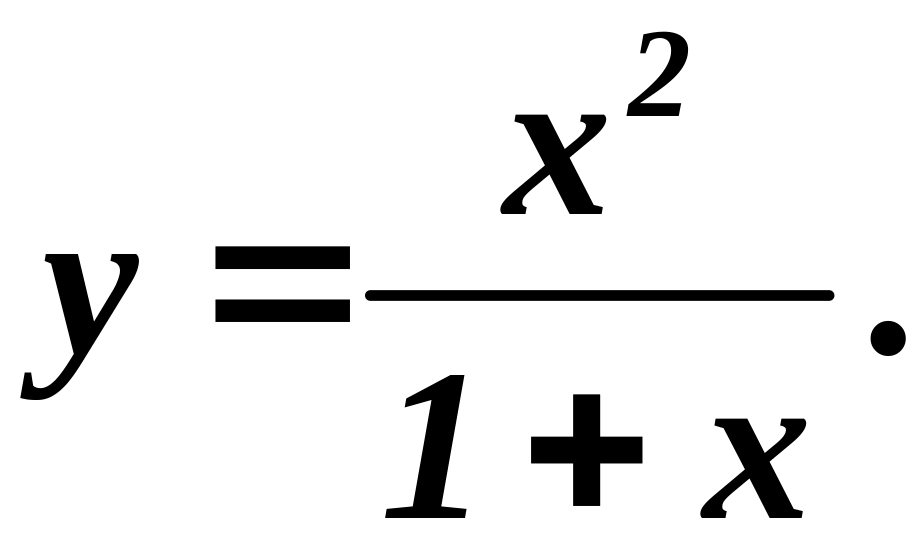
1.![]()
2.
![]() ,
точка разрыва
II рода,
т.к.
,
точка разрыва
II рода,
т.к.
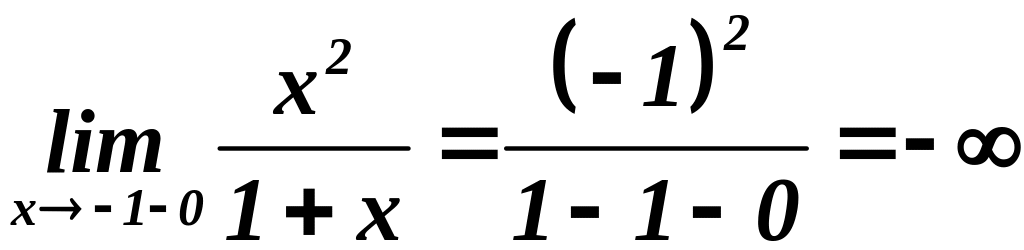
 -
интервалы непрерывности.
-
интервалы непрерывности.
3.
Наклонная
![]()
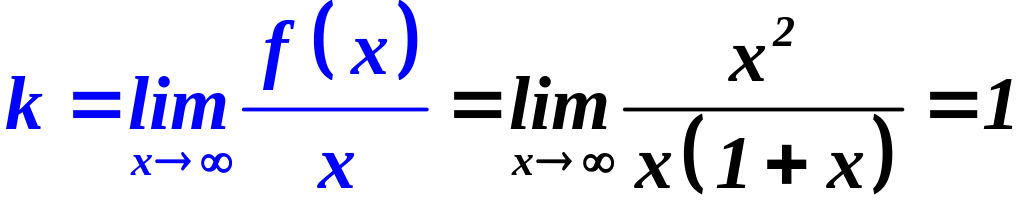
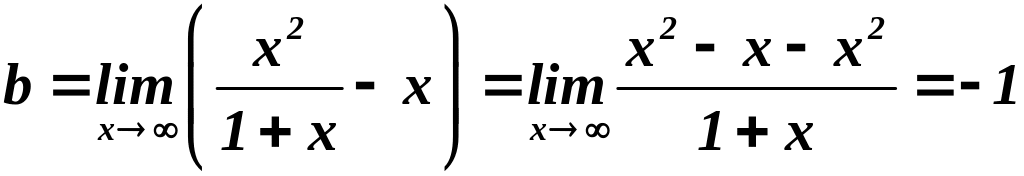 ;
;
![]() .
.
х |
0 |
1 |
у |
-1 |
0 |
4. Точки пересечения графика с осями:
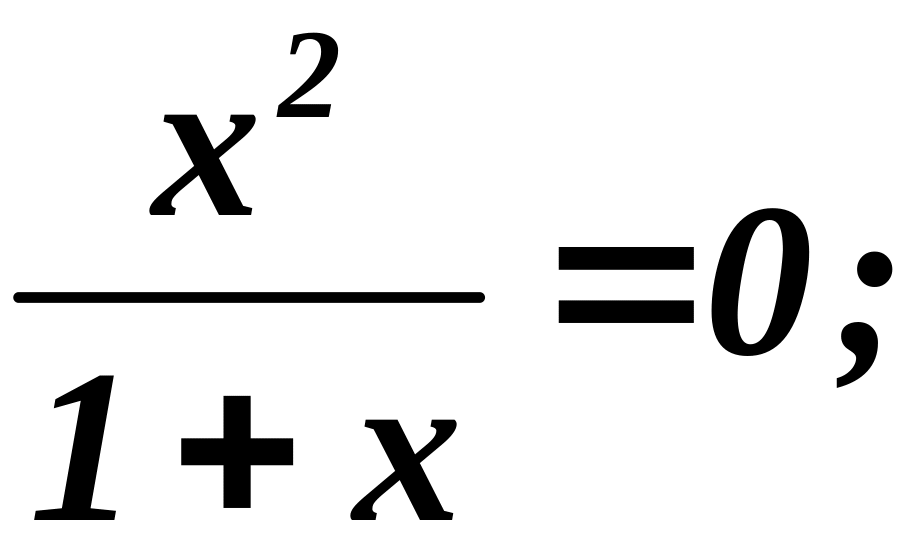
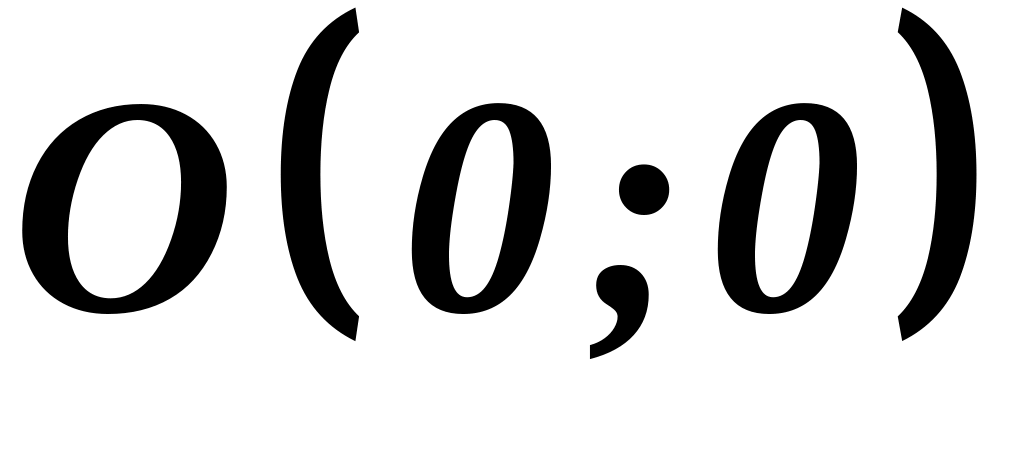
Если
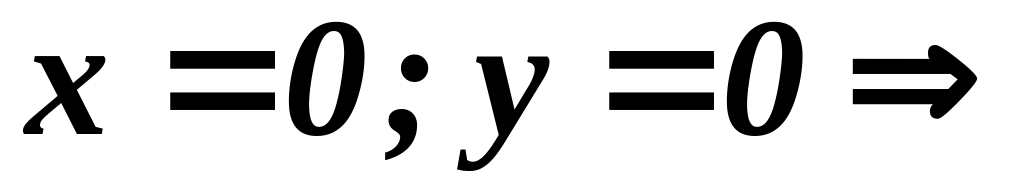 одна точка пересечения с осями координат.
одна точка пересечения с осями координат.
5. Четность, нечетность.
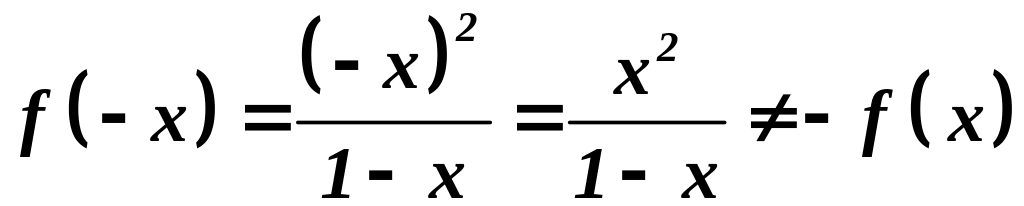 -
не является ни четной, ни нечетной,
следовательно, график несимметричен
ни относительно осей Ох
и Оу,
ни относительно начала координат
.
-
не является ни четной, ни нечетной,
следовательно, график несимметричен
ни относительно осей Ох
и Оу,
ни относительно начала координат
.
6.
Найдем производную:
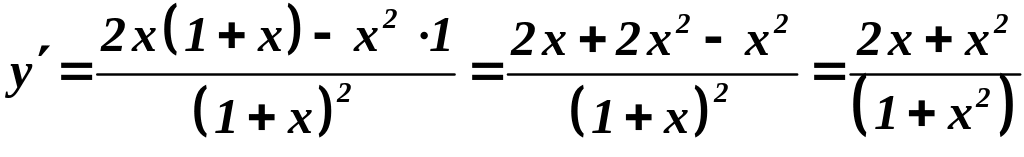 и приравняем ее к нулю:
и приравняем ее к нулю:
 .
критические точки;
производ-ная
.
критические точки;
производ-ная
![]() .
.
О
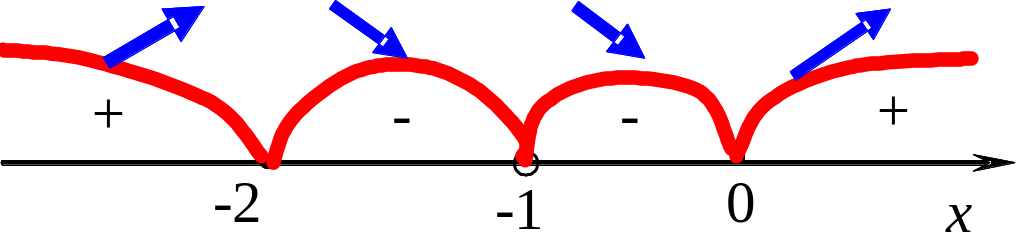
Точка
![]() - максимум;
- максимум;
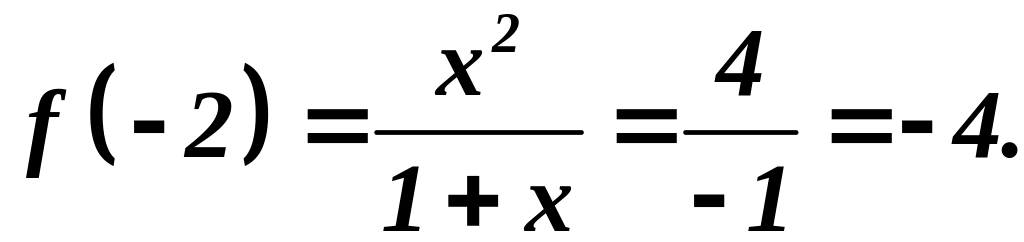 Точка
- минимум;
Точка
- минимум;
![]() .
.
7. Интервалы выпуклости, вогнутости функции, точки перегиба.
Найдем вторую производную:
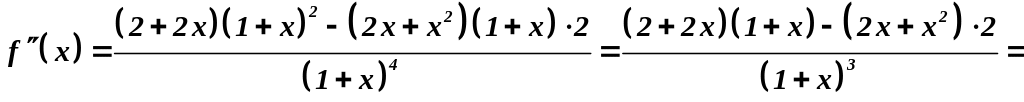
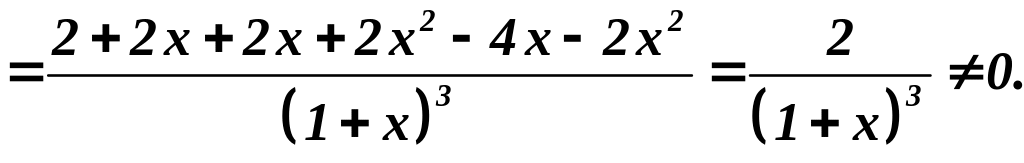
Точек перегиба нет.
Т
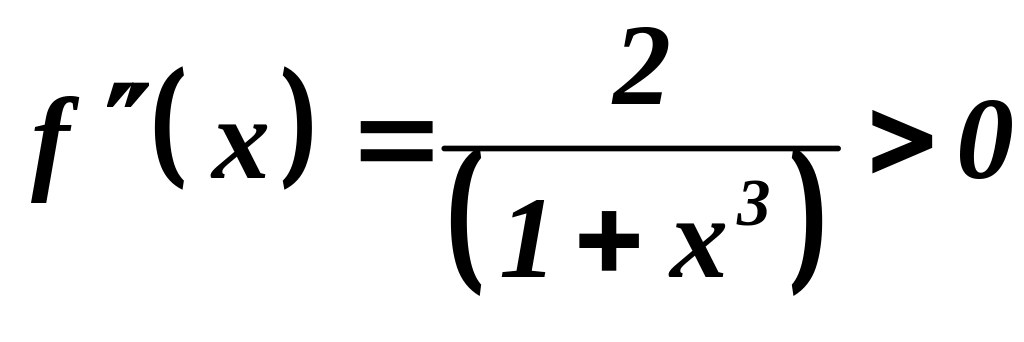 ,
то на промежутке
,
то на промежутке
![]() функция вогнута. Поскольку
функция вогнута. Поскольку
![]() ,
то на промежутке
,
то на промежутке
![]() функция выпуклая.
функция выпуклая.
Приложение производной и дифференциала алгоритмы действий.
1. Алгоритм нахождения критических точек функции.
1. Найти производную функции .
2. Найти точки, в которых или не существует.
2. Алгоритм исследования функции на монотонность.
Пусть дана дифференцируемая функция на интервале :
1. Находим ее производную .
2. Находим корни уравнения .
3. Разбиваем числовую прямую корнями на интервалы.
4. Определяем знак на каждом из интервалов.
5. Согласно признаку монотонности выносим заключение о монотонности.
3. Алгоритм исследования функции на экстремум (первое правило).
Пусть в интервале дана дифференцируемая функция .
1. Находим производную .
2.
Находим критические точки
,
то есть точки, в которых
или
![]() не существует.
не существует.
3.Определяем знак слева и справа от каждой из этих критических точек.
4.Согласно первому достаточному признаку существования экстремума выносим заключение об экстремуме.
5. Вычисляем значение функции в точках экстремума.
4. Алгоритм исследования функции на экстремум (второе правило).
1. Найти .
2.Найти стационарные точки, т.е. решить уравнение .
3. Найти .
4. Вычислить значения второй производной в стационарных точках.
5. Сделать вывод об экстремуме.
Заметим, что пользоваться вторым правилом обычно проще, чем первым, но второе правило имеет более узкий круг применения, а именно:
Если
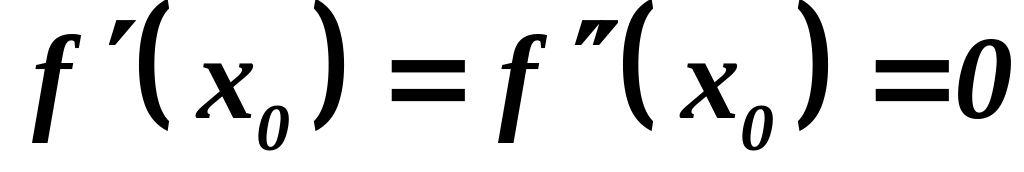 ,
то в точке
нельзя судить о наличии экстремума.
,
то в точке
нельзя судить о наличии экстремума.Если не существует, то
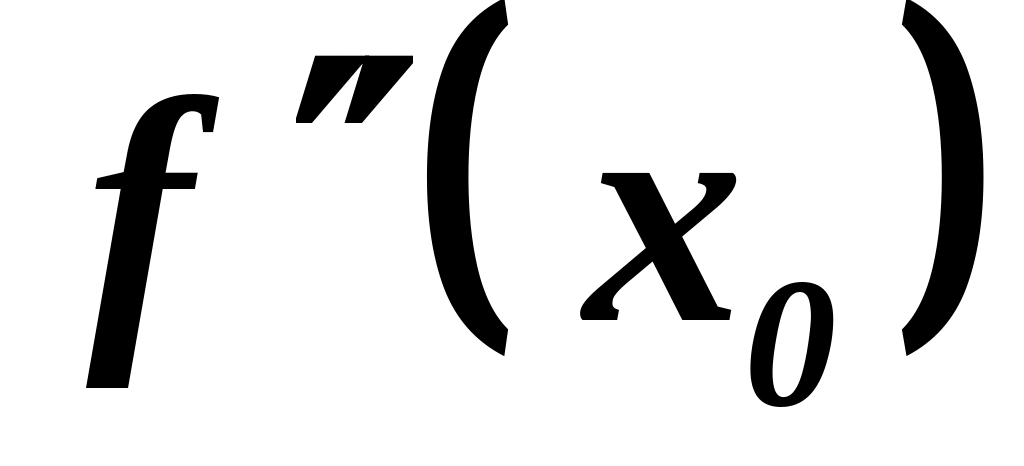 тоже не существует, т.е. второй достаточный
признак в этом случае тоже не применим,
и нужно воспользоваться первым
достаточным признаком.
тоже не существует, т.е. второй достаточный
признак в этом случае тоже не применим,
и нужно воспользоваться первым
достаточным признаком.
