Необходимый признак экстремума функции

Т

еорема 15.2.(признак Ферма). Функция может иметь экстремумы только в тех точках, в которых ее производная равна нулю или не существует.

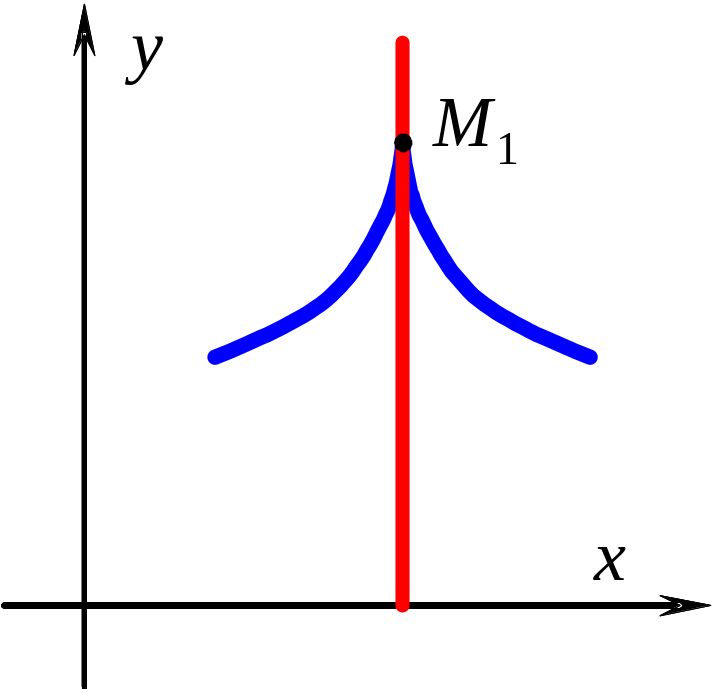
С геометрической точки зрения тот факт, что , по теореме Ролля означает, что касательная в точке х параллельна оси Ох, а тот факт, что - не существует, означает, что - не дифференцируема (см. рисунки). Примеры таких функций:

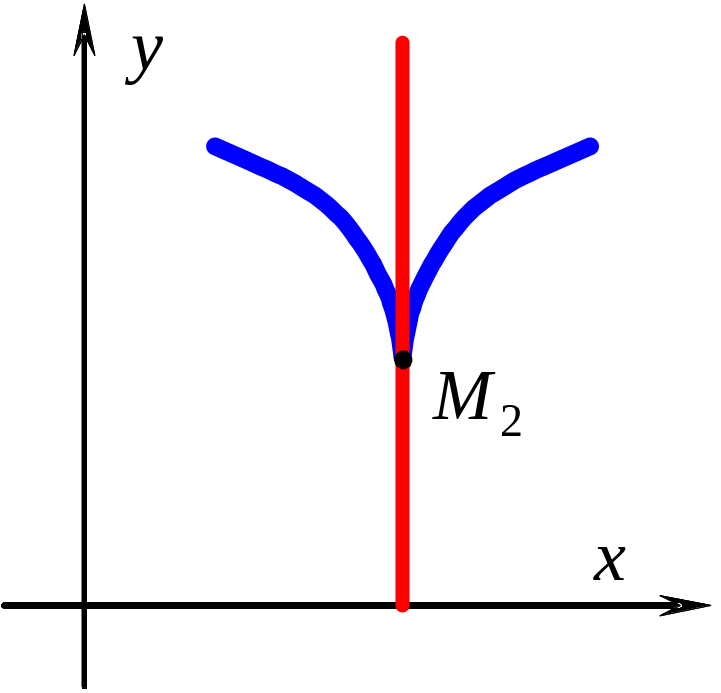
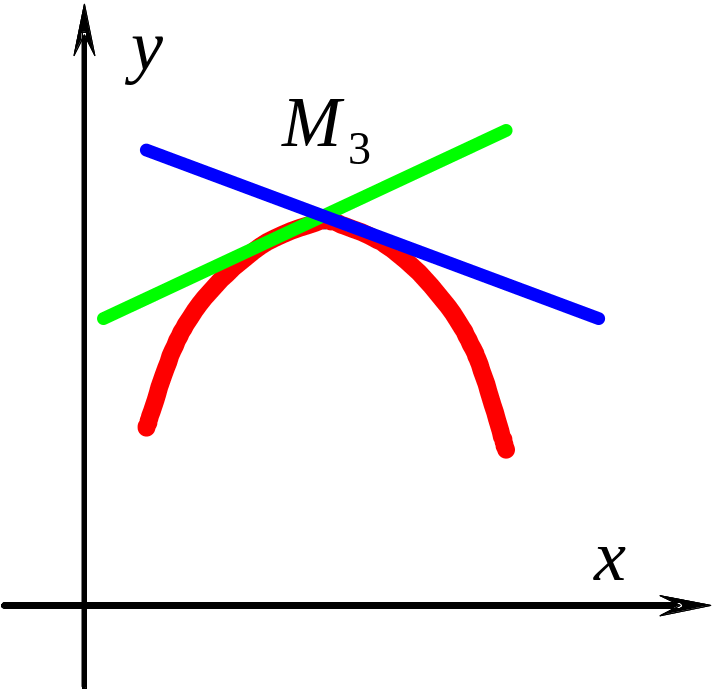
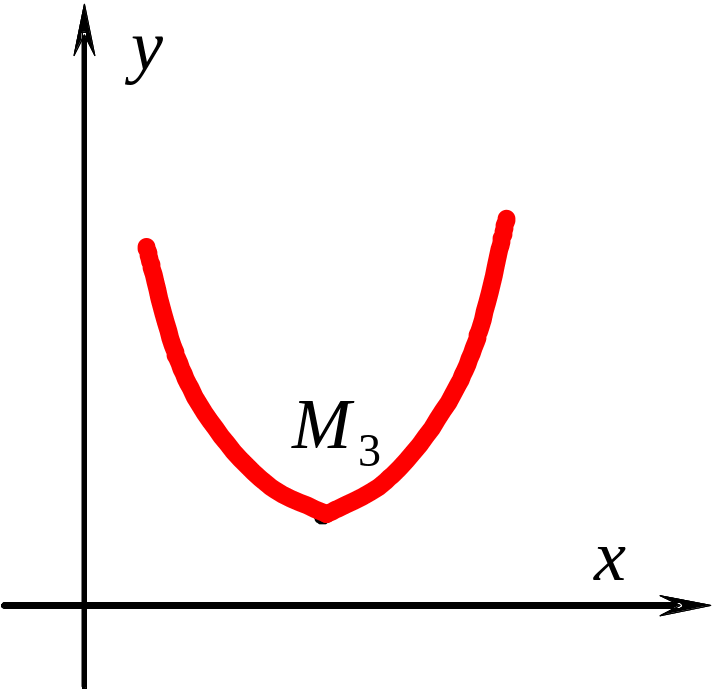
В точках и касательная параллельна оси Оу. Такие точки называются точками возврата.

В точках и касательная переходит внезапно от одного положения к другому, то есть, в этой точке нет, определенной касательной – угловые точки. Необходимый признак не является достаточным.

Пример 15.2. , но производная не меняет знака, на всей числовой оси, следовательно, точка - не экстремум. Когда же точка будет экстремумом? Ответ на этот вопрос даёт следующая теорема.

Первый достаточный признак экстремума

Теорема 15.3. Точка является точкой экстремума функции , если производная при переходе через точку меняет знак, причем: с «+» на «-»  max , с «-» на «+»  min.

15.3. Схема исследования функции на экстремумы,

промежутки монотонности. Наибольшее и наименьшее

значения функции на интервале

Пусть дана функция .

1. Находим производную ;

2. Находим стационарные точки ;

3. Находим точки, в которых производная функции не существует (если это дробь, то знаменатель не равен 0). Обозначим все найденные точки в порядке возрастания . Это те точки, в которых функция может иметь экстремумы. Их называют критическими (это стационарные точки и те точки, в которых производная не существует). Наносим все эти точки на числовую ось.

4. На каждом промежутке находим знак производной, а затем определяем ее монотонность. Выясняем, в каких точках производная меняет знак, следовательно, это максимум или минимум.

5. Подстановкой в выражение функции критических значений, находим наибольшее и наименьшее значение функции.

В нашем примере:

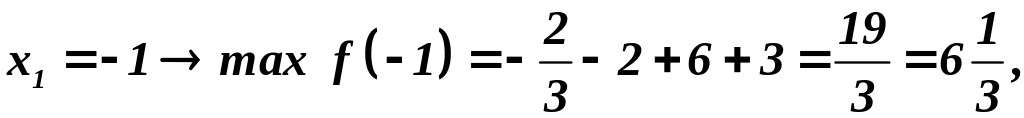
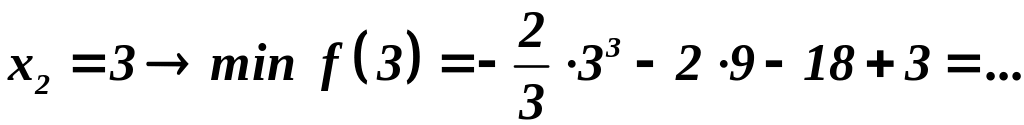
После того, как экстремумы найдены, то можно легко найти наибольшее и наименьшее значение функции на интервале . Для этого нужно сравнить между собой значения функции в экстремумах и на концах интервала. В

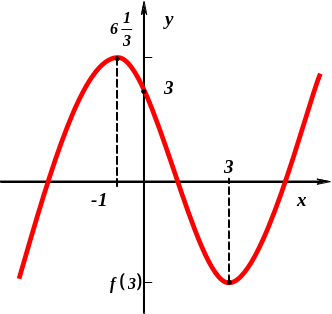
нашем примере на интервале точки экстремума совпадают с концами интервала, следовательно

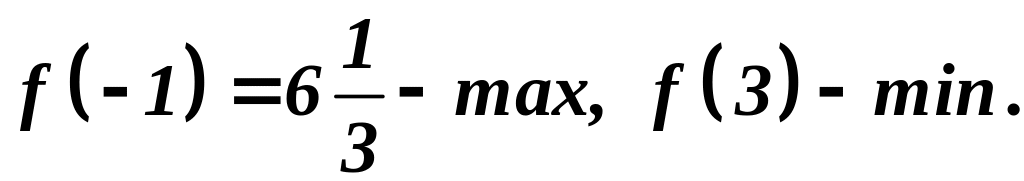
15.4. Применение второй производной к исследованию функции Второй достаточный признак экстремума.

Точка есть точка экстремума функции , если, , а , причем если , то - точка минимума, если , то точка максимума.

В том случае, когда вторая производная , пользоваться этим признаком нельзя и нужно обратиться к 1 достаточному признаку.

П

ример 15.3.

, ,

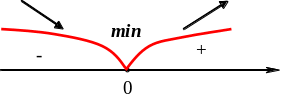
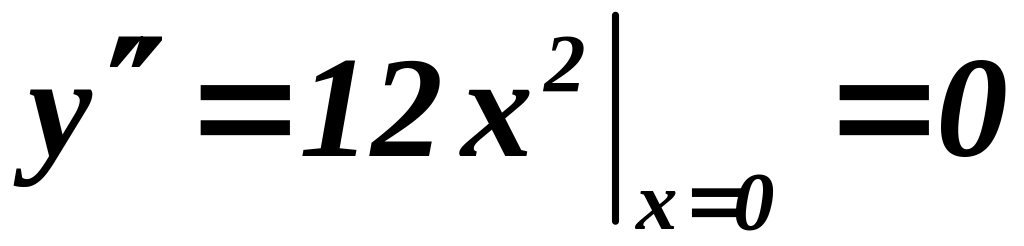, а по I признаку - минимум.

15.5. Выпуклость и вогнутость линии. Точки перегиба

Определение 15.3. Дуга называется выпуклой, если она пересекается с любой своей секущей, не более чем в двух точках.

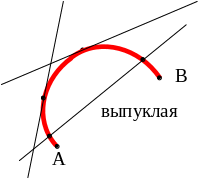
Если дуга выпуклая, то она лежит по одну сторону касательной в любой ее точке.

Будем рассматривать дуги, которые являются частями графика линий непрерывных функций. Линии, обращенные выпуклостью вверх, называются выпуклыми, а вниз – вогнутыми.

Определение 15.4. Точка на линии называется точкой перегиба, если она разделяет выпуклую дугу от вогнутой.

Пример 15.4. Рассмотрим : 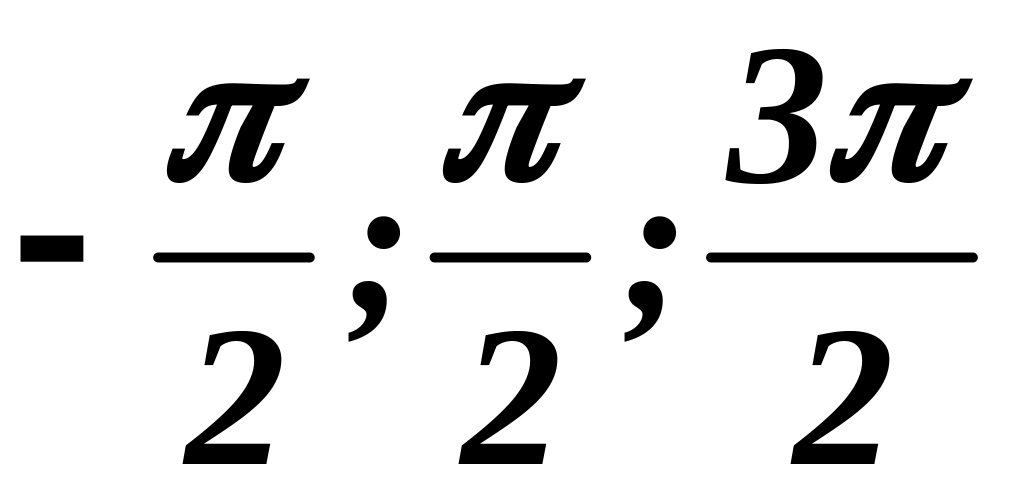- точки перегиба.

К

асательная в точке перегиба пересекает линию и параллельна Оу. Связь между второй производной и выпуклостью (вогнутостью) устанавливается следующими теоремами.

Теорема 15.4. (необходимый признак): Если дуга линии выпуклая, то (неположительная). Если дуга линии вогнутая, то (неотрицательная) в соответствующем интервале.

Теорема 15.5. (достаточный признак): Если всюду на некотором интервале, то дуга линии выпуклая. Если , то дуга – вогнутая.

Если - абсцисса точки перегиба, то , и меняет знак при переходе через . При перемене знака с «-» на «+» слева лежит выпуклый участок, а справа – вогнутый, с «+» на «-» - наоборот.