Геометрический смысл теоремы Лагранжа

Геометрический смысл изображен следующим графиком. Обозначим через - угол наклона к секущей .

Из но

П

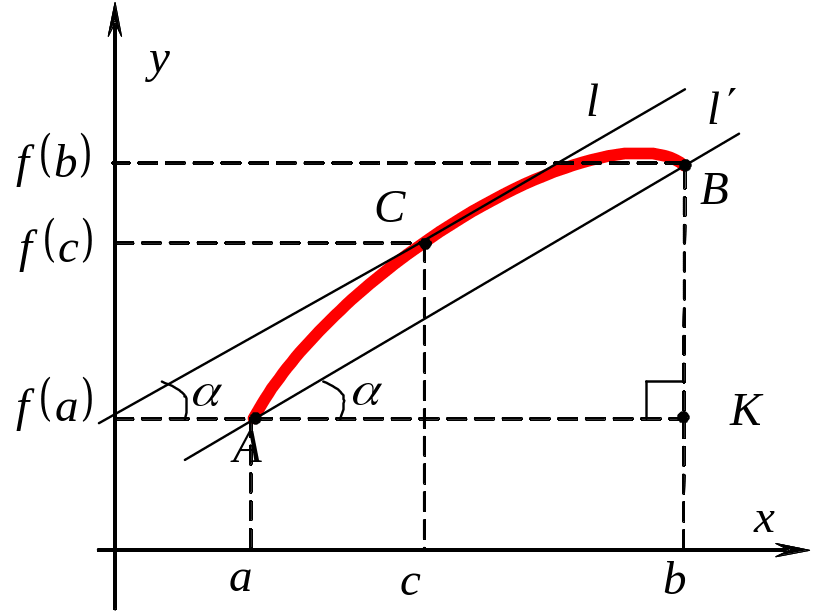
о формуле Лагранжа - есть угловой коэффициент хорды .

Так как угловой коэффициент касательной равен угловому коэффициенту хорды, то касательная и хорда параллельны. Геометрический смысл теоремы состоит в том, что на дуге найдется такая точка , с общей абсциссой с, касательная в которой параллельна хорде.

Заметим, что теорема Ролля является частным случаем теоремы Лагранжа, когда

14.8.4. Теорема Коши (1789-1857)

Теорема 14.4. Если и непрерывны на отрезке , дифференцируемы, на интервале , причем , то между точками и найдется такая точка , что имеет место равенство:

.

14.8.5. Правило Лопиталя (1661-1704)

Правило Лопиталя применяется для раскрытия неопределенностей вида

Теорема 14.5. Пусть и - определены в некоторой окрестности точки , за исключением, быть может, самой точки и удовлетворяет условиям:

1. т.е. и - бесконечно малые;

2. и - дифференцируемые функции;

3. 

Тогда этот предел равен: .

Аналогично, для случаев .

Пример 14.15.

1)

2)

Заметим, что все другие неопределенности - сводятся к тоже могут быть раскрыты по правилу Лопиталя.

Полезны следующие преобразования:

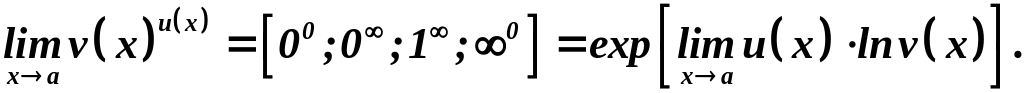
Лекция 15. Применение дифференциального исчисления к исследованию функции

15.1. Признаки монотонности функции

Одно из самых важных назначений дифференциального исчисления – это применение его к исследованию функций (линий). Эта процедура опирается на весьма простую связь между поведением функции и свойствами ее производных.

Теорема 15.1. (Необходимый и достаточный признак монотонности).

1. Если функция в интервале возрастает, то её производная - неотрицательная.

2. Если - убывает, то её производная неположительная .

3. Если , (то есть не изменяется), то

Г

еометрический смысл теоремы

Если подвижная точка при движении по графику функции слева на право поднимается, то касательная к графику функции образует острый угол с осью Ох ; если же точка опускается, то касательная образует тупой угол, .

В интервале монотонности функции знак её производной не может изменяться на противоположный.

Достаточный признак монотонности читается из теоремы в обратном порядке.

Пример 15.1. Исследовать на монотонность функцию:

Решение: Найдем: Приравняем , то есть

.

Вся числовая ось разбивается на три интервала:

1. функция возрастает;

2. функция убывает;

3. функция возрастает.

Определение 15.1. Те, значения , в которых производная обращается в нуль, называются стационарными точками функции.

Как видно из нашего примера - в этих точках функция меняет характер своего поведения, сначала возрастает, потом убывает и т.д.

15.2. Экстремумы функции

Определение 15.2. Точка называется точкой максимума функции , если , есть наибольшее значение функции в окрестности точки . Точка - минимум, если - наименьшее значение функции в окрестности точки . Точки максимум и минимум объединяются названием точки экстремума.