
- •14.8. Основные теоремы дифференциального исчисления
- •14.8. 1. Теорема Ферма (1601-1665гг)
- •Предположим, что т.Е. То будем иметь:
- •Геометрический смысл теоремы Ферма
- •14.8.2. Теорема м. Ролля (1652-1719)
- •Геометрический смысл теоремы Ролля
- •14.8.3. Теорема Лагранжа (1736-1813)
- •Геометрический смысл теоремы Лагранжа
- •14.8.4. Теорема Коши (1789-1857)
- •14.8.5. Правило Лопиталя (1661-1704)
- •Лекция 15. Применение дифференциального исчисления к исследованию функции
- •15.1. Признаки монотонности функции
- •15.2. Экстремумы функции
- •Необходимый признак экстремума функции
- •15.4. Применение второй производной к исследованию функции Второй достаточный признак экстремума.
- •15.5. Выпуклость и вогнутость линии. Точки перегиба
- •15.6. Асимптоты линий
- •15.7. Общая схема исследования функции
- •5. Алгоритм исследования функции на выпуклость и точки перегиба.
- •6. Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке .
- •7. Алгоритм отыскания асимптоты графика функции .
- •8. Алгоритм исследования и построения графика функции.
14.8. Основные теоремы дифференциального исчисления
14.8. 1. Теорема Ферма (1601-1665гг)
Теорема 14.1.
Пусть функция
![]() определена на отрезке
определена на отрезке
![]() и во внутренней точке с
этого отрезка принимает наибольшее и
наименьшее значение. Тогда, если
и во внутренней точке с
этого отрезка принимает наибольшее и
наименьшее значение. Тогда, если
![]() существует производная
существует производная
![]() ,
то она равна 0,
т.е.
,
то она равна 0,
т.е.
![]() .
.
![]()
Доказательство:
Докажем
для случая, когда функция принимает в
точке с
наибольшее значение, т.е.
![]()
Пусть
![]() определена на отрезке
определена на отрезке
![]() и во внутренней точке с
этого отрезка принимает наибольшее
значение:
В точке с
существует производная
и во внутренней точке с
этого отрезка принимает наибольшее
значение:
В точке с
существует производная
![]() Требуется доказать, что
Требуется доказать, что
![]()
Дадим
точке с
приращение
![]() так как
так как
![]() не вышла за пределы
запишем
не вышла за пределы
запишем
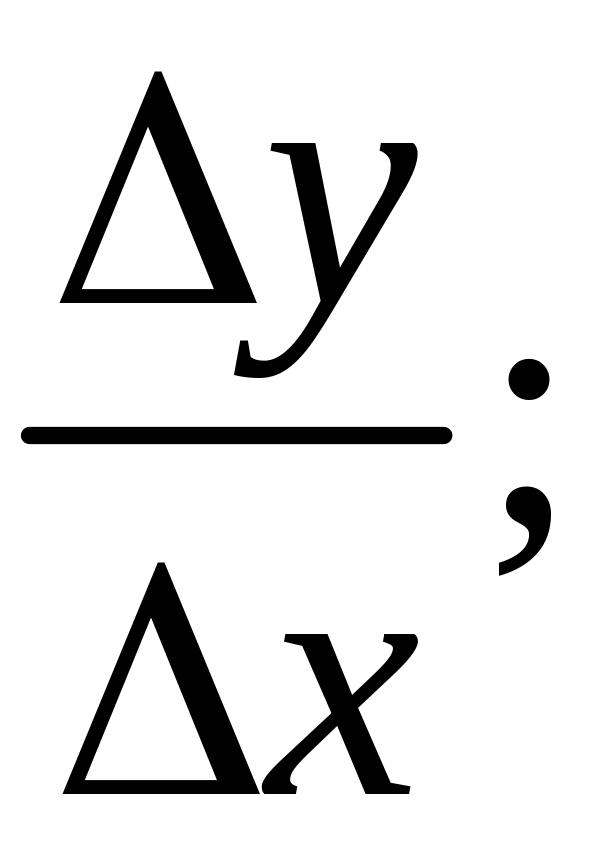
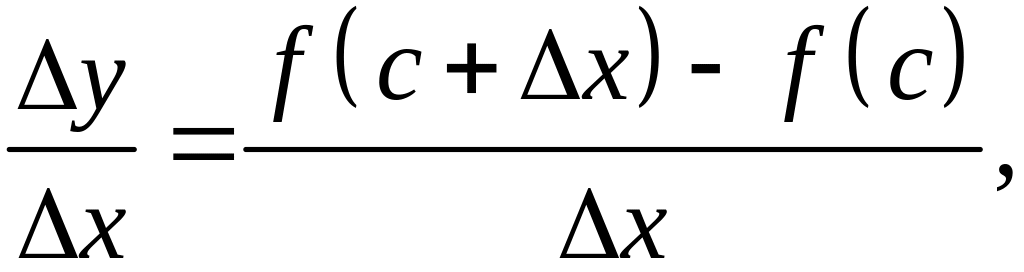 в точке с,
функция принимает наибольшее значение,
то
в точке с,
функция принимает наибольшее значение,
то
![]()
![]()
Предположим, что
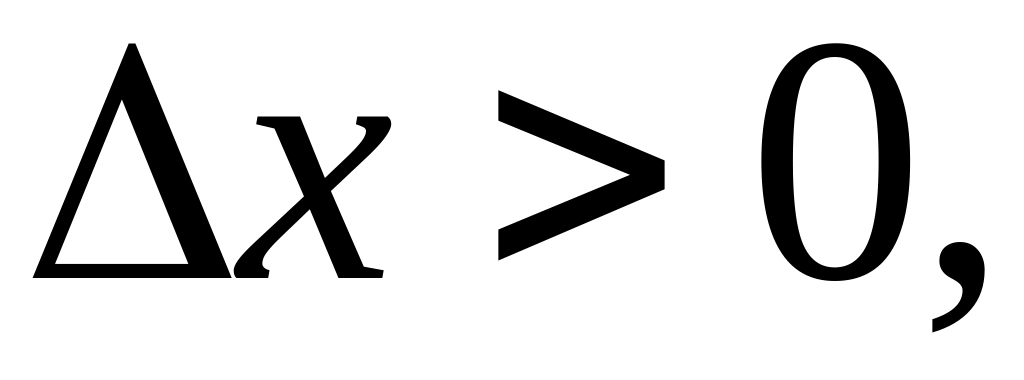 т.е.
т.е.
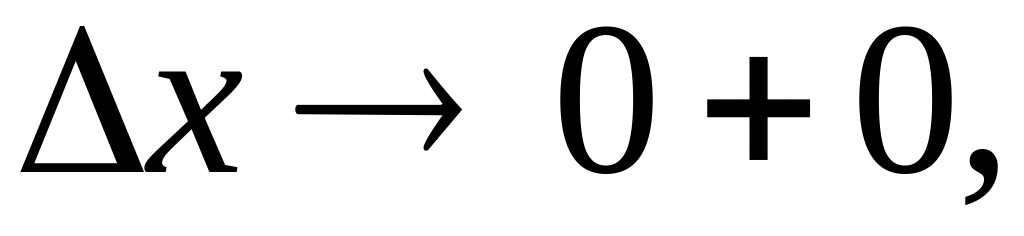 то будем иметь:
то будем иметь:

Переходя
к пределу:
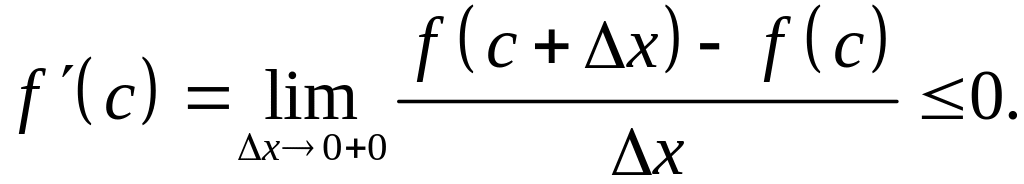
Предположим, что т.Е. То будем иметь:
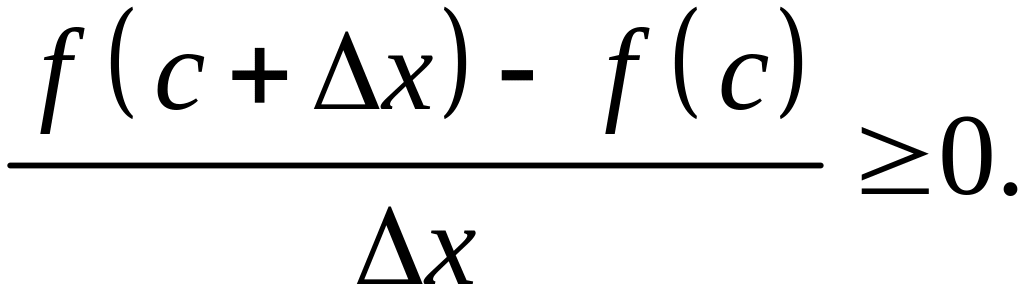 Переходя к пределу:
Переходя к пределу:
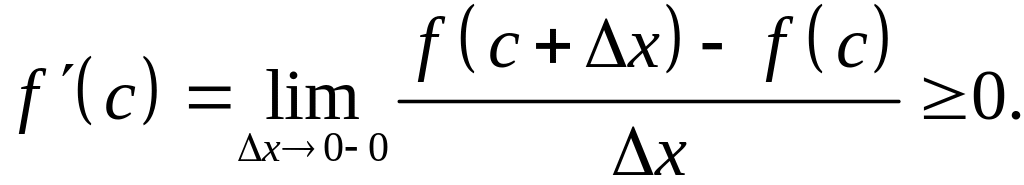
Из
двух неравенств
![]() следует, что
.
следует, что
.
Аналогично,
когда в точке
![]() ,
функция достигает своего наименьшего
значения. Т
,
функция достигает своего наименьшего
значения. Т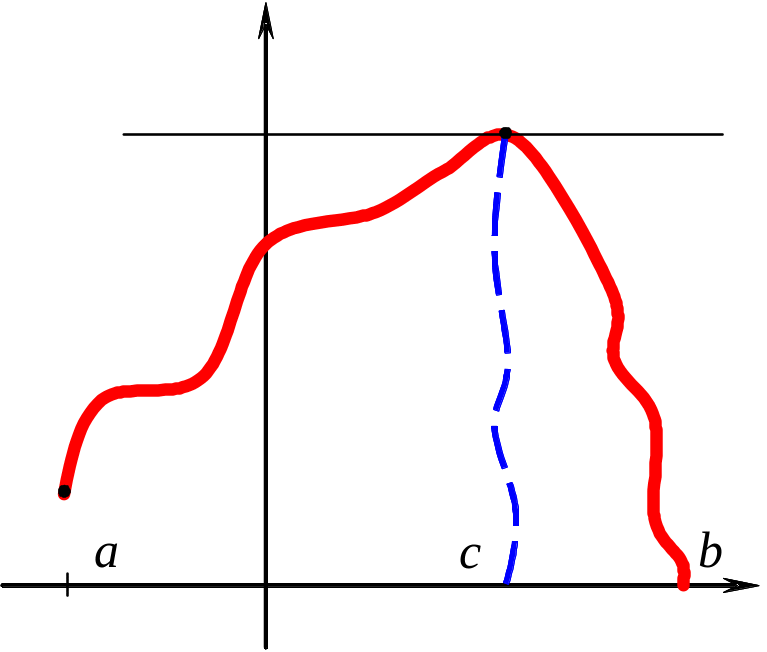
Геометрический смысл теоремы Ферма
Вспомним
геометрический смысл производной в
точке
:
![]() - угловой коэффициент касательной в
точке
,
а если
,
то касательная
параллельна оси Ох.
- угловой коэффициент касательной в
точке
,
а если
,
то касательная
параллельна оси Ох.
14.8.2. Теорема м. Ролля (1652-1719)
Теорема 14.2.
Если функция
непрерывна на отрезке
,
дифференцируема на интервале
![]() и на концах интервала
принимает равные значения
и на концах интервала
принимает равные значения
![]() ,
то между точками
,
то между точками
![]() найдется, по крайней мере, одна точка
:
.
найдется, по крайней мере, одна точка
:
.
Д
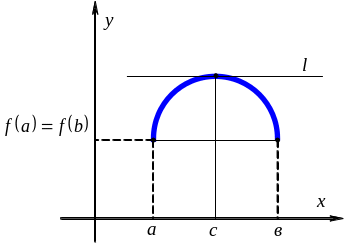
Пусть для функции условия теоремы выполняются. Т.к. непрерывна на отрезке по теореме 2 Вейерштрасса она принимает на этом отрезке свои наибольшие и наименьшие значения: М и т.
Рассмотрим два случая:
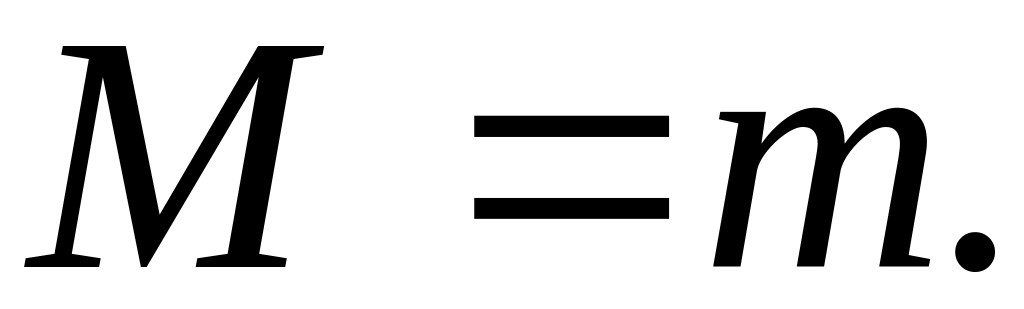 По
определению наибольшего и наименьшего
значения
По
определению наибольшего и наименьшего
значения
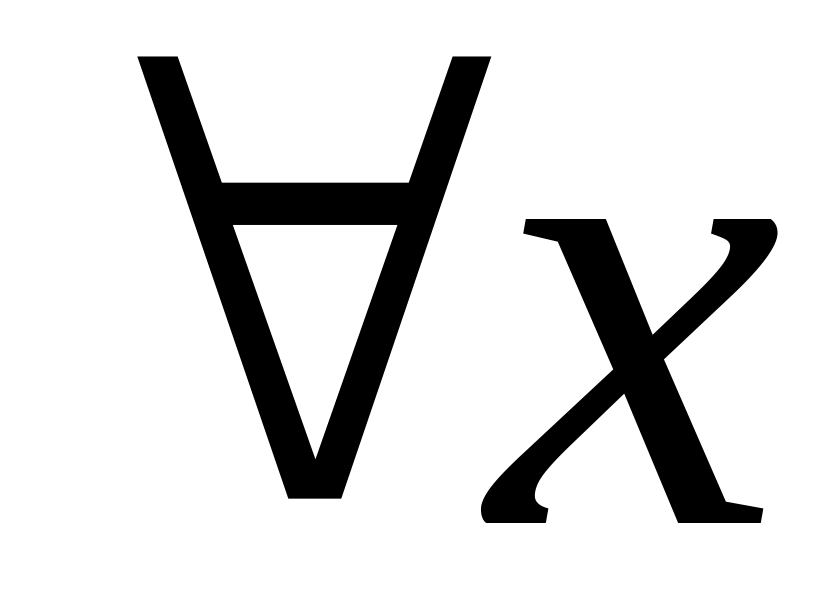 из отрезка
выполняется неравенство:
из отрезка
выполняется неравенство:
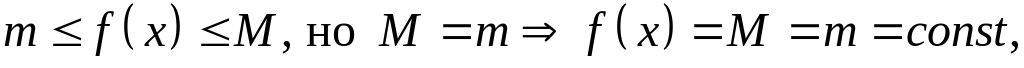 а производная от
а производная от
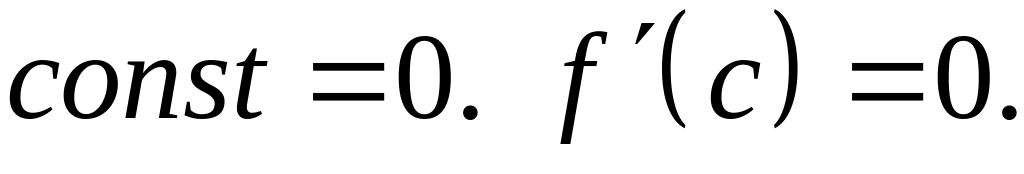
 Оба
эти значения функция достигает на
отрезке
и так как по условию теоремы
Оба
эти значения функция достигает на
отрезке
и так как по условию теоремы
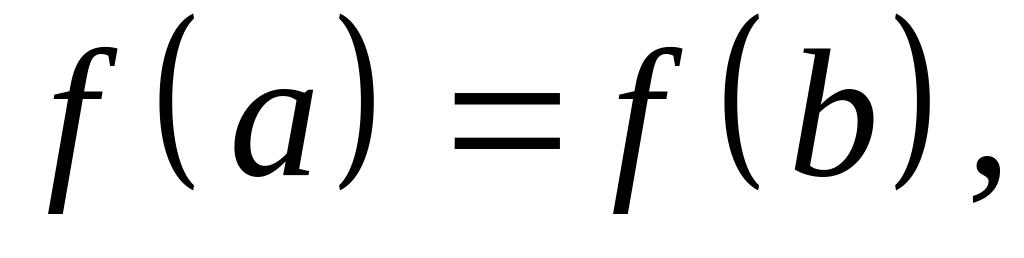 то оба эти значения
то оба эти значения
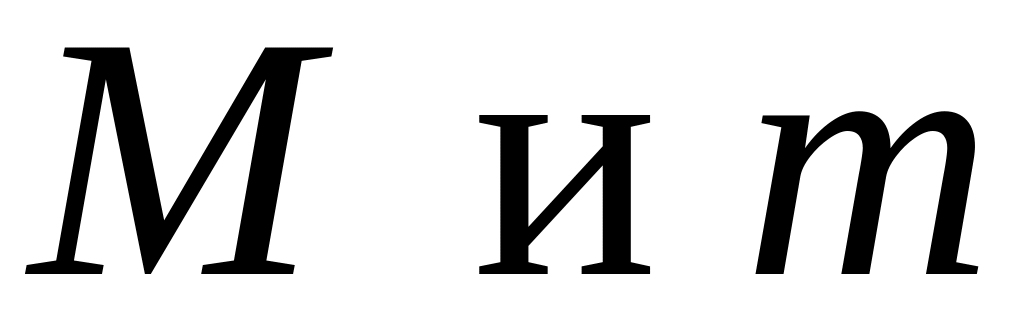 не могут достигаться одновременно на
концах
.
Значит, одно из этих значений достигается
внутри интервала
не могут достигаться одновременно на
концах
.
Значит, одно из этих значений достигается
внутри интервала
 ,
то есть в точке
,
то есть в точке
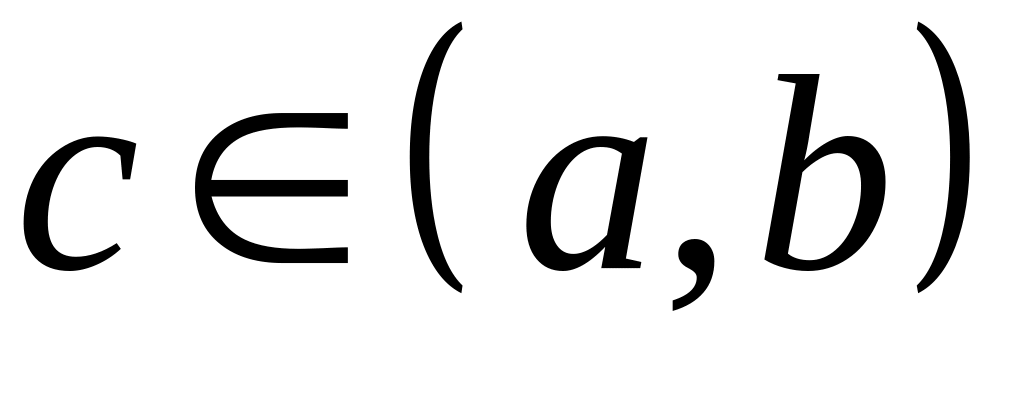 .
В таком случае, мы находимся в условии
теоремы Ферма, на основании которой
Теорема доказана.
.
В таком случае, мы находимся в условии
теоремы Ферма, на основании которой
Теорема доказана.
Геометрический смысл теоремы Ролля
Если
,
то
- есть угловой коэффициент касательной
и
,
следовательно, касательная параллельна
![]() .
Смысл в том, что найдется такая точка
.
Смысл в том, что найдется такая точка
![]() ,
в которой касательная к ней параллельна
оси
.
,
в которой касательная к ней параллельна
оси
.
14.8.3. Теорема Лагранжа (1736-1813)
Теорема
14.3.
Если
функция непрерывна на отрезке
и дифференцируемая на промежутке
,
то между точками
![]() и
и
![]() найдется, такая точка
,
что имеет место равенство:
найдется, такая точка
,
что имеет место равенство:
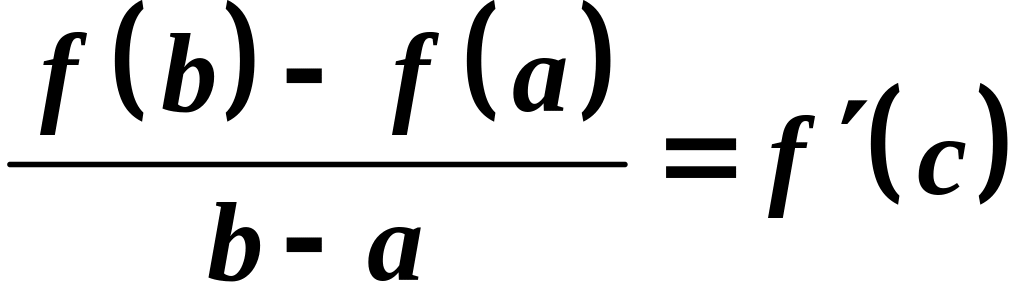 .
.
Доказательство:
Пусть
- непрерывна на отрезке
и дифференцируема на промежутке
![]() Рассмотрим вспомогательную функцию
Рассмотрим вспомогательную функцию
 ,
где
,
где
![]() -
удовлетворяет условию теоремы Ролля
на отрезке
.
В самом деле, она непрерывна на отрезке
,
как алгебраическая сумма непрерывных
функций, следовательно, она дифференцируема
на промежутке
Ее производная равна:
-
удовлетворяет условию теоремы Ролля
на отрезке
.
В самом деле, она непрерывна на отрезке
,
как алгебраическая сумма непрерывных
функций, следовательно, она дифференцируема
на промежутке
Ее производная равна:
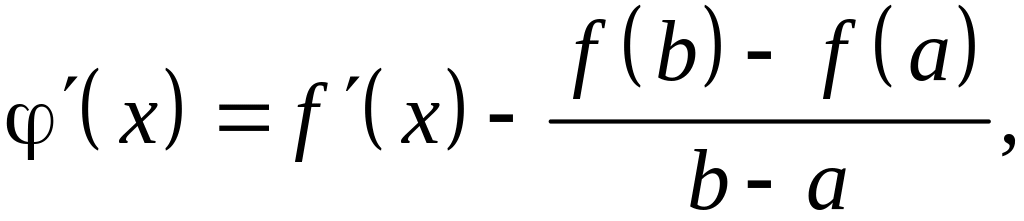
![]() достигается
непосредственным вычислением. На
основании теоремы Ролля между точками
достигается
непосредственным вычислением. На
основании теоремы Ролля между точками
![]() существует такая точка с,
что
существует такая точка с,
что
![]()
Но
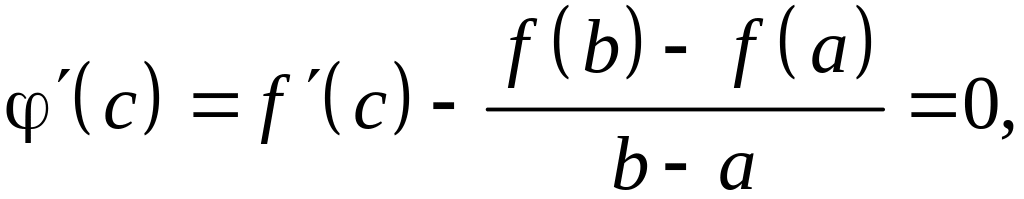
Отсюда,
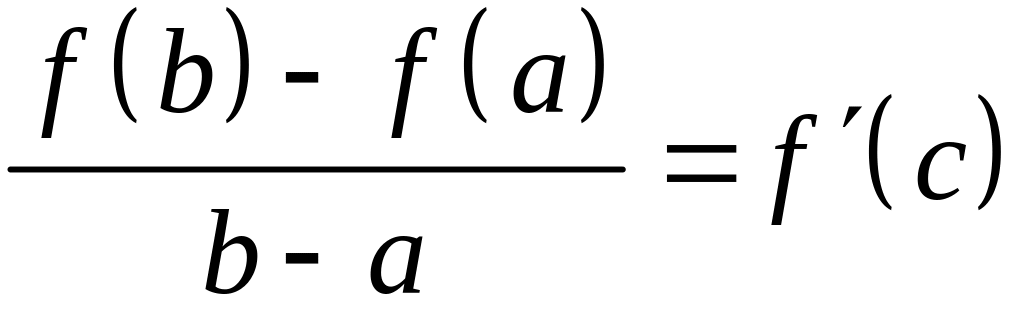 .
Теорема доказана.
.
Теорема доказана.
Доказанная в теореме формула носит название формулы Лагранжа.
