- •Модуляция
- •Мощность амплитудно-модулируемого сигнала
- •Спектр частотно-модулированных сигналов
- •Свободные колебания в контуре
- •Определение мощности
- •Линейный четырехполюсник
- •Параллельный контур
- •Влияние сопротивлений генератора и нагрузки на свойства последовательного контура
- •Прохождение модулированных колебаний через контур- фильтр
- •Связанные контуры
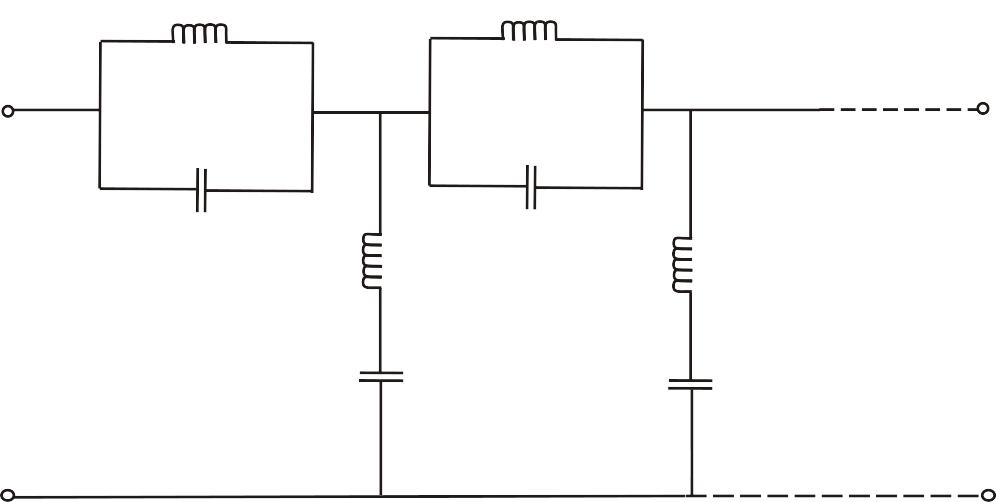
- •Линейные цепи с распределенными параметрами
- •Характеристика длинных линий
- •Отражение волн в линии
- •Антенны
- •Основные параметры антенны
- •Характеристики антенны на излучение и прием абсолютно одинаковы
- •Применение р-n перехода.
- •Выходные характеритики транзистора с общей базой
- •Условные обозначения полевых транзисторов Сравнение полевых и биполярных транзисторов
- •Интегральные микросхемы.
- •Характеристики усилителей.
- •Причины искажений
- •Частотные характеристики усилителя.
- •Классификация усилителей.
- •Резисторный усилитель звуковой частоты на транзисторе.
- •Частные характеристики усилителя.
- •Недостатки схемы:
Параллельный контур
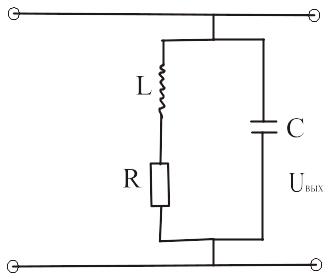 Здесь
Ri
– омическое сопротивление витков
катушки.
Здесь
Ri
– омическое сопротивление витков
катушки.
Комплексное сопротивление цепи:  причем ωL
причем ωL![]() R.
R.
В числителе " R" - мы можем пренебречь, а в знаменателе R нельзя пренебречь, так как знаменатель может превратиться в 0 при ω=ω0.
![]()
![]() квадрат
характеристического сопротивления.
квадрат
характеристического сопротивления.
![]() ;
;![]() -
полное сопротивление (
-
полное сопротивление (![]() ;
ρ=
;
ρ=![]() )
)

![]() ;
;
![]()


![]()
Влияние сопротивления генератора и нагрузки на свойства параллельного контура
 Rг-
сопротивление генератора
Rг-
сопротивление генератора
![]() (
(![]() -
сопротивления контура,
-
сопротивления контура, ![]() – общее сопротивление)
– общее сопротивление)
Амплитуда:![]() ; (=
; (= ![]() -
контур на ток не влияет)
-
контур на ток не влияет)
![]()
Коэффициент передачи: ![]()
Рассмотрим 2 случая
 -
очень мало, т.к.
-
очень мало, т.к. 
![]() .
Тогда резонансные свойства контура
практически не проявляются
.
Тогда резонансные свойства контура
практически не проявляются

 ;
;


Влияние сопротивления нагрузки

 ,
если
,
если  ,
то
,
то 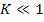 т. к.
т. к.  очень мало.
очень мало. - нагрузка не влияет на свойства контура.
И сопротивление генератора и сопротивление
нагрузки должно быть большим, в этом
случае проявляются резонансные свойства
контура.
- нагрузка не влияет на свойства контура.
И сопротивление генератора и сопротивление
нагрузки должно быть большим, в этом
случае проявляются резонансные свойства
контура.
Влияние сопротивлений генератора и нагрузки на свойства последовательного контура

![]() -
собственная частота
-
собственная частота
=![]() – не меняется
– не меняется
ρ = ![]() (характеристическое сопротивление) не
изменяется
(характеристическое сопротивление) не
изменяется
Q=![]() →добротность
уменьшается
→добротность
уменьшается
 Как
влияет 𝑅
нагрузки:
Как
влияет 𝑅
нагрузки:
 ,
,
 -
сопротивление конденсатора 𝐾
-
сопротивление конденсатора 𝐾 1,
1, -
мало
-
мало нагрузка не влияет на свойства контура
нагрузка не влияет на свойства контура
![]() -входное сопротивление)
-входное сопротивление)
![]() -
должно быть как можно больше,
-
должно быть как можно больше, ![]() -
как можно меньше.
-
как можно меньше.
Прохождение модулированных колебаний через контур- фильтр
Чтобы получить спектр выходного сигнала необходимо умножить спектр входного сигнала на амплитудно- частотную характеристику (𝑈=𝑈(ω))
 ,
умножаем графически
,
умножаем графически

 Собственная частота сигнала = несущей
частоте контура. (т.е. контур сделали
качественным)
Собственная частота сигнала = несущей
частоте контура. (т.е. контур сделали
качественным)



![]()
m - коэффициент модуляции, уменьшается
Сигнал искажается
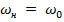 (собственная частота контура = несущей
частоте сигнала)
(собственная частота контура = несущей
частоте сигнала)
![]()
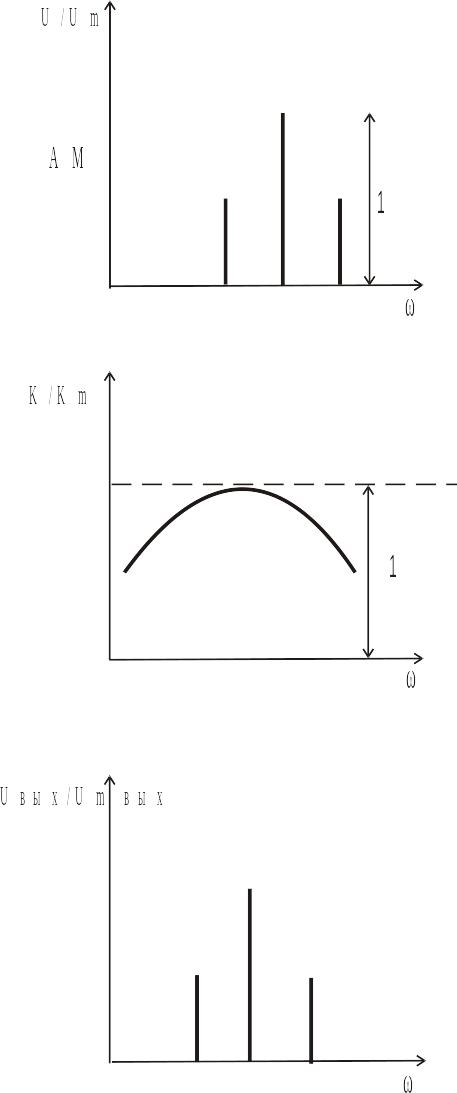
Искажения информации минимальны
Для согласования фильтра и сигнала необходимо, чтобы:
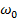 (собственная частота) фильтра совпадала
с несущей частотой сигнала;
(собственная частота) фильтра совпадала
с несущей частотой сигнала;Ширина полосы фильтра была бы не меньше ширины полосы сигнала.
Связанные контуры
Идеальный фильтр должен иметь П-образную частотную характеристику и линейную фазовою характеристику в полосе пропускания. Для приближения частотной характеристики к идеальной используется система нескольких контуров, связанных между собой либо общим магнитным полем (индуктивная связь), либо общим электрическим полем (емкостная связь).
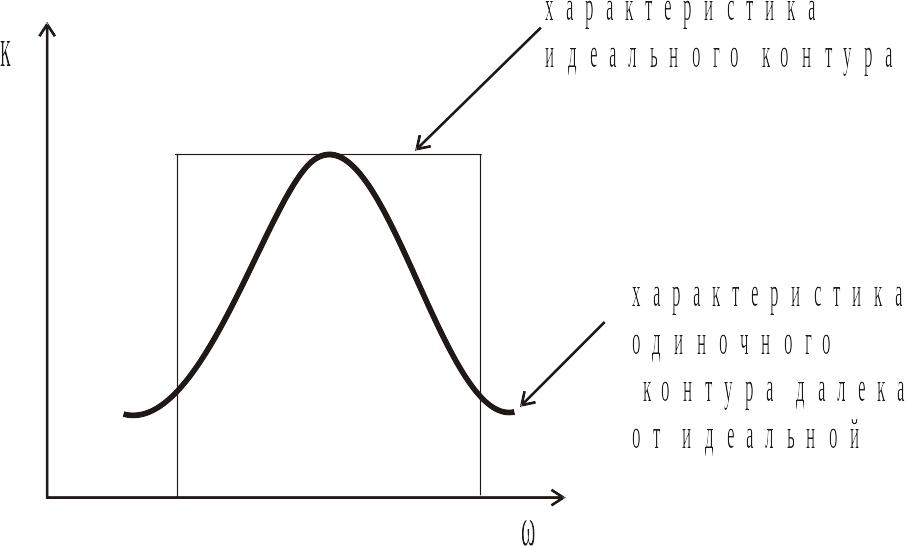
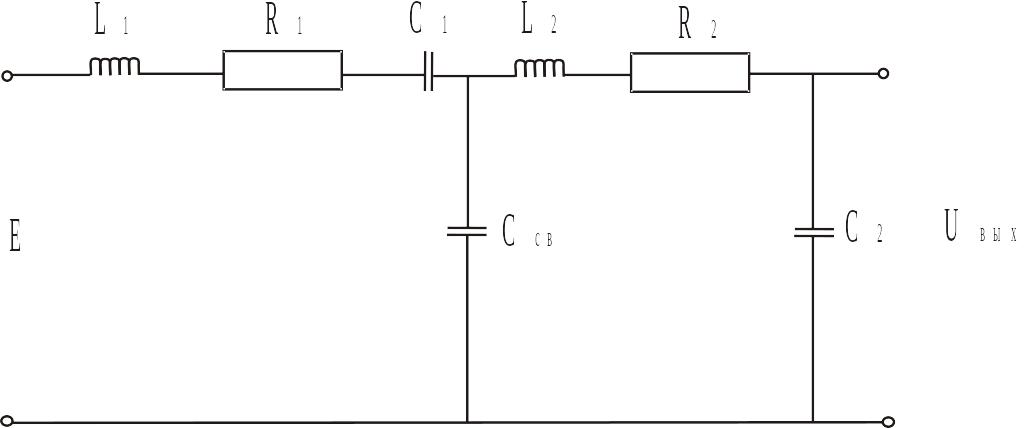
Общий
элемент 2-х контуров - ![]()
Такая связь называется - емкостной.
Связь может быть индуктивной, гальванической , когда общий элемент - резистор.
Связь может быть сложной, когда общий элемент - какие-то схемы.
Вид связи всегда относителен.
Рассмотрим трансформаторную связь (индуктивную).
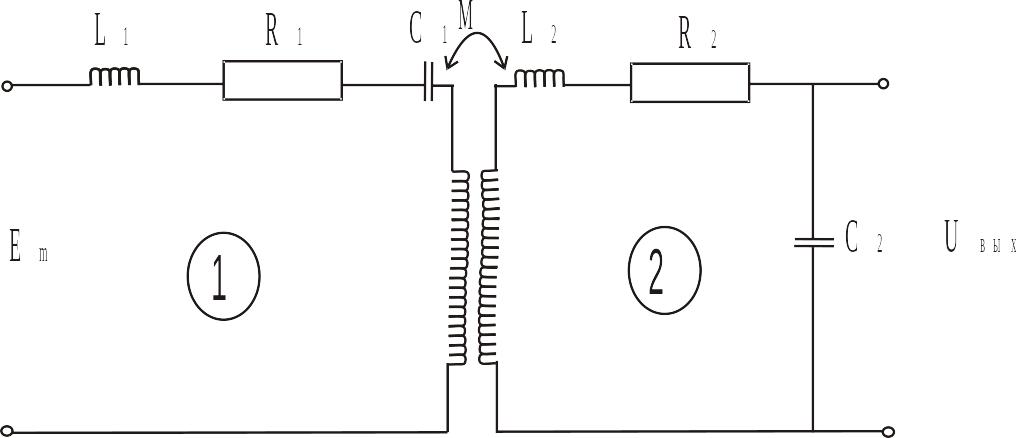
М - коэффициент взаимоиндукции.
ЭДС:
![]() - ЭДС, вносимая из 2-ого контура в 1
- ЭДС, вносимая из 2-ого контура в 1
![]() - ЭДС, вносимая из 1-ого контура во 2-ой
- ЭДС, вносимая из 1-ого контура во 2-ой
Представим
токи в виде: (![]() и
и ![]() )
)
![]() (*)
(*)
(Система уравнений Кирхгофа)
Запишем уравнение в комплексных амплитудах
 Система уравнений с 2 неизвестными
Система уравнений с 2 неизвестными
Решив
систему окажется ![]()
![]() - сопротивление, вносимое из контура
2 в контур 1.
- сопротивление, вносимое из контура
2 в контур 1.
Пусть
![]()
![]()
![]()
![]() - добротность
- добротность ![]()
 - коэффициент связи.
- коэффициент связи.


Свойства схемы определяются величиной æ Q
Рассмотрим случаи:
æ Q <<1 - случай слабой связи.
Обозначим
![]() - коэффициент передачи одиночного
контура, тогда максимальный коэффициент
передачи будет равен:
- коэффициент передачи одиночного
контура, тогда максимальный коэффициент
передачи будет равен:
![]() = Q
- при резонансе
= Q
- при резонансе
В этом случае амплитудно-частотная характеристика имеет вид:
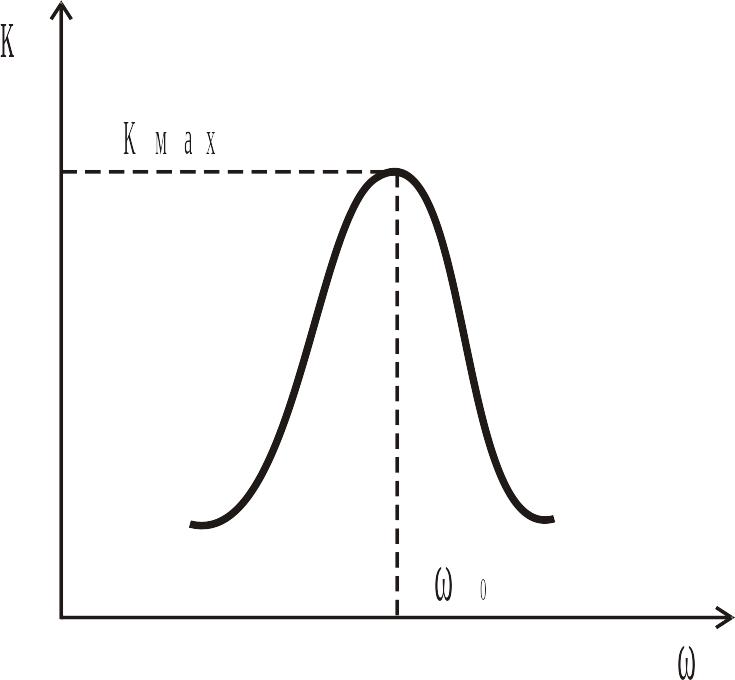
— полоса уже, чем для одиночного контура
æ Q =1 - случай критической связи
коэффициент
передачи: ![]() ;
η =
;
η = ![]() — обобщенная расcтройка
— обобщенная расcтройка
при
резонансе
η=
0, тогда ![]()

Амплитудно-Частотная Характеристика ближе к П-образной.
æ Q >1 Случай сильной связи

Появляются 2 резонансные частоты
У
каждого из одиночных контуров собственная
частота -
, а когда их связывают, при сильной
связи, у них появляется 2 собственные
частоты ![]() - при сильной связи частота расходится
на 2-е.
- при сильной связи частота расходится
на 2-е.

Схемы сложных фильтров :
Полосовой фильтр:

Заградительный фильтр: