Определение мощности
В нашем случае только для активного сопротивления
;
=
– но так мощность нельзя посчитать.
,
где 
- действительная часть, 
- комплексно сопряженное.
Чем
меньше, тем много больше мощность.
Линейный четырехполюсник
Под линейным четырехполюсником понимают устройство с четырьмя зажимами, двумя входными и двумя выходными.
Задача любой линейной цепи является обеспечение функций передачи и фильтрации сигналов в тракте канала связи.
Обозначается:
Пусть на вход подаем -й сигнал. На выходе будет такой же -й сигнал, но может измениться амплитуда с фазой.
,
- все они функции частоты.
Чем характеризуются
полюсники:
-комплексный
коэффициент передачи 
полюсника зависит от частоты (
)
- Амплитудно-частотная характеристика
полюсных. (АЧХ)
-фазочастотная
характеристика
полюсника. (ФЧХ)
Какими должны быть характеристики полюсника, чтобы он не искажал сигнал?
K=K(
Чтобы сигнал не искажался, необходимо чтобы в некотором диапазоне частот ( ширина канала связи) коэффициент передачи
был бы постоянным, а время задержки
не зависело бы от частоты.
; 
Это идеальные характеристики.
Насколько реальные близки к идеальным опред. Допустимыми источниками.
Фильтрующие свойства последовательного контура.
-пример линейного полюсника, который можно использовать в качестве фильтра.
Найдем
коэффициент передачи для этой системы,
равный отношению комплексной амплитуде
напряжения на конденсаторы Аmc
к комплексной амплитуде ЭДС 
;
Если
снимать сигнал с катушки: Если
снимать сигнал с 
:
При
резонансе амплитуда колебаний на
катушке и конденсаторе увеличивается
в 
раз.
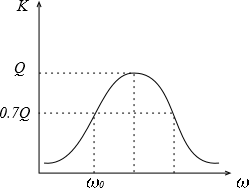
в близи собственной частоты эта характеристика близка к идеальной.
Фазачастотная
характеристика – линейна 
Рассмотренный случай является примером фильтра.
Фильтры служат для разделения токов различных частот, т.е. одни частоты несут информацию, а другие оказывают вредное воздействие.
-обобщенная
расстройка 
резонансная частота контура
- полное сопротивление последовательного
контура
реакт. сопротивление контура
– характеристическое сопротивление
контура
– добротность
2
-
ширина полосы пропускания.
;
;
Напряжение на инд-ти и емкости:
При частоте 
-
резонансной выражение в скобках
обратится в нуль, т.е. при 
,
ток в цепи достаточно меньшего значения:
при этом напряжение на L
и C соответствует:
;
Величина называющая во сколько раз при
резонансе амплитуда этих превышает
амплитуду ЭДС генераторе называется
добротностью
-
затухание.
, где 
-характеризуется сопротивлением
контура.
Классификация фильтров
Фильтры классифицируются по признаку частот, пропускаемых в исследуемую цепь.
Фильтры Низких Частот- ФНЧ
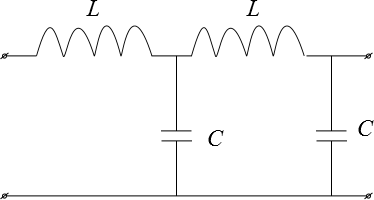
Фильтры Высоких Частот- ФВЧ
Полосовой фильтр –пропускает частоты в некоторой полосе (ПФ)
П
ример
полосового фильтра – последовательный
контур
Заградительный фильтр – пропускает все частоты, кроме некоторой полосы. (ЗФ)
Полосовой Фильтр можно получить как
фильтр высоких частот с 
плюс фильтр низких частот с 
ПФ= ФВЧ +ФНЧ
Фильтр наиболее полно характеризуется зависимостью коэффициента передачи от частоты. Коэффициент передачи мощности сигнала на выходе фильтра и мощности поступающей на вход, удобно оценивать в логарифмической шкале. За единицу отношения мощности принят бел( в честь А.Г. Белла), которая определяется как
,
На практике используются, как правило, (величина в 10 раз меньше) децибелом, коэффициент передачи, выраженный в децибелах:
Из-за квадратичной зависимости мощности
тока (напряжения) коэффициент передачи
тока (напряжения) определяется как: 
Октава - изменение частоты вдвое.
Декада- изменение частоты в 10 раз.