
- •1 Ряди. Властивості збіжних рядів.
- •В ластивості збіжних рядів
- •2 Теореми порівняння
- •3 Ознаки збіжності числових рядів з додатними членами
- •4 Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди, їх властивості.
- •5 Функціональні ряди. Властивості рівномірно збіжних рядів
- •6 Неперервність суми функціонального ряду
- •7 Почленне інтегрування та диференціювання раціональних рівнянь
- •8 Степеневі ряди. Теорема Абеля. Радіус збіжності.
- •9 Почленне дифер. Степ. Рядів. Рівномірна збіжність степеневих рядів.
- •10 Ряд Тейлора. Ряди Маклорена основних елементарних функцій.
- •11 Біоміальний ряд.
- •12 Ряд Фур’є з періодичної функції з періодичної функції.Теор Діріхле.
- •13 Ряд Фур’є для парних і непарних функцій.
- •14 Ряди Фур’є з довільним періодом. Ряд Фур’є функції заданої на дов. Проміжку. Теор. Діріхле.
- •15 Ряд Фур’є в комплексній Формі. Теорема Діріхле.
- •16 Інтеграл Фур’є в тригонометричній формі. Умови збіжності.
- •17 Інтеграл Фур’є в в комплексній формі.
- •18 Перетворення Фур’є в комплексній формі .Sin-,cos- перетворення Фур’є
- •19 Властивості перетворення Фур’є.
- •20 Похідна ф-ції комплексної змінної. Умови Коші – Рімана.
- •21 Геометричний зміст модуля.
- •22 Елементарні функції та їх властивості
- •23 Елементарні функції sinz;cosz;lnz
- •24 Обернено тригон.Функції та їх властивості.
- •25 Інтегра від функції комплексної змінної. Його властивості,формула обчислення(довести 4 власт)
- •26 Інтегральна теорема Коші. Узаг. Теорема коші.
- •27 Інтегр. Ф-ла Коші
- •28 Первісна функції комплексної змінної(довести самост.)
- •29 Ряд Тейлора(фкз). Формула Коші для похідної.
- •30 Ряд Лорана.
- •31 Особливі точки фкз. Їх класифікація.Ряд Лорана в усувн.Т.
- •32 Ряд Лорана в полюсі.
- •33 Лишки, їх обчислення. Обчислення лишків в полюсі. Лишки
- •Теорема Коші
- •34 Перетв Лапласа.Зображення деяких оригіналів
- •Доведення
- •35 Властивості перетворення Лапласа.
- •36 Теорема Бареля
- •37 Формула Рімана – Мелліна.
- •38 Знаходження оригіналів за допомогою лишків.
- •Доведення
- •39 Ітеграл Дюамеля
16 Інтеграл Фур’є в тригонометричній формі. Умови збіжності.
Розглянемо функцію f(x) на проміжку (-l;l). Нехай вона задовольняє умовам Діріхле, тоді:

Підставимо сюди значення коефіцієнтів:
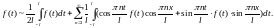

Введемо
позначення:
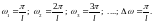
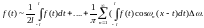
Нехай f(x) – не є періодичною і є інтегрованою на всій числовій прямій:
 Тоді,
перший доданок
Тоді,
перший доданок

Будемо збільшувати l, тоді проміжок (-l;l) розтягнеться на всю числову пряму. Позначимо інтеграл під знаком ряду:

Природньо
вважати, що при
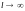 цей ряд перетвориться на інтеграл .
Одержимо:
цей ряд перетвориться на інтеграл .
Одержимо:
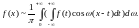
Це інтеграл Фур’є в тригонометричній формі.
Якщо f(x) - інтегрована на R та задовольняє умовам Діріхле на кожному скінченному проміжку, то інтеграл Фур’є збігається в кожній точці до значення:
17 Інтеграл Фур’є в в комплексній формі.
Запишемо інтеграл Фур`є в тригонометричній формі:
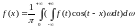
Можна
помітити, що інтеграл в дужках – парна
функція відносно
 ,
бо
-
під знаком cos. Це значить, шо формулу
можна записати у вигляді:
,
бо
-
під знаком cos. Це значить, шо формулу
можна записати у вигляді:
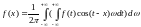
 -
непарна відносно
,
звідси
-
непарна відносно
,
звідси
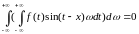
Помножимо
остаточний інтеграл на число
 і додамо до інтеграла Фур`є:
і додамо до інтеграла Фур`є:
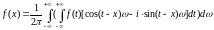
За формулою Ейлера
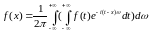

Назвемо функцію
 -
перетворення
Фур`є
-
перетворення
Фур`є
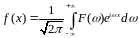 -
обернене
перетворення Фур`є
-
обернене
перетворення Фур`є
Іноді перетаоренням Фур’є називають функцію
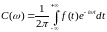 -
спектральна характеристика.
-
спектральна характеристика.
Функція
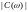 називається
амплітудно-частотним спектром.
називається
амплітудно-частотним спектром.
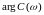 -
фазо-частотний спектр.
-
фазо-частотний спектр.
В інших позначеннях :
Амплітудно-частотний
спектр -
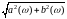
Фазо-
частотний спектр -
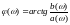 .
.
Ці функції можуть відрізнятись коефіцієнтами.
18 Перетворення Фур’є в комплексній формі .Sin-,cos- перетворення Фур’є
Згадаємо формулу Ейлера
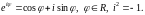

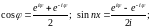
Підставимо ці формули в ряд Фур’є:
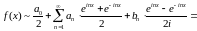

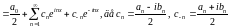 (1)
(1)
Знайдемо вирази для комплексних коефіцієнтів:

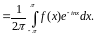
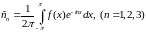
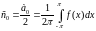
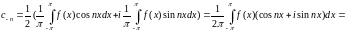
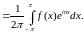
Таким чином, формулу (1) можна записати:
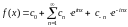 ,
або
,
або
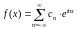 (2)
(2)
Коефіцієнти цього ряду можна записати:
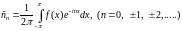 (3)
(3)
Рівність
(2) називається комплексною формою ряду
Фур’є
функції f(x),
а
число
 ,
знайдене за формулою (3) - комплексними
коефіцієнтами ряду Фур’є.
,
знайдене за формулою (3) - комплексними
коефіцієнтами ряду Фур’є.
Якщо
функція f(x),
задається
на відрізку
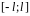 ,
то комплексна форма її ряду Фур’є має
вигляд:
,
то комплексна форма її ряду Фур’є має
вигляд:
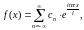

Формулу Фур’є можна представити в симетричній формі запису:
 ,
,

У випадку парної функції:
 де
де
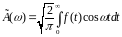
У випадку непарної функції:
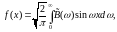
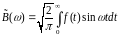
Функції
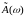 і
і
 називають
відповідно косинус-перетвореннями і
синус-перетвореннями Фур’є для функції
f(x).
називають
відповідно косинус-перетвореннями і
синус-перетвореннями Фур’є для функції
f(x).
19 Властивості перетворення Фур’є.
1) Лінійність
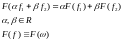
2)

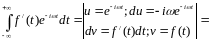
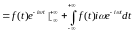
Знайдемо 1-й доданок
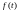 інтегрована
на R,
інтегрована
на R,
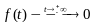
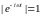 ,
,
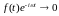 при
при

За допомогою перетворення Фур’є можна розв’язувати диференційні рівняння тому, що взявши перетворення Фур’є від лівої та правої частини рівняння ми одержимо лінійні рівняння відносно функції F. Знайшовши функцію F, знаходимо f.
3)

4)

5)

20 Похідна ф-ції комплексної змінної. Умови Коші – Рімана.
Теорема:
Похідна
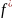 (z)
шснує в т.
(z)
шснує в т.
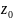 ,
тоді і тільки тоді, коли U(x;y),
V(x;y)
диференц. В цій точці та зв’язані двома
рівностями:
,
тоді і тільки тоді, коли U(x;y),
V(x;y)
диференц. В цій точці та зв’язані двома
рівностями:
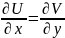 ці
рівності називаються умовами Коші-Рімана.
ці
рівності називаються умовами Коші-Рімана.
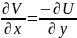
f(z)=U+iV Доведення:
Нехай
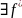 (
)
=
(
)
=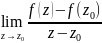 За властивістю границь:
За властивістю границь:
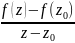 =
(
=
(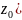 +
+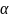 ,
,
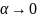 при
при
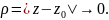 Тоді помноживши ліву і праву частини
на знаменник:
Тоді помноживши ліву і праву частини
на знаменник:
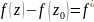 (
)
(
)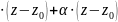 (1)
(1)
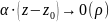 неск.
мала більш високого порядку, ніж
неск.
мала більш високого порядку, ніж

Нехай f(z)=U+iV
( )=A+Bi z=x+iy
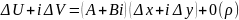 (2)
(2)
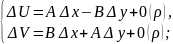 (3)
(3)
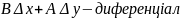
Оскільки
за умовою U
і V
– диференційовані, то з першої рівності
випливає:
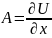 ;
;
З
другої рівності випливає:
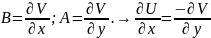
Нехай виконується умова Коші-Рімана:
;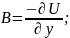 Тоді має місце система (3). Другу рівність
(3) помножимо на i
й
додамо до першої. Вийде рівність (2).
Тоді має місце система (3). Другу рівність
(3) помножимо на i
й
додамо до першої. Вийде рівність (2).
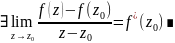
Зауваження: У диференц. функцій f(z), U і V-жорстко зв’язані, тобто якщо задати U, то V знаходиться точно за константою (і навпаки).
Наприклад: Задано U(x;y). Знайдемо функцію V(x;y), щоб функція V(z) була диференційована.
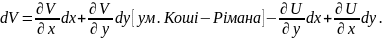
Щоб знайти невідому функцію V необхідно розглянути інтеграл другого роду:
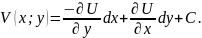
Якщо
задано V,
то
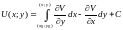 .
.
Зауваження. Якщо f’(z) існує, то її можна знайти за однією із формул:
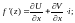
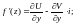

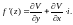
Зауваження. Якщо U і V зв’язані умовами Коші-Рімана, то вони обов’язково будуть гармонічними:

U - гармонічна.
Така пара функцій U і V, яка зв’язана умовами Коші-Рімана називається гармонічно-спряженими функціями.
