Шпора (Вишка)

1. Визначники другого та третього порядку їх властивості.

Детермінантом або визначником другого порядку квадратної матриці називають вираз .

Визначники n-ого порядку, означення.

Властивості ті ж самі, що і в першому питанні. Визначники квадратної матриці, що складається з n^2 елементів, називається алгебраїчна сума n! доданків, кожен доданок є добутком n-доданків взятих по одному з кожного рядка і кожного стовпчика квадратної матриці і помножених на (-1)^t де t – це число інверсії в других індексах, якщо елементи доданку розташовані в порядку зростання перших індексів.

Визначник 3-го порядку

Властивості.

1. Визначник не змінюються, якщо рядки поміняти місцями зі стовпчиками.

2. Якщо поміняти місцями два рядки він поміняє знак.

3. Якщо всі елементи ряжка у визначнику = 0, то визначник = 0.

4. Визначник, що містить два однакових рядки = 0.

5. Якщо всі елементи деякого рядка мають спільний множник, то цей множник можна винести за знак множника.

6. Визначник, який містить пропорційні рядки, дорівнює 0.

7. Якщо елементи деякого рядка є сумою двох доданків, то визначник дорівнює сумі двох визначників.

8. Якщо до елементів деякого рядка додати елементи іншого рядка, помножені на одне й те саме число, то визначник не зміниться.

2. Елементарні перетворення матриць. Застосування.

• транспонування матриці (заміна рядків стовпчиками. А стовпчиків рядками)

• перестановка місцями рядків чи стовпчиків

• множення елементів рядка на відмінне від 0 число.

• викреслення одного чи кількох рядків з пропорційними елементами.

• викреслення нульових елементів чи стовпчиків

• додавання до рядка інший рядок помножений на деяке

число.

5. Ранг матриці та його властивості.

Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.

r(A)=rank A= rang A

Властивості.

• r(A)n,m

• ранг нульової матриці дорівнює нулю

• Якщо А квадратна матриця, n=m, det(a)0, r(a)=n

Якщо r(A)=r, то всі мінори порядку вище ніж r дорівнюють 0

Способи обчислення рангу матриці.

• спосіб обвідних мінорів

Вибираємо М₂ , складаються мінори третього порядку , що місять цей мінор. Якщо всі мінори 3-го порядку = 0, тоді ранг = 2. Якщо хоча б один мінор 3-го порядку , повторюємо те саме.

• спосіб елементарних перетворень.(до трапецеп. матриці).

Ранг трапецеподібної матриці = max числу її ненульових рядків.

9. Системи лінійних алгебраїчних рівнянь. Правило Крамера.

n-рівнянь і m-невідомих. Система називається сумісною, якщо існують такі х1=в1, х2=в2, …, х_м=в_м,які при підстановці в систему задовольняють всі рівняння. Сукупність таких значень називають розв’язком системи.

Однорідна система (всі частки системи дорівнюють 0) завжди сумісна.

6. Метод Гаусса.

Зводимо до трапецеподібної форми. Якщо потрібно, вводимо константи. Перетворюємо матрицю назад в систему. Обчислюємо систему.

Теорема Кронекера-Капеллі.

Система однорідних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці системи = рангу розширеної. Система має єдиний розв’язок, якщо ранг = кількості невідомих і безліч, якщо ранг < кількості невідомих.

30. Поняття Функції.

Якщо для кожного x є X за визначеним правилом вибраний елемент y є Y, то кажуть, що задана функція(відображення) f множини X в множину Y, при цьому пишуть f: XY.

Елемент х є Х назив. аргументом функції, елемент у є Y – значенням функції, відповідним елементу х є Х, y = f(x), а сама ф-ція є правилом, що перероблює кожний х є Х в y = f(x).

Множина Х назив. областю визначення ф-ції, а множина всіх елементів у є Y, для яких існують х є Х такі, що f(x) = y – множиною значень ф-ції f.

4. Обернені матриці. Правило обчислення і властивості обернених матриць.

Якщо А – квадратна матриця, то матриця А^-1 називається оберненою до А, якщо А^-1*A=A*A^-1=E.

Щоб квадратна матриця А мала обернену необхідно і достатньо, щоб вона була невиродженою, тобто щоб її визначник не дорівнював 0.

Властивості оберн. матриць:

12, 13. Умови колінеарності та компланарності.

Вектори a і b називаються колінеарними, якщо вони лежать на одній або паралельних прямих.

Три вектори a, b, c називаються компланарними, якщо вони лежать в одній або паралельних площинах, зокрема якщо хоча б 2 із 3-ох векторів колінеарні, або хоча 1 є нуль-вектором.

10. Вектори на площині і у просторі. Основні поняття.

Геометричним вектором називається напрямлений відрізок прямої. Довжину цього відрізка називають модулем або довжиною вектора. Задати вектор означає вказати його довжину і напрям. Вектор довжина якого дорівнює нулю називається нуль-вектором. Напрям нуль-вектора не заданий. Вектори назив. рівними, якщо вони мають однакову довжину і напрям.

Вектор довжина якого = 1 назив. одиничним. Одиничний вектор співнапрямлений вектору а назив. ортом. Оскільки геометричні вектори можна переміщувати по площині, то їх називають вільними.

Кутом між векторами а і b зведеними до спільного початку назив. найменший кут на який треба повернути вектор a , щоб напрями a і b співпали. Поворот проти годинникової стрілки вважається додатнім.

Кути між вектором та координатними осями О_х та О_у назив. напрямленими, а cos цих кутів напрямленими косинусами.

На площині напрямлені cos пов’язані співвідношенням cos^2+cos^2=1.

Вектори на площині і лінійні операції над векторами, їх властивості.

1. Добутком дійсного числа  на вектор  назив. новий вектор довжина якого дорівнює довжині вектора  помноженого на модуль числа , а напрямок співпадає з напрямком вектора , якщо >0, і протилежно напрямлений, якщо <0.

2. Сумою векторів  називають такий вектор c, у якого початок співпадає з початком вектора , а кінець співпадає з кінцем вектора , за умови, що початок вектора  співпадає з кінцем вектора 

Різницею  назив. такий вектор c, напрямлений з кінця вектора  в кінець вектора , за умови, що початки векторів і співпадають.

Властивості:

14. Скалярний добуток векторів, його властивості.

Скалярним добутком векторів a і b називають число, що дорівнює добутку модулів a і b на косинус кута між ними.

Властивості:

Вектори a і b перпендикулярні тоді, коли їх скалярний добуток дорівнює 0. Якщо хоча б один з векторів є нуль-вектором, то скалярний добуток = 0.

11. Базис

Будь-яка пара впорядкованих неколінеарних векторів утворює базис.

i,j – ортонормований базис. Нехай a=(Xa,Ya) b=(Xb,Yb), то ці вектори будуть утворювати базис за умови Xa/XbYa/Yb.

Теорема: Якщо вектори E₁ та E₂ утворюють базис, то будь-який третій вектор можна подати у вигляді лінійної комбінації двох перших векторів. a=X₁E₁+X₂E₂ a(X₁, X₂)

Таке представлення вектора а називається розкладом його за базисом E₁ та E₂.

Теорема2. Розклад за базисом єдиний

26. Властивості збіжних послідовностей. Теорема про суму збіжних послідовностей. Послідовність, що має скінчену границю назив. збіжною. Якщо границя не існує або нескінченна, послідовність назив. розбіжною.

Нехай послід. збіжні і мають відповідні границі: . Тоді існують границі таких послід-ей:

1.

Оскільки , це означає, що для Оскільки , це означає, що для

;

28, 27. Нескінченно малі і нескінченно великі.

Ф-ція назив. НВ при , якщо

Ф-ція назив. НВ при , якщо

Ф-ція назив. НМ при , якщо

Властивості НМ:

1. Скінчена сума НМ ф-цій при є НМ.

2. Добуток НМ на обмежену ф-цію є НМ.

3. Добуток скінченого числа НМ ф-цій є НМ.

4. Якщо f(x) – НМ, , то 1 / f(x) - НВ, .

. Доведення: Розгл. коло радіуса R.

S(три-ка OAC)<S(сектораOAC)<S(три-каOAB)

; ;

; ; ;

. Наслідки:

36. Друга визначена границя. Її наслідки.

Доведення.Нехай x>1, , тоді знайдеться n є N, що n x < n+1. N=[x]-ціла част. х.

1-й і 3-й вирази наближаються до e,n і до нескінченності. Отже і 2-й теж до e.

Наслідки:

37. Порівняння НМ.

НМ одного порядку малості позначають x(x)), x прямує до a.

, xє НМ більш високого порядку малості, ніж (x).

, навпаки.

. Еквівалентні.

38. Еквівалентність нескінчено малих. Необхідна і достатня умова еквівалентності.

Теж саме з f(x) замість x. Теорема: у відношеннях та добутках НМ ф-цій під знаком lim можна змінювати на еквівалентні їм ф-ції.

Доведення:

;

Алгебраїчна сума НМ різного порядку малості еквівалентна НМ найменшого порядку малості.

31. Неперервність.

f(x) наз. неперервною у т. x₀ якщо:

1. Вона визначена у т. х. 2. Існує границя ф-ції у цій точці.

3. lim f(x)=f(x ₀) х прямує до х ₀.

За Коші. Ф-ція неперервна у т. х₀ якщо

f(x) назив. неперервною у т. х₀, якщо НМ приросту аргументу відповідає НМ приріст ф-ції.

f(x) наз. неперервною у т. х₀, якщо

31. Властивості неперервних.

Якщо f(x), g(x) – неперервні, то

. теж неперервні.

Якщо ф-ція x=t неперервна у т. t₀ ? а f(x) – неперервна у т. х₀=t то f((t)) тепер у т. t₀.

Теорема про неперервність оберненої ф-ції: y=f(x) неперервна у т. x₀ є x - числ. множина і надій множині існ. оберн. ф-ція x=f^-1(y) , то ця ф-ція є неперервною у т. y₀; y₀=f(x₀).

32. Точки розриву та їх класифікація.

Точки у яких ф-ція не існує або не визначена назив. точк. розриву.

1. . Розрив типу стрибка.

2. х₀ - т. усувного розриву.

3. Якщо одна з одностор. Границь не існує, або = нескінч. у т. х₀ , то х₀ – точка розриву 2-го порядку.

34. Функції неперервні на відрізку.

Ф-ція назив. неперервною на відрізку ab, якщо вона неперервна в кожній точці цього відрізку причому f(a+)=f(a), f(b-)=f(b).

1 теорема Вейерштрасса: Ф-ція неперервна на відрізку є обмеженою на цьому відрізку.

2 теорема Вейерштрасса:

Неперервна на відрізку ab ф-ція, набуває на цьому відрізку свого найбільшого значення.

1 теорема Бальцано-Коші: Якщо ф-ція неперервна на відрізку і на кінцях відрізка набуває протилежних знаків, то на відрізку існує хоча б 1 точка, в якій ф-ція вертається в “0”.

2 теорема Бальцано-Коші: Якщо ф-ція неперервна на відрізку і набуває на ньому свого max і min то вона набуває на відрізку і всі проміжні значення

39. Поняття похідної ф-ції.

Границя відношення приросту ф-ції до приросту аргументу, коли приріст аргументу прямує до нуля, назив. похідною ф-ції у т. х.

Геометричний зміст похідної.

- р-ня дотичної у т. х₀.

Пряма перпендикулярна до дотичної у т. х₀ назив. нормаллю.

44. Похідна складеної і оберненої ф-цій.

Т1. Нехай ф-ція х=tдифер. у т. t, а ф-ція y=f(x) – диференційована у т. х₀=t₀, тоді ф-ція y=f((x)(t)) – дифер. у т.t₀.

Наслідок:

Т2. Якщо ф-ція y=f(x) дифер. у т. х₀ - дифер у т. y₀=f(x₀).

48. Похідні ф-цій, що задані неявно і параметрично.

Якщо ф-ція задана р-ням y=f(x) розв’язаним відносно y , то кажуть, що ф-ція задана явно. Якщо ф-ція задана р-ням F(x;y)=0 не розв. Відносно y , то кажуть, що ф-ція задана неявно. Щоб знайти похідну неявної ф-ції необхідно взяти похідну за змінною х від рівності F(x;y)=0 пам’ятаючи, що y – є ф-ція від х, а потім розв. р-ня відносно похідної y. Похідна буде виражаится через змінні х та y.

Якщо ф-ціональна залежність між х та y задається рівнянням:

, t – належить одному й тому ж проміжку, то кажуть що ф-ція задана параметрично. Якщо y=t строго монотонна, то існує обернена ф-ція і y можна записати у вигляді . Похідна: =

=

Правило Лопіталя.

Т1. Нехай ф-ції f(x), g(x) – дифер. в околі х₀. ,

у т. х₀ тоді якщо

то

Т2. Якщо ф-ція f(x), g(x) дифер. в околі т. х₀ і і то

30. Поняття вищих порядків. Тейлор та Маклорен.

- друга похідна. Похідна від другої – третя..

Похідною n–го порядку ф-ції f(x) на інтервалі (a,b) назив. першу якщо вона існує від похідної n–го порядку. Похідні порядку вище першого назив. похідн. вищих або старших порядків.

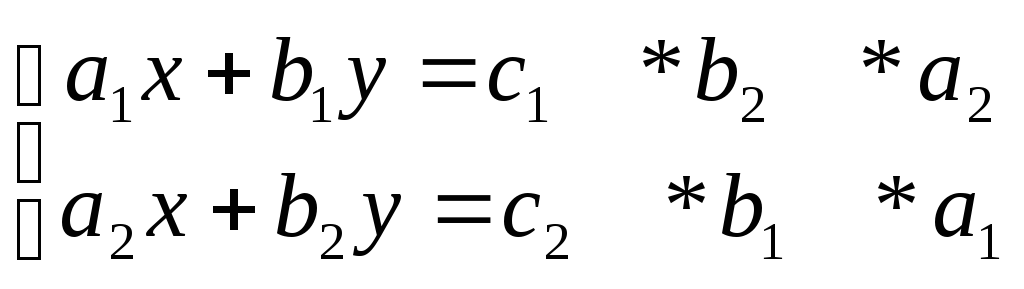
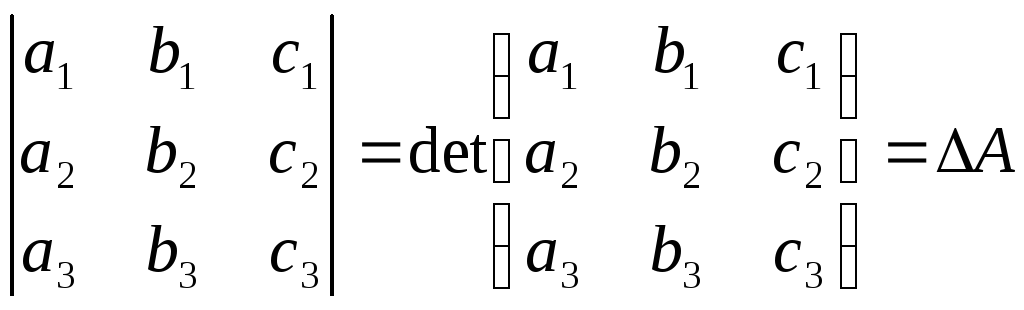
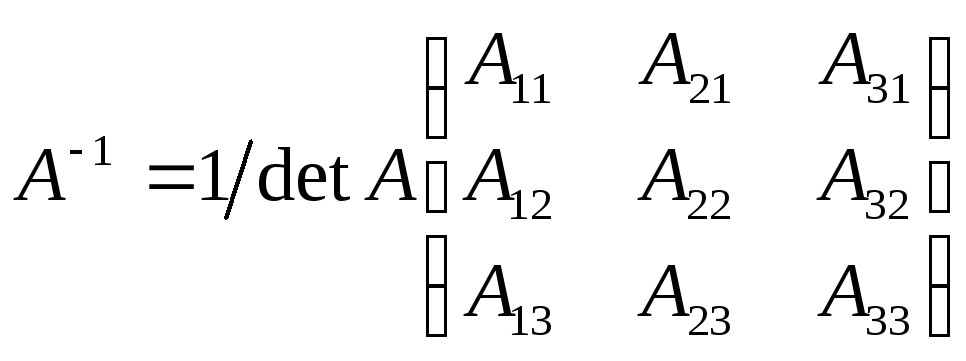
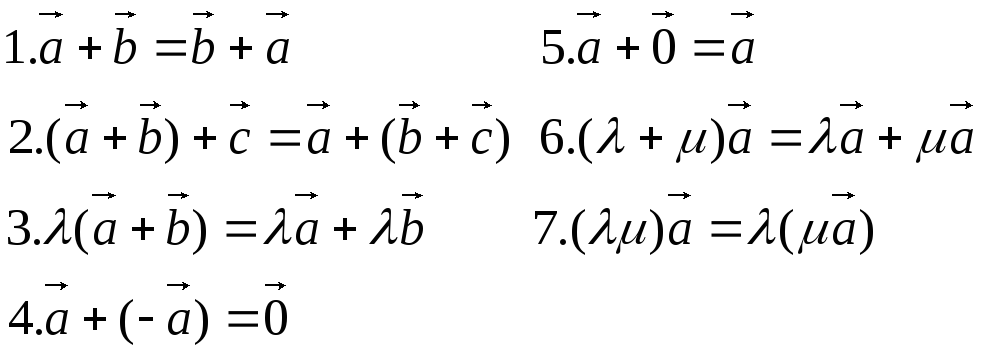
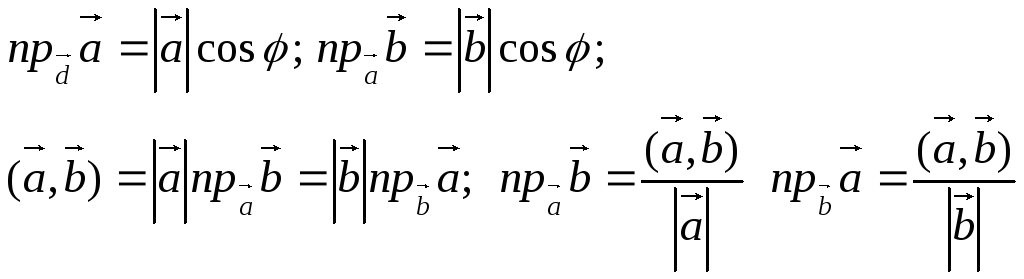
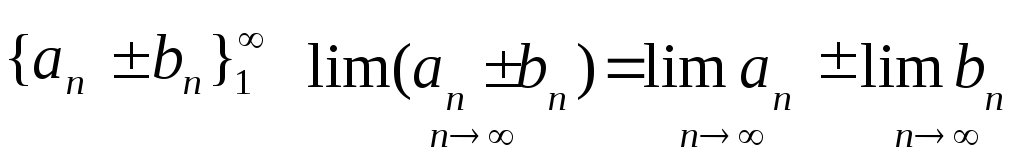
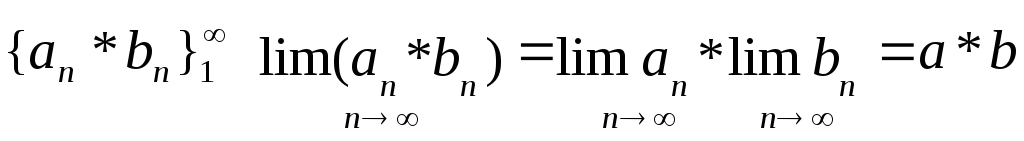
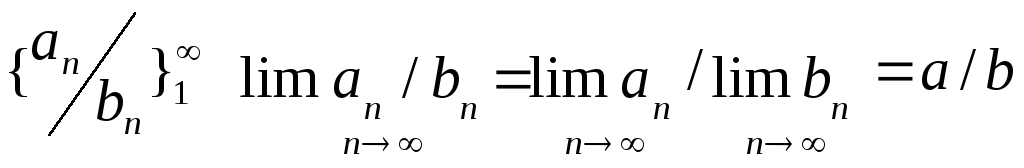
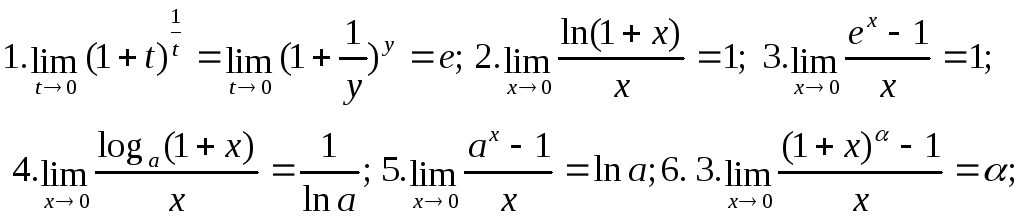
Ф-ла Тейлора. Нехай ф-ція дифер. в околі т. х₀ і має похідні (n+1)-порядку, x є околу т. х₀, тоді є така т. с що лежить між х і х₀ і ф-л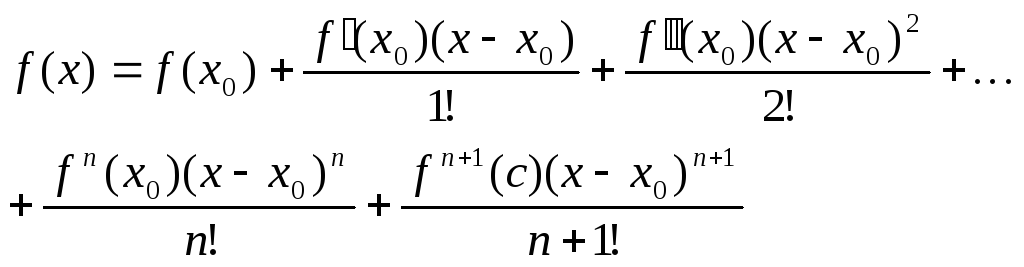а: Останній доданок – залишковий член, а все інше – “многочлен Тейлора”. При x₀ ф-ла назив. Маклорена.