
- •1 Ряди. Властивості збіжних рядів.
- •В ластивості збіжних рядів
- •2 Теореми порівняння
- •3 Ознаки збіжності числових рядів з додатними членами
- •4 Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди, їх властивості.
- •5 Функціональні ряди. Властивості рівномірно збіжних рядів
- •6 Неперервність суми функціонального ряду
- •7 Почленне інтегрування та диференціювання раціональних рівнянь
- •8 Степеневі ряди. Теорема Абеля. Радіус збіжності.
- •9 Почленне дифер. Степ. Рядів. Рівномірна збіжність степеневих рядів.
- •10 Ряд Тейлора. Ряди Маклорена основних елементарних функцій.
- •11 Біоміальний ряд.
- •12 Ряд Фур’є з періодичної функції з періодичної функції.Теор Діріхле.
- •13 Ряд Фур’є для парних і непарних функцій.
- •14 Ряди Фур’є з довільним періодом. Ряд Фур’є функції заданої на дов. Проміжку. Теор. Діріхле.
- •15 Ряд Фур’є в комплексній Формі. Теорема Діріхле.
- •16 Інтеграл Фур’є в тригонометричній формі. Умови збіжності.
- •17 Інтеграл Фур’є в в комплексній формі.
- •18 Перетворення Фур’є в комплексній формі .Sin-,cos- перетворення Фур’є
- •19 Властивості перетворення Фур’є.
- •20 Похідна ф-ції комплексної змінної. Умови Коші – Рімана.
- •21 Геометричний зміст модуля.
- •22 Елементарні функції та їх властивості
- •23 Елементарні функції sinz;cosz;lnz
- •24 Обернено тригон.Функції та їх властивості.
- •25 Інтегра від функції комплексної змінної. Його властивості,формула обчислення(довести 4 власт)
- •26 Інтегральна теорема Коші. Узаг. Теорема коші.
- •27 Інтегр. Ф-ла Коші
- •28 Первісна функції комплексної змінної(довести самост.)
- •29 Ряд Тейлора(фкз). Формула Коші для похідної.
- •30 Ряд Лорана.
- •31 Особливі точки фкз. Їх класифікація.Ряд Лорана в усувн.Т.
- •32 Ряд Лорана в полюсі.
- •33 Лишки, їх обчислення. Обчислення лишків в полюсі. Лишки
- •Теорема Коші
- •34 Перетв Лапласа.Зображення деяких оригіналів
- •Доведення
- •35 Властивості перетворення Лапласа.
- •36 Теорема Бареля
- •37 Формула Рімана – Мелліна.
- •38 Знаходження оригіналів за допомогою лишків.
- •Доведення
- •39 Ітеграл Дюамеля
4 Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди, їх властивості.
Означення: Ряд називається знакозмінним, якщо серед його членів є як невід’ємні, так і від’ємні числа.
Зауваження: Якщо серед членів ряду є лише скінченна кількість членів одного із знаків, то такий ряд може розглядатися як ряд з додатними членами. Шляхом розгляду окремо його членів до певного номера та після нього.
Теорема Лейбніца:
Нехай члени знакозмінного ряду прямують до нуля, складаючи при цьому спадну за абсолютною величиною послідовність, тоді такий ряд є збіжний.
Доведення:
Розглянемо
ряд
;
 ;
;
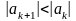 ,
припустимо, що додатними є члени ряду
з непарними номерами a1,
a3,
a5,...;
а від’ємними – члени ряду з парними
номерами:
a2,
a4,
a6,...
.
,
припустимо, що додатними є члени ряду
з непарними номерами a1,
a3,
a5,...;
а від’ємними – члени ряду з парними
номерами:
a2,
a4,
a6,...
.
Розглянемо частинні суми окремо з парними і окремо з непарними номерами:
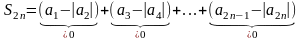 ,
отже у випадку частинних сум з парними
номерами ми маємо зростаючу послідовність,
в той же час
,
отже у випадку частинних сум з парними
номерами ми маємо зростаючу послідовність,
в той же час
 ,
тобто ця послідовність обмежена зверху,
і, відповідно, прямує до певної границі:
,
тобто ця послідовність обмежена зверху,
і, відповідно, прямує до певної границі:
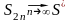 .
Оскільки
.
Оскільки
 то
то
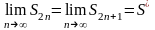 .
.
Знакозмінний ряд називається абсолютно збіжним, якщо збіжним є ряд складений з абсолютних величин його членів.
Тобто,
якщо
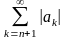 - збіжний, то,
- збіжний, то,
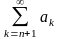 - абсолютно збіжний.
- абсолютно збіжний.
Зауваження: Абсолютно збіжний ряд завжди є збіжний, але не кожен збіжний ряд є збіжний абсолютно. Якщо ряд є збіжний, проте не абсолютно, то такий ряд називається умовно збіжним.
Дійсно
при абсолютній збіжності
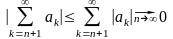
5 Функціональні ряди. Властивості рівномірно збіжних рядів
Нехай
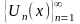 послідовність функцій. Якщо при
фіксованому значенні числова послідовність
послідовність функцій. Якщо при
фіксованому значенні числова послідовність
 є збіжною до числа
є збіжною до числа
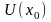 ,
то кажуть, що число х0
належить області збіжності вказаної
послідовності.
,
то кажуть, що число х0
належить області збіжності вказаної
послідовності.
Якщо
по заданій функціональній послідовності
побудовано функціональний ряд
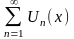 ,
то область збіжності Послідовності
його частинних сум
,
то область збіжності Послідовності
його частинних сум
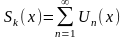 ,
називається областю збіжності цього
ряду.
,
називається областю збіжності цього
ряду.
Означення:
Функціональний ряд називається рівномірно
збіжним на деякому інтервалі
 до функції
до функції
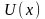 .
Якщо для будь-якого
знайдеться
.
Якщо для будь-якого
знайдеться
 таке, що для будь-якого
таке, що для будь-якого
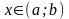 при
при
 виконується нерівність
виконується нерівність
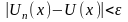 або
або
 .
.
Нехай
для ряду
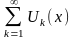 існує збіжний числовий ряд
,
такий що при всіх значеннях k
і довільних x
з інтервалу
виконується нерівність:
існує збіжний числовий ряд
,
такий що при всіх значеннях k
і довільних x
з інтервалу
виконується нерівність:
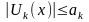 ,
тоді функціональний ряд збігається
рівномірно для
.
,
тоді функціональний ряд збігається
рівномірно для
.
Доведення:
Функціональний ряд є абсолютно збіжним на вказаному інтервалі, оскільки ряд складений з абсолютних величин його членів збігається на цьому інтервалі за мажорантно-мінорантною ознакою порівняння.
2.
Для
будь-якого
,
знайдеться
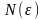 таке, що при
таке, що при
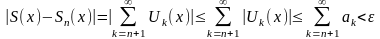 ,
що і означає його рівномірну збіжність.
,
що і означає його рівномірну збіжність.
6 Неперервність суми функціонального ряду
Якщо члени функціонального ряду є неперервними функціями на деякому інтервалі і ряд рівномірно збігається на цьому інтервалі, то його сума неперервна на цьому ж інтервалі.
Доведення: Очевидно, що Sn(x) неперервна на [a;b]. Розглянемо приріст суми ряду: ∆S(x)=∆Sn(x)+∆rn(x); |∆S(x)|≤|∆Sn(x)|+|∆rn(x)|;
оскільки
Sn(x)
неперервна, то
ε<0
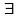 δ>0:
|∆x|<
δ => |∆Sn(x)|<ε/3
δ>0:
|∆x|<
δ => |∆Sn(x)|<ε/3
|∆r(x)|≤|rn(x+∆x)-rn(x)|≤|rn(x+∆x)|+|rn(x)|. З рівномірної збіжності ряду випливає, що для того ж самого ε>0 N(ε): n>N => |rn|<ε/3,
отже |∆S(x)|<ε/3+ ε/3+ ε/3.
