6.Графическое решение задачи линейного программирования (нахождение минимума целевой функции).

На этом шаге мы рассмотрим применение метода графического решения задач линейного программирования для случая минимизации целевой функции.

    Задача "диеты"

    Фармацевтическая фирма ежедневно производит не менее 800 кг некой пищевой добавки, которая состоит из смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.

Таблица 1. Данные задачи "диеты"
Мука	Белок, кг на кг муки	Клетчатка, кг на кг муки	Стоимость (руб./кг)
Кукурузная	0,09	0,02	0,3
Соевая	0,6	0,06	0,9

    Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма хочет определить рецептуру смеси наименьшей стоимости с учетом требований диетологов.

    Поскольку пищевая добавка состоит только из кукурузной и соевой муки, переменными для этой задачи, очевидно, будут x₁ — количество (в кг) кукурузной муки, используемой в дневном производстве пищевой добавки; х₂ — количество (в кг) соевой муки, используемой в дневном производстве пищевой добавки.

    Целевая функция равна обшей стоимости пищевой добавки, производимой за один день, и должна быть минимальной. В данном случае это можно записать следующим образом:

    Минимизировать z = 0,3 x₁+ 0,9x₂.

    Ограничения модели должны отражать производственные требования и рекомендации диетологов. Фирма должна выпускать не менее 800 кг смеси в день.Соответствующее ограничение будет записано следующим образом: x₁+ x₂ ≥ 800.

    Рассмотрим ограничение, связанное с количеством белка в пищевой добавке. Общее количество белка в смеси, состоящей из х₁ кг кукурузной муки и х₂ кг соевой муки, равно 0.09x₁ + 0.6х₂ (кг). Это количество должно составлять не менее 30% от общего объема смеси х₁ + х₂. Отсюда получаем следующее неравенство

0.09х₁ + 0.6x₂ ≥ 0.3(x₁ + х₂).

    Аналогично строится ограничение для клетчатки:

0.02x₁ + 0.06х₂ ≤ 0.05(х₁ + х₂).

    В последних двух неравенствах переменные x₁ и х₂ надо перенести из правых частей неравенств в левые. Окончательно модель примет следующий вид:

Минимизировать z = 0.3x₁ + 0.9x₂ при ограничениях x₁ + x₂ ≥ 800, 0.21х₁ - 0.3x₂ ≤ 0, 0.03x₁ - 0.01x₂ ≥ 0, x₁, x₂ ≥ 0.

    На рис. 1 показано графическое решение этой задачи.

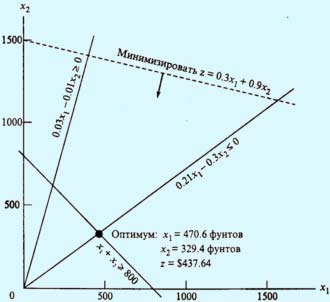Рис. 1. Графическое решение задачи минимизации

    Поскольку в данной модели следует минимизировать целевую функцию, поэтому нужно идти в направлении уменьшения ее значений (это направление на рис. 1 показано стрелкой). Оптимальное решение находится на пересечении прямых x₁ + х₂ = 800 и 0.21x₁ - 0.30x₂ = 0, откуда получаем х₁ = 470.59 (кг) и х₂ = 329.41 (кг). При этих значениях переменных минимальная стоимость производимой ежедневно пищевой добавки составляет z = 0.3 * 470.59 + 0.9 * 329.41 = 437.65 руб.

7.Дополнительные переменные

Введем два типа дополнительных неотрицательных переменных (назовем их остаточными и избыточными, которые связаны с неравенствами, типа "≤" и "≥" соответственно. Введем также понятие свободной переменной, которая может принимать как положительные, так и отрицательные значения (и, конечно, значение 0).

    Остаточная переменная. Неравенства типа "≤" обычно можно интерпретировать как ограничения на использование некоторых ресурсов (представленных в левой части неравенств переменными модели). В такой интерпретации остаточная переменная показывает количество неиспользованных ресурсов. В примере с компанией "Русские краски" неравенство 6x₁ + 4х₂ ≤ 24 связано с использованием сырья M1.

    Это неравенство эквивалентно равенству 6x₁ + 4х₂ + s₁ = 24, где s₁ ≥ 0. Здесь остаточная переменная s₁ (= 24 - 6x₁ - 4х₂) равна неиспользуемому количеству сырья Ml.

    Избыточная переменная. Неравенство типа "≥" показывает, что "что-то" должно быть не меньше определенной величины. Избыточная переменная определяет превышение значения левой части неравенства над этой величиной.

    Например, в модели "диеты" неравенство x₁ + х₂ ≥ 800 показывает, что суточное производство пищевой добавки не должно быть меньше 800 кг. Математически это неравенство эквивалентно равенству x₁ + х₂ – S₁ = 800, где S₁ > 0. Положительное значение избыточной переменной S₁ показывает превышение суточного производства добавки над минимальным значением в 800 кг.

    Свободная переменная. В приведенных выше примерах условие неотрицательности переменных является естественным. Но, конечно, возможны ситуации, когда переменные могут принимать любые действительные значения. Такая ситуация показана в следующем примере.

   Пример 1. Ресторан быстрого обслуживания торгует порционными мясными пирогами и чизбургерами. На порцию мясного пирога идет четверть кг мяса, а на чизбургер — только 0.2 кг. В начале рабочего дня в ресторане имеется 200 кг мяса, можно еще прикупить мясо в течение дня, но уже с наценкой в 25 руб. Мясо, оставшееся в конце рабочего дня, жертвуется благотворительной организации. Ресторан имеет доход 20 руб. от одной порции мясного пирога и 15 руб. — от одного чизбургера. Как и многие другие, этот ресторан не может продать в день более 900 бутербродов. Какова должна быть доля каждого из бутербродов (т.е. сколько порций мясного пирога и сколько чизбургеров) в ежедневном производстве ресторана, чтобы максимизировать его доход?

    Сначала рассмотрим ограничения. Обозначим через х₁ и х₂ соответственно количество порций мясного пирога и чизбургеров, производимых рестораном. Для их производства ресторан может ограничиться 200 кг мяса или может прикупить еще. В первом случае получаем ограничение в виде неравенства 0.25x₁ + 0.2x₂ ≤ 200, а во втором — 0.25x₁ + 0.2x₂ ≥ 200. Естественно, выбор одного из этих неравенств будет существенно влиять на возможное оптимальное решение. Так как мы не знаем, какое из них необходимо, логично заменить их одним равенством 0.25x₁ + 0.2x₂ + x₃ = 200, где x₃ — свободная переменная. Фактически свободная переменная x₃ в данной ситуации одновременно играет роль как остаточной, так и избыточной переменных.

    Далее построим целевую функцию. Ресторан хочет максимизировать свой доход. Очевидно, что для максимизации дохода желательно как можно больше продавать своей продукции, но для этого необходимы дополнительные закупки мяса. В этом случае переменная x₃ должна быть отрицательной, т.е. должна играть роль избыточной переменной.

    Для того чтобы раскрыть "двойственную" природу переменной x₃, используем стандартный математический прием, а именно представим ее в следующем виде x₃ = x₃⁺ - x₃^-, где x₃⁺, x₃^- ≥ 0.

    Если x₃⁺ > 0 и х₃^- = 0, тогда переменная x₃ играет роль остаточной.

    Если, напротив, x₃⁺ = 0 и х₃^- > 0, тогда переменная x₃ выступает в роли избыточной.

    Итак, теперь ограничение можно записать в виде равенства 0.25х₁ + 0.2х₂ + x₃⁺ - х₃^- = 200. Целевая функция получает следующее выражение.

    Максимизировать z = 0.20x₁ + 0.15х₂ - 0.25 х₃^-